Agullas, número pi e lonxitude das curvas

1990/03/01 Duoandikoetxea Zuazo, Javier - EHUko matematika irakaslea Iturria: Elhuyar aldizkaria

• Matematika

Conta de Buffon.

XVIII. No século XVIII o conde de Buffon era responsable do Xardín Real de París e aos poucos escribiu os seus vinte e cinco tomos do seu “Histoire Naturelle”. Nesa historia pensaba facer una recompilación sistemática de todos os seres vivos e cría que o ser humano debía ser o seu lugar. O principal trazo dos seres humanos é o medo á morte, segundo Buffon, pero non sabemos como decidiu que outros animais non teñen ese medo. O segundo trazo, e o que a nós nos importa aquí, é a paixón polo xogo e a iso dedicou o apartado “Essai d’Arithmétique morale”

Nos xogos xogábase diñeiro, por suposto, e temos que coñecer a nosa probabilidade de gañar para que o xogo sexa limpo. Paira pór un exemplo, supoñamos que ao lanzar un dato situámonos a favor de que apareza o número “5”. Si gañamos, débennos entregar o diñeiro xogado seis veces, xa que a probabilidade é de 1/6. Pola contra, si situámonos a favor da aparición dun número ba-coiti, só recibiremos o dobre do diñeiro xogado, porque agora a probabilidade é 1/2. Paira calcular a probabilidade, contamos os casos posibles (seis no noso exemplo) e os favorables (un no caso do “5”, tres no caso dos impares) e dividimos este último entre o primeiro.

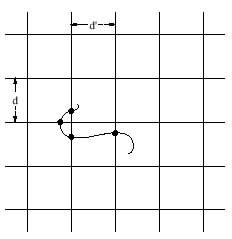
Buffon propuxo un xogo xeométrico no que o cálculo da probabilidade non se podía realizar contando casos. O “problema da agulla de Buffon” consiste en realizar unhas rectas paralelas no chan, fixando a distancia (d) entre elas e lanzando una agulla de l. de lonxitude entre elas, sendo l d. O que fai una postura a favor de que a agulla corte una liña, canto ten que recibir? Como se indicou anteriormente, é necesario coñecer a probabilidade deste suceso e concretamente obtense 2 l / d (cadro de visión). Por exemplo, se a distancia entre liñas é de 5 cm e a agulla mide 3 cm, a probabilidade é de 0,38197 e por cada peseta xogada habería que cobrar 2,618 ao acerto.

Non sabemos si este xogo utilizouse algunha vez paira gañar (ou perder) moedas, pero Laplace no seu libro “ Théorie analytique deas Probabilités ” (1812) atopou una aplicación curiosa que lle achegaba ao valor de p. Paira iso, tras tirar a agulla entre varias liñas, dividindo o número de veces que corta una liña polo número total de veces que botamos, o valor aproximado da probabilidade é tanto máis fiable canto máis se estea actuando. O valor obtido pode ser liberado por 2 l / d iguais. Os resultados que aparecen na literatura son demasiado bos paira ser cribles, pero hai que ter en conta que o que estaba a facer o experimento xa sabía o resultado que quería conseguir e cando lle conviña parábase. Se o valor de descoñécese realmente, cos tiros que se citan ao redor dos 5000 o segundo decimal sería incerto.

Pode proporse algunhas modificacións deste problema e Laplace propuxo una formulación máis xeral: o plano divídese agora en cadros, con rectas paralelas horizontais a unha distancia d’ e verticais a unha distancia d’, e entre elas lánzase un fío de lonxitude l, de calquera forma (non necesariamente directa como a agulla). O fío pode cortar a rede de liñas en varios puntos e a esperanza matemática do número de puntos de corte é:

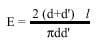
É dicir, si tras o lanzamento N o número medio de puntos de corte é E(N), cando N vai cara ao infinito, E(N) vai cara ao valor de E superior. Como se pode observar, cando d’ vai cara ao infinito obtense o resultado da antiga agulla de Buffon. E una vez máis, coñecendo d, d’ e l, esta fórmula pódese utilizar paira achegarse ao número.

Se non resulta interesante paira o cálculo desta vía, nesta nova formulación existe un valor que pode ser realmente descoñecido, é dicir, a lonxitude do fío. E parece que na práctica tamén se utilizou. Se miramos ao microscopio, é posible que algunhas das lonxitudes que aparecen nel non poidan medirse. Non podemos tirar o “fío” ao plano cuadri-culto, pero podemos proxectar sobre a imaxe do microscopio una malla cuadriculada (coñecendo as diferenzas) e contar os puntos de corte, virar a rede e volver contar os cortes até completar a xira. O número medio de cortes dános un valor aproximado da E superior e coa súa fórmula obtense a lonxitude, loxicamente porque coñecemos o valor de.

A parte das Matemáticas que estuda estes problemas e outros similares chámase “Probabilidade Xeométrica”. O primeiro volume da colección “Integral Geometry and Geometric Probability” (“Encyclopedia of Mathematics and its Applications”, Addison-Wesley, 1976) de Santaló descubrirá cousas interesantes sobre este tema. No prólogo do libro, o prestixioso matemático Mark Kac cualifica ao profesor Santaló como “o xefe indiscutible de Xeometría Integral durante moitos anos”.