Aiguilles, nombre pi et longueur des courbes

1990/03/01 Duoandikoetxea Zuazo, Javier - EHUko matematika irakaslea Iturria: Elhuyar aldizkaria

• Matematika

Compte Buffon.

XVIII. Au XVIIIe siècle, le comte de Buffon était responsable du Jardin Royal de Paris et écrivit peu à peu ses vingt-cinq volumes de son «Histoire Naturelle». Dans cette histoire, il pensait faire une compilation systématique de tous les êtres vivants et croyait que l'être humain devait être sa place. Le principal trait des êtres humains est la peur de la mort, selon Buffon, mais nous ne savons pas comment il a décidé que d'autres animaux n'ont pas cette peur. Le deuxième trait, et ce qui nous importe ici, est la passion pour le jeu et c’est à cela qu’il a consacré la section “Essai d’Arithmétique morale”

Dans les jeux, nous avons joué de l'argent, bien sûr, et nous devons connaître notre chance de gagner pour rendre le jeu propre. Pour donner un exemple, supposons qu’en lançant une donnée, nous nous positionnons en faveur de l’affichage du numéro « 5 ». Si nous gagnons, nous devons livrer l'argent joué six fois, car la probabilité est de 1/6. Au contraire, si nous nous positionnons en faveur de l'apparition d'un nombre ba-coiti, nous ne recevrons que le double de l'argent joué, car maintenant la probabilité est 1/2. Pour calculer la probabilité, nous comptons les cas possibles (six dans notre exemple) et les cas favorables (un dans le cas du “5”, trois dans le cas des impairs) et divisons ce dernier entre le premier.

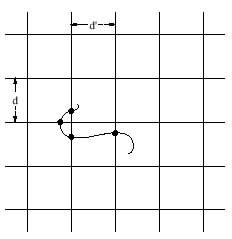
Buffon a proposé un jeu géométrique dans lequel le calcul de probabilité ne pouvait pas être fait en comptant des cas. Le « problème de l'aiguille de Buffon » consiste à réaliser des droites parallèles dans le sol, en fixant la distance (d) entre elles et en lançant une aiguille de l. de longueur entre elles, étant l. d. Celui qui fait une posture pour que l'aiguille coupe une ligne, combien doit-il recevoir? Comme indiqué ci-dessus, il est nécessaire de connaître la probabilité de cet événement et concrètement vous obtenez 2 l / d (boîte de vision). Par exemple, si la distance entre les lignes est de 5 cm et que l'aiguille mesure 3 cm, la probabilité est de 0,38197 et pour chaque peseta jouée, il faudrait charger 2,618 à la bonne.

Nous ne savons pas si ce jeu a déjà été utilisé pour gagner (ou perdre) des pièces, mais Laplace dans son livre “ Théorie analytique des probabilités ” (1812) a trouvé une application curieuse qui l'approchait de la valeur de p. Pour ce faire, après avoir tiré l'aiguille entre plusieurs lignes, divisant le nombre de fois que vous coupez une ligne par le nombre total de fois que vous avez lancé, la valeur approximative de la probabilité est d'autant plus fiable que vous agissez. La valeur obtenue peut être libérée par 2 l / d égaux. Les résultats qui apparaissent dans la littérature sont trop bons pour être crédibles, mais il faut garder à l'esprit que celui qui faisait l'expérience savait déjà le résultat qu'il voulait obtenir et quand il lui convenait il s'arrêtait. Si la valeur est vraiment inconnue, avec les tirs cités autour de 5000 le second décimal serait incertain.

On peut proposer quelques modifications de ce problème et Laplace proposa une formulation plus générale: le plan est maintenant divisé en tableaux, avec des droites parallèles horizontales à une distance d’ et verticales à une distance d’, et entre elles on jette un fil de longueur l, de toute forme (pas nécessairement directe comme l'aiguille). Le fil peut couper le réseau de lignes en plusieurs points et l'espoir mathématique du nombre de points de coupe est:

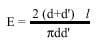
C'est-à-dire que si après le lancement N le nombre moyen de points de coupe est E(N), quand N va vers l'infini, E(N) va vers la valeur de E supérieure. Comme vous pouvez le constater, quand d’ va à l'infini vous obtenez le résultat de l'ancienne aiguille de Buffon. Et encore une fois, connaissant d, d’ et l, cette formule peut être utilisée pour approcher le nombre.

S'il n'est pas intéressant pour le calcul de cette voie, dans cette nouvelle formulation il ya une valeur qui peut être vraiment inconnu, à savoir la longueur du fil. Et il semble que dans la pratique a également été utilisé. Si nous regardons le microscope, il est possible que certaines longueurs qui y apparaissent ne puissent pas être mesurées. On ne peut pas tirer le “fil” sur le plan quadri-culte, mais on peut projeter sur l’image du microscope un maillage quadrillé (connaissant les différences) et compter les points de coupe, tourner le filet et recompter les coupes jusqu’à compléter la tournée. Le nombre moyen de coupes nous donne une valeur approximative du E supérieur et avec sa formule, vous obtenez la longueur, logiquement parce que nous connaissons la valeur de.

La partie des mathématiques qui étudie ces problèmes et d'autres semblables est appelée “Probabilité géométrique”. Le premier volume de la collection “Integral Geometry and Geometric Probability” (“Encyclopedia of Mathematics and its Applications”, Addison-Wesley, 1976) de Santaló découvrira des choses intéressantes sur ce sujet. Dans le prologue du livre, le prestigieux mathématicien Mark Kac qualifie le professeur Santaló de «chef incontesté de la géométrie intégrale pendant de nombreuses années».