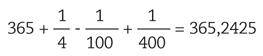Val la pena que l'any 3200 sigui bianual?

2014/01/01 Alberdi Celaya, Elisabete - Matematikan lizentziatua eta doktoregaia Iturria: Elhuyar aldizkaria

• Historia
• Matematika

Hem comptat de diferents maneres el nombre de dies que falta per a arribar a un dia concret. Fa 13.000 anys, els humans de Cro-Magnon, per a comptar els dies que hi havia entre la primera gelada d'hivern i la primavera, comptaven llunes plenes; els presos han comptat amb ratlles el nombre de dies que faltaven per a deixar la presó i ser lliures; i compten el temps que han de dormir els nens per a arribar a Olentzero. Basat en les etapes de la Lluna, amb ratlles o el nombre de duels que cal fer com a unitat, són exemples d'un calendari que tots portem penjat en la paret, damunt de la taula o guardat en el moneder.

Primer calendari: Basat en les etapes de la Lluna

A l'ésser humà li ve des de fa temps l'obsessió per mesurar el temps. En temps en els quals som capaços de mesurar nanosegons (10 -9 segons) i femtosegundos (10 -15 segons), potser ens resulta estrany el recorregut de l'home a la recerca d'un calendari concret, però així ha estat: el calendari concret i útil ha estat durant molt de temps un dels reptes més importants de l'ésser humà.

Encara que no tots els calendaris de temps antics funcionen de la mateixa manera, sí que tenen diverses característiques comunes. Per exemple, la majoria dels calendaris són cíclics, és a dir, una vegada complert un període, es repeteixen. La majoria d'elles s'expressen de forma circular, ja que en les cultures d'antany representaven al firmament com a disc, cercle o esfera. Aquesta esfera es dividia en mesos lunars o de sol i el cel es distribuïa en 360 dies a l'any o 360 graus.

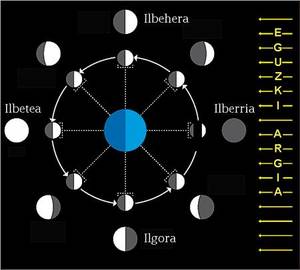
Els astrònoms de l'Edat de Pedra van observar els períodes de la Lluna, ja que es van adonar que podien comptar les nits entre els moments de la Lluna plena, semillena i totalment fosca, i que es repetien. Així, alguns antropòlegs consideren que el calendari dels primers que va utilitzar l'ésser humà és el format per diverses osques realitzades en un os d'àguila, formades per una impressió regular de diferents agrupacions de símbols similars.

La lluna necessita uns 29 dies i mig (29,5306 dies) per a passar de la lluna a la lluna creixent, de la lluna creixent a la lluna plena, de la lluna en quart minvant i de la lluna en quart minvant. Dotze cicles complets de la Lluna cobreixen aproximadament les quatre estacions de l'any, que conformaven el que les societats de llavors ja coneixien com un any. Grecs, jueus, xinesos... van utilitzar l'any lunar, compost per 12 mesos de 29 dies i mig, amb un total de 354 dies.

No obstant això, els que disposaven d'un calendari basat en els períodes lunars no van trigar molt a adonar-se que el seu any tenia algun error, ja que en el seu calendari són 8 anys suficients perquè el començament de la primavera es produís a principis de l'estiu del seu calendari, i així, en 16 anys, el començament de l'estiu coincidia amb el començament de l'hivern. Per a corregir l'error detectat l'any lunar, els grecs afegien 90 dies en el seu calendari cada 8 anys, els jueus afegien un mes lunar cada 3 anys i els matemàtics xinesos deien que cada 19 anys calia afegir 7 mesos lunars.

De la lluna a l'any solar

Sumer a. C. XXI. En el segle XX estàvem en un any de 360 dies, conseqüència de l'arrodoniment del mes lunar a 30 dies. El sistema sumeri es basava en els números 6 i 60. La multiplicació de tots dos números dóna 360, i aquest número continua sent el que utilitzem per a distribuir el cimaci o qualsevol pla circular. Els Babilonis van heretar el sistema de numeració dels sumeris i van repartir el dia 24 hores. Encara que no se sap el perquè, sembla que és un número relacionat amb el zodíac i que li va portar les seves creences astrológicas.

L'any solar és la durada del moviment de translació de la Terra al voltant del Sol, que comprèn 365,242190 dies. Fa uns 6.000 anys, l'egipci va corregir l'error de l'any lunar i va prendre l'any solar la primera civilització. El seu calendari tenia 12 mesos de 30 dies i 5 dies addicionals. Aquests cinc dies addicionals es van convertir en dies de déus Osiris, Isis, Horus, Neftis i Set. Si bé és un misteri com els egipcis van fer tan bona aproximació a l'any solar, l'explicació més creïble la trobem en el riu Nil: Des de finals de juny fins a finals d'octubre es produïen inundacions en el riu Nil, que deixava un bon sòl per a la collita des d'octubre a febrer, per la qual cosa des de febrer fins a finals de juny es recollia una abundant collita en els terrenys confrontants al riu. Per tant, els habitants de la zona només havien de comptar els dies entre una inundació i la següent per a calcular la durada de l'any solar. Els astrònoms egipcis també es van adonar que l'any solar era un quart de dia més llarg del calendari que ells mateixos tenien, i que l'any C. L'any 238 la durada de l'any solar es va establir en 365 1/4 dies.

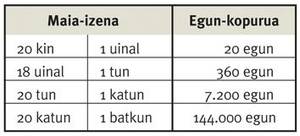
Però els egipcis no van ser els únics que van utilitzar el calendari de 365 dies. Els maies van utilitzar 3 sistemes de calendari, en un dels quals la durada de l'any era de 365 dies. Un dels calendaris utilitzats pels maies és l'anomenat calendari civil ( haab ), el segon és l'anomenat calendari sagrat ( tzolkin ) i el tercer és l'anomenat relat llarg. El calendari Haab té 18 mesos de 20 dies i un mes de 5 dies, amb un total de 365 dies. Sembla que els maies també sabien que la durada de l'any era de 365 1/4 dies, encara que en el seu calendari no tenien en compte el quart de dia. El calendari de Tzolkin té 260 dies i el sistema de compte llarg es basa en unitats de 360 dies, utilitzant la unitat tun i el número 20. Per a ells el batkun és un interval de temps de 144.000 dies, i multiplicant el batkun per 13 aconsegueixen el que es denomina cicle llarg, amb una durada aproximada de 5.130 anys. Ells creien que, després d'un llarg cicle, fins llavors desapareixia, donant pas a un nou món. El 21 de desembre de 2012 finalitza el seu últim cicle, a. C. Iniciat cap al 3114. Encara que no se sap amb certesa, els maies van donar la longitud del seu any basant-se en observacions astronòmiques.

El nostre calendari: calendari gregorià

En l'actualitat, el calendari que utilitzem en la major part del món és gregorià, el XVI. Implantat en el segle XVIII pel Papa Gregori XIII. El seu objectiu era que la durada de l'any d'aquest calendari fos el més semblant possible a la de l'any solar. El calendari gregorià és el calendari solar: Compost per 365 dies i 12 mesos, que inclou un dia addicional en els biennis. Un any és biaño quan és múltiple de quatre números. L'excepció són els anys que són múltiples de 100, que són només bisaños quan són múltiples de 400. Per exemple, 1700., Els anys 1800 i 1900 no són anys de traspàs, però el 2000 és biaño. Calendaris gregorians Juli Cèsar. Va substituir al calendari julià establert l'any 45. La principal diferència entre ells és que en el calendari julià tots els anys eren múltiples del número 4. L'any del calendari julià tenia una mitjana de 365,25 dies. En el calendari gregorià, per contra, al no ser 3 anys de 4 a 3 anys múltiples de 100, en un cicle de 400 anys, en comptes de 100 anys, hi ha 97 anys de visats, la qual cosa suposa 400 x 365 + 97 = 146.097 dies. Això ens dóna un any de 146.097/400 = 365,2425 dies de durada mitjana. Per tant, el calendari gregorià s'acosta millor a l'any solar que el calendari julià.

Cap als 1.600 anys que portava el calendari julià tenia un error acumulat d'uns 10 dies respecte al calendari gregorià (i també respecte a l'any solar), és a dir, 10 dies després. Per a esmenar aquest error, quan es va establir el calendari gregorià, al 4 d'octubre de 1582 del calendari julià, va seguir el 15 d'octubre de 1582 del calendari gregorià. Els països catòlics, com Espanya, Portugal i Itàlia, van aprovar immediatament el calendari gregorià.

No obstant això, el calendari gregorià tampoc dóna una durada exacta de l'any solar, amb una diferència de 3,1·10 -4 dies. És a dir, el calendari gregorià introdueix un dia addicional a l'any solar cada 3.225 anys aproximadament. Podem pensar en un altre calendari que redueixi l'error d'aquest calendari?

La durada del calendari gregorià pot calcular-se de la següent manera:

Atès que l'any del calendari gregorià és més llarg que l'any solar, per exemple, es poden llevar alguns anys de visat perquè s'acosti més a la durada de l'any solar. Per exemple, si restem la condició de bisaño als múltiples de 3.200, la durada de l'any seria:

És a dir, si el bisaño és múltiple de 4, però només és múltiple de 100 si és múltiple de 400, però no és múltiple de 3.200, tenim un calendari que s'acosta millor a l'any solar. No és estrany que aparegui el número 3.200, ja que, com s'ha dit anteriorment, el calendari gregorià inclou un dia addicional cada 3.225 anys.

Per a acabar...

En el calendari gregorià, enguany és 2014; en el calendari coreà, el 4347a; en el calendari maia, el 2n any del nou període; en el xinès, l'any del cavall... L'objectiu de tots és acostar-nos el màxim possible a l'any solar. Si l'any solar fos un número normal, tot seria més fàcil i no necessitaríem visats. A pesar que cada 3.200 anys es millora la precisió del calendari gregorià eliminant un dia, no és necessari fer-lo, ja que en aquest període no hi ha res a ficar un error d'un dia, i en aquest període es modifiquen els cicles del Sol, la Terra, etc.

No serem els que modificarem el calendari gregorià que no ha sofert canvis des que nosaltres l'havíem establert, deixarem de treballar els canvis de cicle. Qui sap, potser la durada de l'any solar passa a ser de 365 dies concrets, la qual cosa facilitarà les tasques d'elaboració del calendari.

Bibliografia