Ayudante de Matemáticas

2000/04/01 Duoandikoetxea Zuazo, Javier - EHUko matematika irakaslea Iturria: Elhuyar aldizkaria

• Matematika

Johann Radon (1887-1956) e idea matemática

Johann Radon nació en 1887 en Tetschen (Bohemia), actualmente Decin, República Checa. Estudió Matemáticas en la Universidad de Viena y, tras ser profesor en varias universidades alemanas, regresó a Viena en 1947, donde falleció como profesor en 1956. Es conocido por los matemáticos, que abandonó importantes trabajos, especialmente en la teoría de la integración.

A pesar de que no es tan conocido, el resultado que sustenta la tomografía se sitúa en Radón, precedido por un artículo de 1917. En términos técnicos, una versión del hermoso teorema de Radón podría expresarse como: una función dada en el plano puede recuperarse mediante integrales (unidimensional) realizadas sobre todas las rectas. Y conociendo estas integrales, también dio una fórmula para recuperar la función. Sin asustar más al lector que se siente perdido entre estos términos matemáticos, veremos un ejemplo sencillo.

Supongamos que en el plano tenemos un conjunto cerrado con dos orificios en su interior, como muestra la imagen. Estando fuera del plano y mirando sin obstáculos, como haces al leer esta página, no tienes problemas para ver los agujeros interiores. Pero la hormiga que vive sobre el papel y no puede levantar la cabeza del papel sólo puede describir el límite exterior que rodea al conjunto. ¿Cómo sabrá que dentro hay dos agujeros? De la misma manera, si hubiera una pared en el límite exterior del conjunto, nuestros ojos no podrían ver la parte interior y estaríamos en el mismo estado de la hormiga, conociendo la arista, pero sin información alguna del interior. ¿En qué consiste el teorema de Radón? "Si me da la longitud que da cada línea recta al cortar el conjunto, os voy a definir completamente el conjunto" nos dice Radón, ya que permite describir todos los límites exteriores e interiores. (Tomando sobre el conjunto una función que vale 1 y fuera y 0 en los orificios, la integral sobre una recta es la longitud indicada.) Hemos modificado el problema, ahora necesitaríamos longitudes de corte, pero parece que para calcular las longitudes hay que conocer el interior. ¿Estamos en una rueda loca?

Allan Cormack (1924-1998) y la solución teórica

Allan Cormack nació en Johannesburgo (Sudáfrica) en 1924, hijo de funcionarios escoceses. Empezó sus estudios de Ingeniería en la Universidad de la Ciudad del Cabo, pero finalmente decidió cambiar a Física. Durante su tesis doctoral en el prestigioso Laboratorio Cavendish de Cambridge, estudió una oferta universitaria y regresó a Sudáfrica antes de finalizar la tesis. Años más tarde se trasladó a la Universidad de Harvard para realizar la investigación y finalmente quedó en Estados Unidos como profesor e investigador de la Universidad de Tufts (Massachussets).

Según él, aunque el interés por desarrollar la tomografía computarizada se despertó durante su estancia en Sudáfrica, tuvo que trabajar en América la Física nuclear y la Física de Partículas, y sólo ocasionalmente tuvo ocasión de analizar el problema de la tomografía. Sin embargo, su trabajo fue fructífero y expuso en dos artículos publicados en 1963 y 1964 la base teórica de la tomografía.

Mira una parte de tu cuerpo, como la rodilla. Lo ves desde fuera, pero no desde dentro. Supongamos que un plano imaginario te atraviesa la rodilla y estás en la misma situación que el ejemplo del apartado anterior, es decir, el corte genera una imagen plana y sólo ves la línea exterior, no sabes cuál es la estructura interna. ¡Si pudiéramos calcular "integrales"! Cormack pronto entendió que se trataba de un problema matemático que ganaría si se consiguiera una vía práctica de cálculo. Encontró respuesta en rayos X.

Los rayos X fueron descubiertos por Röntgen en 1895 y se consideró un tipo de radiación electromagnética de menor longitud de onda que la luz. Dada su propiedad de atravesar varios objetos opacos a la luz, se detectó la posibilidad de obtener unas "fotos" especiales que dieron lugar a las radiografías tan utilizadas por los médicos. Pero al igual que ocurre en las fotos, los objetos que se encuentran en distintos planos deberían aparecer entre sí en las radiografías, por lo que la anterior oculta la posterior. La técnica de la tomografía es completamente diferente, ya que, como su propio nombre indica, cada imagen muestra un corte (tómos, griego), evitando superposiciones.

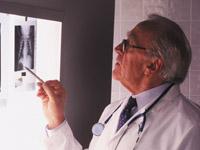
Los rayos X se propagan en líneas rectas y pierden intensidad en el camino. Siendo esta pérdida proporcional a la intensidad, longitud del recorrido y densidad del medio, una ecuación matemática nos indica que para obtener la integral de la densidad basta con conocer las intensidades de entrada y salida. Como las mediciones se realizan en el exterior, Cormack nos ha inventado un camino que haría posible la integral que pedíamos más arriba sin ver el interior. A partir de ahí la Matemática necesitaba más inversión para conocer la función o para hacer la imagen de una manera más práctica. Además, en el mundo real no es posible realizar todas las integrales que exige la teoría, ya que aparecen infinitos integrales y los métodos de aproximación también deben ser solicitados a las Matemáticas.

Ante la evidente revolución que podía suponer la propuesta de Cormack, ¿por qué no se llevó a cabo inmediatamente y se construyó una herramienta que hiciera imágenes? No hay respuestas claras, pero parece que la capacidad de los ordenadores de entonces no era suficiente para realizar todos los cálculos necesarios. Por ello, tras la publicación de los artículos, Cormack abandonó el tema para retomarlo cuando diez años más tarde su invento se hizo realidad.

Godfrey Hounsfield (1919) y primeras máquinas

Godfrey Hounsfield nació en el condado inglés de Nottinghamshire en 1919. La Segunda Guerra Mundial se celebró en el Ejército del Aire, sobre todo en radares y radiocomunicaciones. Tras la guerra estudió Ingeniería eléctrica en Londres y en 1951 se incorporó a la empresa EMI (Electric and Musical Industries), conocida para nosotros como discográfica. A pesar de los inicios de los ordenadores, Hounsfield pronto se propuso al respecto y en 1958 construyó el primer ordenador británico en transistor con su equipo (EMIDEC 1100).

Años más tarde, tras inviabilidad de un proyecto en el que trabajaba, le dieron libertad para estudiar nuevos campos y propuso trabajar el reconocimiento automático de formas. En esta línea, desarrolló la idea básica de la OTA en 1967 y la patentó al año siguiente. Cuatro años después se construyó la primera máquina (EMI-Scanner).

Como se ha mencionado anteriormente, en la práctica no es posible realizar mediciones (es decir, “integrales”) sobre todas las rectas. Seleccionando algunas direcciones de un plano y emitiendo rayos paralelos, se mide la intensidad mediante unos sensores de cristal situados al otro lado. Los datos obtenidos son tomados por el ordenador y, resolviendo un montón de ecuaciones, ofrece una imagen aproximada de la intersección del plano sobre el cuerpo. El proceso se repite con un poco de movimiento del plano y finalmente se aprecia la estructura interna del cuerpo mediante la visualización de imágenes de cortes sucesivos. Lo que hemos dicho en pocas palabras supone superar muchos obstáculos teóricos y prácticos para que la imagen que da la máquina sea fiable. Además del conocimiento técnico, Hounsfield es un reconocimiento a la imaginación y a la intuición. Sin utilizar los métodos de las matemáticas y la capacidad de cálculo de los ordenadores no hubiera sido posible encauzar este invento.

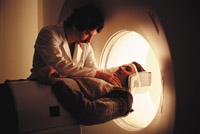
Allan Cormack y Godfrey Hounsfield consiguieron el Premio Nobel de Medicina y Fisiología de 1979 por su posible tomografía computarizada. A partir de entonces la técnica ha ido evolucionando y las herramientas han mejorado; si inicialmente se utilizaban rayos paralelos, ahora se emiten haces de rayos desde varios puntos. Por otra parte, el crecimiento de la capacidad de cálculo de los ordenadores ha sido también positivo. Esto nos lleva a pensar que cada vez con medidas en más líneas rectas se consigue una mejor imagen. Sin embargo, la práctica tiene un límite: la salud de los seres vivos. No se pueden hacer circular rayos a través del cuerpo, ya que existe el riesgo de causar grandes daños. En cualquier caso, la OTA ha obtenido un gran éxito y se utiliza de forma masiva, no sólo en el ámbito médico.