Jeux sur Lotus

1986/08/01 Goñi, Jesus Mari | Etxeberria, J. Iturria: Elhuyar aldizkaria

• Matematika

Comme Alice nous est allé en vacances, cette fois sera un autre type de jeu le thème de notre travail.

Ces derniers mois, nous avons vu le début de l'implantation du jeu des lotus dans l'État. Dès le départ, les gens l'ont accepté avec beaucoup d'espoir. Magazines, journaux… et autres publications sont pleines d'articles sur le lotus.

Ces articles et paragraphes parlent d'un système court, et bien qu'il ne soit pas dit exactement, il s'agit de convaincre les parieurs qu'il existe différentes façons de remplir ces billets, et que les numéros qui vont sortir sont facilement accessibles.

Lotus est un jeu de hasard (aléatoire) et les nombres qui vont sortir il n'y a aucun moyen approprié de prédire.

Cela dit, nous ne vous donnerons pas la bonne voie pour rapprocher les nombres et... de toute façon, même si nous avons ce chemin, nous ne vous l'expliquerons pas. Comprenez-vous pourquoi ?

Cependant, nous voulons faire quelques petites études sur le lotus. Tout d'abord, quelle probabilité avons-nous d'inventer les six numéros lorsque nous jouons cinq vingt et un?

Comme nous le savons, la définition classique de probabilité fournit la probabilité d'un événement A comme suit:

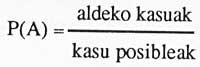
Dans notre pari, les six cas favorables sont un. Et… combien de cas sont possibles ?

Le problème n'est pas difficile, car nous savons que sur les 49 numéros vous devez choisir six et les six.

Et les cas possibles de sortie des six numéros différents seront obtenus: Combiner des groupes de 6 à 6 avec ces 49 numéros. Autrement dit, dans un ensemble numérique de 49, tous les sous-groupes numériques 6 seront :

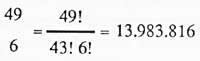
Par conséquent, la probabilité de succès est:

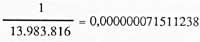
Il ne nous est pas sorti très grand, non? Mais si nous prenons 200 millions ? Eh bien, nous sommes tous des adultes et chacun le verra.

Lors de la réalisation de nos calculs, nous devrions noter que le système de loterie de Loto est le même que celui de Noël. Mais si 100 000 numéros sont distribués à Noël, 13.983.816 sont distribués à Loto. Ce qui change, c'est bien sûr la remise des prix.

Et nous n'avons jamais vu les systèmes abrégés qui parlent toujours de la loterie de Noël !

Puisque nous avons commencé à parler de Loto, nous voulons vous proposer quelques casse-tête sur ce jeu.

Ces casse-tête sont ceux réalisés après une conversation au bar.

Là, je discutais plusieurs enfants et pour la première fois, nous avons entendu:

Je ne sais pas comment j'ai rempli cette carte de lotus, mais la semaine dernière, je n'ai pas inventé... Puis c'est difficile ! Je ne sais pas pourquoi ils ne décernent pas de prix dans ces cas.

(1) Nous: Quelle est la probabilité qu'aucun nombre invente?

Pello dit: Je pense que les nombres pairs sortent plus. Regardez la semaine dernière, cinq des six numéros étaient paires... La semaine prochaine je dois mettre toutes les paires.

(2) Nous: Quelle est la probabilité que les six nombres soient pairs ?

Le serveur a également participé et dit:

La vérité est que les chiffres se terminent en chiffres différents. Si nous prenons ceux de la semaine précédente: Ils ont terminé avec 2, 6, 3, 4, 0 et 8.

Nous: Quelle est la probabilité que les 6 chiffres se terminent par des chiffres différents?

Comme nous le voyons, tout le monde avait quelque chose à dire. Joseph arriva alors et il nous jeta ce qui suit.

En deux semaines consécutives, au moins un nombre est répété.

(4) Nous: Quelle est la probabilité que se produise ce que Joxe a dit ?

(5) Nous vous avons finalement expliqué ce problème. Vous devez choisir 6 numéros, mais compte tenu des conditions suivantes, et bien sûr, vous avez cinq vingt et un numéros.

• Pas de numéro premier (cousins)
• Lorsque vous choisissez 6 numéros de Loto, utiliser 10 chiffres et utiliser chaque chiffre au maximum une fois.
• Une fois un numéro sélectionné, vous ne pouvez pas le mettre dans vos cases adjacentes.
• La dernière condition peut être comprise de deux façons.

Si les "cases contiguës" sont d'un côté commun, nous avons obtenu 6 résolutions.

Si les cases adjacentes sont celles qui ont un point commun, nous avons obtenu une seule résolution.

Eh bien, maintenant il reste entre vos mains... Ah ! et dépenser peu!