Games about Lotus

1986/08/01 Goñi, Jesus Mari | Etxeberria, J. Iturria: Elhuyar aldizkaria

• Matematika

As Alicia has gone on vacation, this time it will be another type of game the theme of our work.

In recent months we have seen the beginning of the implementation of the lotus game in the State. Just get it going, people have accepted it with great hope. Magazines, newspapers… and other publications are full of lotus articles.

These articles and sections speak of a short system, and although not exactly said, it is a matter of convincing the bettors that there are different ways to fill those tickets, and that the numbers that will come out are easily accessible.

Lotus is a game of chance (random) and the numbers that will come out there is no proper way to predict.

Having said this, we will not give you the right way to correct the numbers and... anyway, even if we have that way, we would not explain it to you. Do you understand why?

However, we want to do some small studies on the lotus. First, how likely are we to invent the six numbers when we play five twenty-one?

As we know, the classical definition of probability provides the probability of an A event as follows:

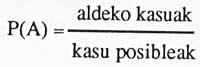
In our bet, the six favorable cases are one. And how many cases are possible?

The problem is not difficult, because we know that of the 49 numbers you have to choose six and hit the six.

And the possible exit cases of the six different numbers will be obtained: Combining groups of 6 in 6 with these 49 numbers. That is, in a numerical set of 49, all numerical subgroups 6 will be:

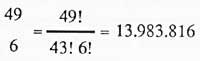
Therefore, the probability of success is:

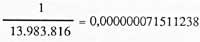
It hasn't come out very big, hasn't it? But, however, if we assume 200 million? Well, we are all adults and everyone will see it.

When performing our calculations we should take into account that the lottery system of Lotus lottery is the same as that of Christmas. But if at Christmas 100,000 numbers are distributed, 13.983.816 is distributed in Loto. What changes is, of course, the award ceremony.

And we have never seen the shortened systems that still speak of the Christmas lottery!

Since we have started talking about Lotus, we want to propose some headaches about this game.

These headaches are made after a conversation at the bar.

There I was chatting several children and for the first time we heard:

I don't know how I filled this lotus card, but last week I didn't invent any numbers... then it is difficult! I don't know why they don't award prizes in these cases.

(1) We: What is the probability that no number will invent?

Pello said: I think even numbers come out more. Look last week, five of the six numbers were even... Next week I have to put all pairs.

(2) We: What is the probability that the six numbers are even?

The server also participated and said:

The truth is that the numbers end in different figures. If we take those of the previous week: They finished with 2, 6, 3, 4, 0 and 8.

We: What is the probability of the 6 numbers ending with different figures?

As we see, everyone had something to say. Joseph came then and he threw us the following.

In two consecutive weeks, at least one number is repeated.

(4) We: What is the probability of what Joxe has said?

(5) Finally we explain this problem to you. You have to choose 6 numbers, but considering the following conditions, and of course, you have five twenty-one numbers.

• No number first (cousins)
• When choosing 6 Lotus numbers, use 10 figures and use each figure at most once.
• Once a number is selected, you cannot put it in its adjacent boxes.
• The last condition can be understood in two ways.

If the "contiguous boxes" are on a common side, we have obtained 6 resolutions.

If the adjacent boxes are those with a common point, we have obtained a single resolution.

Well, now it's in your hands... Ah! and spend little!