Kontroladoreen historia

Azken finean, robota gidatzeko behar den kontrol-teknika ezaguna da aspaldidanik eta prozesu industrial anitzetan topa daiteke.

1. irudi. Antzina egiten zen fluxu eta jariakin-mailen kontrola (ezkerrean) eta egungo komunetako dispositibo baten eskema eskuinean.

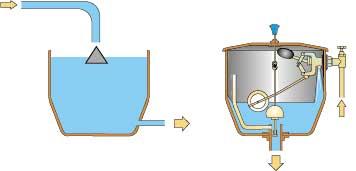
Urteetan zehar agertu diren kontrolagailuen azterketa egiten hasiz gero, antzinatik datozen elementuak topatzen dira. Horrela, XVII. mendera arte, olio-lanpara baten likido-maila kontrolatzeko edo ardo-ontzi baten maila mantentzeko sistemak (nahiz eta edalontzi asko bete), kontrol-sistemak dira. Horrelako sistemetan fluxua kontrolatzeko jariakinaren maila kontrolatzen da, zulo batetik igarotzen den fluxua presioarekiko proportzionala delako. Jariakin-maila kontrolatzeko antzina asmatu zuten tresna, komunetako depositoetan oraindik ere erabiltzen den flotagailua da. Jariakin-maila txikitzen den neurrian, elikadura-fluxua handiago egiten da eta maila handitzen denean, elikadura-fluxua murrizten da, behar den kasuan fluxu hori deuseztuz. 1. irudian tresna honen aurkezpena eta gaur egungo komunetako deposito baten eskema ikusten da. Sistema honetan, sentsorea eta eragingailua dispositibo bakarrean (flotagailua eta elikadura-hodia) konbinatuta daude.

XVII. eta XIX. mendeen artean agertutako lanetako bat, Drebbel-ek (1620) eta txita-inkubagailua berotzeko diseinatutako labeko tenperatura-kontrola da. 2. irudian kontrol honen diseinua aurkezten da. Sua barnean duen kutxa eta tiro-erreguladorea duen hodi batez osatuta dago labea. Errekuntza-ganbararen barruan horma bikoitzak dituen txita-inkubagailua aurki daiteke, eta horma horien arteko tartea urez betetzen da. Tenperatura-sentsorea aipatutako tartean kokatuta dagoen alkoholez eta merkurioz betetako beirazko ontzia da.

Suak kutxa eta ura berotzen dituen heinean, alkohola dilatatu eta flotagailua daraman zurtoinak gorantz egiten du, tiro-erreguladorea hodirantz jaitsiaraziz. Kutxa hotzegia dagoenean, alkoholaren bolumena murriztu egiten da eta erreguladorea ireki eta suaren indarra handitzen da. Lortu nahi den tenperatura, flotagailua daraman zurtoinaren luzerak ematen du.

Garai horretan bertan, ardatzen errotazio-abiadura kontrolatzea premiazko arazoa zen kontrol automatikoaren arloan. Adibidez, garia ehotzen duen haize-errota baten harriaren abiaduraren kontrola, kontrol automatikoa da. Erabili ziren metodo desberdinen artean, pendulu konikoa edo bola-erreguladorean oinarritutakoa izan zen hoberena. Dispositibo hau errotaren abiadura neurtzeko erabiltzen zen. Baina aipatutako erreguladore-mota hau famatua egin zuen aplikazioa lurrin-makinarena izan zen (Watt, 1788). 3. irudian makina honen argazkia eta eskema agertzen da eta 4. irudian bola higikorreko erreguladorearen lehen planoa.

Erreguladore zentrifugoaren ekintza oso erraz uler daiteke. Demagun makinari bere oreka-egoeran lanean egonik, bat-batean karga aplikatzen zaiola. Une horretan, makinaren abiadura murriztu eta erreguladorearen bolek osatzen duten konoa txikitu egiten da. Horrela, bolek bertikalarekin osatzen duten angelua irteerako sentsore bezala erabiltzen da. Ekintza honek, lurrinaren balbula nagusia (eragingailua) ireki eta lurrin gehiago pasaraziko du makinarantz, galdu den abiadura berreskuratzearren. Lurrin-balbula egoera horretan mantentzeko, erreguladorearen bolek angelu ezberdina osatu beharko dute eta, ondorioz, karga aplikatu ondoren lortutako abiadura ez da aurrekoaren berdin-berdina izango.

3. irudia. Watt-en lurrin-makinaren argazkia eta eskema.

Watt injineru praktikoa izan zen, bere aurretik haize-errotekin lan egin zuen hura bezala, eta erreguladorearen analisi teorikorik ez zuen egin. XIX. mendearen azken aldera, aipatutako kontrol-sistemaren ikerketak praktika hutsa izatetik analisi teorikoen muin izatera pasa ziren. G.B. Airy matematika eta astronomiako irakasle izan zen Cambridge-ko Unibertsitatean 1826-35 bitartean eta Greenwich-eko astronomoa 1835-81 bitartean. Airy-k abiaduraren inguruko ikerketa ugari egin ondoren, penduluaren erreguladoreak mugimendu desegonkorra izan zezakeela aurkitu zuen. Airy-rena da kontrol-sistema baten desegonkortasunaren lehen analisia. Analisia ekuazio diferentzialetan oinarrituta egonik, berrelikadura-kontrolaren analisiaren hasiera izan zen.

Berrelikadura-kontroleko egonkortasunaren lehen lan sistematikoa, Maxwell-en (1868) “On Governos” lana izan zen. Lan honetan, Maxwell-ek erreguladorearen ekuazio diferentzialak garatu zituen, oreka-puntuaren inguruan linealizatuz. Era honetan, egonkortasuna ekuazio baten erroei lotuta dagoela frogatu zuen; hau da, aipatutako erroek zati erreal negatiboak izan behar zituztela, hain zuzen ere.

Egonkortasun-irizpidearen arazoa, 1877. urteko Adams saria irabazi zuen E.J. Routh-ek konpondu zuela ikus daiteke. Saria irabazteko balio izan zuen entsaioan garatutako irizpidea, kontrol-injineruek oraindik ere ikasten duten teknika da. Ekuazio karakteristikoaren analisia kontrol-teoriaren oinarri izaten jarraitu zuen Bell Telephone-n eta H.S. Black-en asmakizunen ondorioz, 1927an berrelikatutako anplifikadore elektronikoa agertu zen arte.

Routh-en lana agertu ondoren, A. M. Lyapunov matematikari errusiarra mugimenduaren egonkortasunaren arazoa aztertzen hasi zen, eta 1892an mugimenduaren ekuazio ez-linealak erabili zituen Routh-ek irizpidearen baliokidea den emaitza lortuz. Bere lana oso garrantzitsua izan zen, baina ez zen 1958 arte idatzirik agertu.

XX. mendean murgilduz gero, Lehen Mundu Gerrak, teknika guztien hobekuntzan izandako garrantziaren antzera, kontrol-sistemen erabilera ere izugarrizko eragina izan zuen eta; adibide bezala esan, berrelikatutako anplifikadoreen garapena 1945ean H. W. Bode-k idatzitako artikulu batean deskribatzen dela. Anplifikadore elektronikoek, Lehen Mundu Gerraren ondorengo lehen hamarkadetan, distantzia luzeko deiak egitea ahalbidetu zuten.

Dena den, distantzia handitzen den heinean energia elektrikoaren galera ere handituz doa burdinazko hariaren diametroa handia izan arren, eta gero eta anplifikadore gehiago jarri behar dira galerak saihestearren. Ondorioz, hainbeste anplifikadorek distortsioa ekarri zuten erabilitako huts-tutuen linealtasun-faltagatik. Arazo honen konponbidea Black-ek aurkitu zuen berrelikaduran: distortsioa ekiditeko gero eta berrelikadura handiagoa behar da. Hau da, eragingailuko bigiztako irabazpenak hazi egin behar du. Kaleko anplifikadoreen baten bolumena handitzen saiatu den edonork, Black-ek pairatutako egoera bera pairatuko luke, berrelikadurako bigiztak burrunda egin eta desegonkortu egiten baita.

4. irudia. Erreguladore zentrifugodun Watt-en lurrin-makina

1789-1800

Hemen, (teknologia berri honetan) Maxwell eta Routh-ek aipatutako egonkortasun arazoa zegoen, baina dinamika oso konplexua zenez (50. ordenako ekuazioak), Routh-en irizpideak ez zuen gauza handirik konpondu. Komunikazio-injineruak erantzun frekuentziala nahiz Cauchy-k garatutako aldagai konplexuzko matematika erabiltzen ohituta zeuden, eta, beraz, Bell laborategietako analisiak arlo konplexura bideratu ziren. 1932. urtean Nyquist-ek egonkortasunari buruzko artikulua argitaratu zuen.

Egonkortasuna, bigiztaren erantzun frekuentzialeko grafiko batzuen bidez aztertzen zen. Teoria honetan oinarrituz, berrelikatutako anplifikadoreen diseinu-metodo zabala garatu zen.

Berrelikatutako anplifikadorearekin batera, prozesu industrialetan ere berrelikatutako kontrola erabiltzen hasi zen. Arlo honetan, prozesu konplexuak, linealtasunik gabeko prozesuak eta sentsore eta eragingailuaren arteko atzerapen handiak dituzten prozesuetan, proportzional, integral eta deribatiboa den kontrola, Callender, Hartree eta Porter-ek (1936) aipatzen duten PID kontrola, erabiltzen hasi zen.

Teknologia hau, lan esperimental nahiz linealizazio-hurbilketetan oinarrituta zegoen eta PID kontroladorearen parametroen balio egokiak hautatzeko esperimentuek “sintonizazio” metodoak garatu zituzten. Garai horretan, hegazkinak gidatu eta kontrolatzeko dispositiboak azaldu ziren (garrantzi berezikoa, hegazkinen altuera eta abiadura neurtzeko sentsoreen garapena izan zen), arlo honetako kontroleko txostena 1973an Mc Ruer-ek aurkeztu zuelarik.

Bigarren Mundu Gerran izugarrizko bultzada eman zitzaion berrelikadurako kontrolari. Estatu Batuetan, MITeko laborategiko injineru nahiz matematikariek beraien jakintzak uztartu zituzten Bode-ren berrelikatutako anplifikadorea, prozesuen PID kontrola eta Wiener-en (1930) prozesu estokastikoen kontroleko teoriak garatzeko. Emaitza bezala, kontrol-mekanismo edo serbomekanismoen diseinua egiteko teknika osoaren garapena izan zen. Lan hauetariko asko, Erradiazioko Laborategian argitaratu eta jaso ziren (James, Michols eta Philips, 1947).

Kontrol-sistemen diseinua aztertzean beste ikuspegi bat ere garatu zuen 1948. urtean W.R. Evans-ek. Honek, hegazkinen gidatze- eta kontrol-sistemekin egiten zuen lan. Agertzen diren arazoetako askok egoera dinamiko desegonkorrak edo ia desegonkorrak dituzte, eta Evans-ek ekuazio karakteristikoaren azterketara bueltatzea pentsatu zuen; hau da, Maxwell eta Routh-en lanetara itzultzea.

Evans-ek, parametro bat aldatzen denean ekuazio karakteristikoaren erroen kokaera geometrikoa grafikoki jarraitzeko teknika eta erregelak garatu zituen. Bere metodoa, erroen kokapen geometrikoa, egonkortasunaren analisi eta diseinurako oso egokia da eta, gaur egun ere, teknika garrantzitsua da.

1950.eko hamarkadan, Bellman eta Kalman Estatu Batuetan, eta Pontryagin Errusian, kontrol-sistemen eredu bezala ekuazio diferentzialak erabiltzera itzuli ziren. Lan hauetako asko, satelite artifizialen kontrol-arloa garatu zen heinean agertu ziren. Gainera, 10 urte lehenago egin ezin ziren kalkuluak, konputagailu digitalekin egiten ziren. Lyapunov-en lanak, gerra-garaian Wiener eta Phillips-ek hasitako kontrol optimoaren azterketa zabaldu zuen.

Aipatutako lan horiek, Moskun 1960. urtean ospatutako Kontrol Automatikoari buruzko Nazioarteko Federazioko lehen konferentzian aurkeztu ziren. Kontrol-lan hauek ez ziren erantzun frekuentziala edo ekuazio karakteristikoan oinarritu, ekuazio diferentzialetan baizik eta, ondorioz, konputadoreen erabilera zabala ekarri zuten. Metodo horiei, kontrol modernoa deitzen zaie.

Azkenik, 70.eko hamarkadatik aurrera agertu ziren teknika berri horien artean, linealak ez diren sisteman kontrola, egokitze-kontrola, fuzzy kontrola edo aldagai anitzezko kontrola daude. Konputagailuaren agerpenarekin batera, kalkulu konplikatuak egiteko ahalmena nahiz algoritmo konplexuak erabiltzeko posibilitatea zabaldu zen. Beraz, izugarrizko aurrerapausoa eman zen kontrol modernoko tekniken garapenean, gaur egun gero eta erabiliagoak izatera iritsi arte.

Horregatik, ongi prestatutako injineru batek, teknika asko ikasi eta menperatu behar ditu, arazo baten aurrean erantzunik egokiena bilatu ahal izateko. Gainera, teknika hauetan oinarrituta, konputagailuan egindako kalkuluak erabili eta aztertzeko ere gai izan beharko du.