Karratu majikoa
1987/04/01 Goñi, Jesus Mari Iturria: Elhuyar aldizkaria
Oraingo ale honetan sorgin-karratuen gaia aztertu nahi dugu. Jakina denez sorgin-karratua izan dadin, ondorengo baldintza hauek bete behar ditu:
- zenbaki desberdinez osaturik egotea.
- zutabe, errenkada eta diagonal guztietan dauden zenbakien batura berdina izatea.
Adibidez
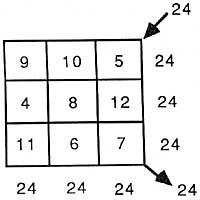
Sorgin-karratuen gai hau oso zaharra omen da eta dirudienez Matematika txinatarraren asmakizuna da. K. a. 1000 bat urte lehenago horrelako karratuak ezagunak omen ziren Ekialde Urruneko lurralde haietan.
Baina urteak pasatu dira, eta Informatikaren aroan gaudenez, ale honetan propostzen duguna zera da: maila desberdinetako sorgin-karratuak sortuko dituen programa bat prestatzea.
Egin ere, horixe egin dugu eta ondorengo lerrootan doakizue. Dena dela programa honek maila bakoitiko karratuak (3,5,7,9,11...) bakarrik sortzen ditu. Horren arrazoia oso sinplea da: maila bakoitiko karratu guztiek erregela berdinari jarraituz osatzen dira, baina erregela honek ez du balio karratuaren maila bikoitia bada. Gai honi, maila bikoitia duten karratuen gaia alegia, ondorengo artikulu baterako utziko dugu hain zuzen.
Programa azaldu baino lehen, azken oharra: sorgin-karratu baten zenbakirik txikiena edozein izatea posible denez, guk 1-10 tarteko zorizko balio bat aukeratu dugu. Hortaz, programak maila bakoitzeko 10 karratu desberdin sortuko ditu zorizko eran.
Programa honek sor dezakeen mailarik altuena 49 da, aldagaiak balio horretaraino dimentsionaturik daudelako. Maila altuagoa nahi izanez gero, dimentsio hori aldatu beharko genuke.
| 3. maila: 3 x 3 sorgin-karratua 11 6 7 4 8 12 9 10 5 errenkada, zutabe eta diagonalen batura = 24 |
| 5. maila: 5 x 5 sorgin-karratua 18 24 5 11 12 25 6 7 13 19 2 8 14 20 26 9 15 21 2 3 16 17 23 4 10 errenkada, zutabe eta diagonalen batura = 70 |
| 7. maila: 7 x 7 sorgin-karratua 31 39 47 6 14 22 23 40 48 7 15 16 24 32 49 8 9 17 25 33 41 2 10 18 26 34 42 50 11 19 27 35 43 44 3 20 28 36 37 45 4 12 29 30 38 46 5 13 21 |
| 9. maila: 9 x 9 sorgin-karratua 55 65 75 85 14 24 34 44 45 66 76 86 15 25 35 36 46 56 77 87 16 26 27 37 47 57 67 88 17 18 28 38 48 58 68 78 9 19 29 29 49 59 69 79 89 20 30 40 50 60 70 80 81 10 31 41 51 61 71 72 82 11 21 42 52 62 63 73 83 12 22 32 53 54 64 74 84 13 23 33 43 errenkada, zutabe eta diagonalen batura = 441 |
| 11 maila: 11 x 11 sorgin-karratua 73 85 97 109 121 12 24 36 48 60 61 86 98 110 122 13 25 37 49 50 62 74 99 111 123 14 26 38 39 51 63 75 87 112 125 15 27 28 40 52 64 76 88 100 125 16 17 29 41 53 65 77 89 101 113 6 18 30 42 54 66 78 90 102 114 126 19 31 43 55 67 79 91 103 115 116 7 32 44 56 80 68 92 104 105 117 8 20 45 57 69 80 93 94 106 118 9 21 33 58 70 82 83 95 107 119 10 22 34 46 71 72 84 96 108 120 11 23 35 47 59 errenkada, zutabe eta diagonalen batura = 726 |
10 CLS:KEY OFF:RANDOMIZE TIMER
12 DIM VALOR (50,50), NUM (50,50)
15 LOCATE 1,1:INPUT "karratuaren maila...",N
16 P=(N+1)/2:IF N-2*INT(N/2)= 0 THEN GOTO 15
20 FIL=1:COL=P:ALEA=INT(10*RND+1) :NUM=ALEA:VALOR(1,P)=1:NUM(1.P)=ALEA
40 FOR K=1 TO N*N-1
50 NUM=NUM=1 :COL=COL+1:FIL=FIL-1
60 IF COL N THEN COL=1
70 IF FIL 1 THEN FIL=N
80 IF VALOR (FIL,COL)=1 THEN GOTO 82 ELSE GOTO 90
82 FIL=FIL+2:COL=COL-1:IF COL N THEN COL=COL-N
83 IF COL 1 THEN COL=COL+N
84 IF FIL 1 THEN FIL=FIL+N
85 IF FIL N THEN FIL=FIL-N
90 NUM(FIL,COL)=NUM
95 VALOR(FIL,COL)=1
100 NEXT K
110 FOR K=1 TO N
112 LPRINT " ":LPRINT
115 FOR K2=1 TO N
120 LPRINT TAB(10+5*(K2-1)) NUM(K2,K1);
130 NEXT K2:NEXT K1
135 LPRINT:LPRINT
140 LPRINT " errenkada,zutabe eta diagonalen batura=";((N*N*N)+N)/2+N*(ALEA-1)
145 LPRINT:LPRINT:LPRINT
150 END
| Aurreko alean botatako mehatxu gorriak, erantzunak emango ez genituela alegia, bere lehen fruitua eman du, eta sinestea gaitza gertatzen bazaizue ere, proposatutako jolasen lehen erantzuna jaso dugula jakin behar duzue. Arrasatetik dator notizia. Jose Ramon Zubizarretak bidali digu proposatutako jolas bati dagokion erantzun bikaina. Hor duzue jasotako erantzuna. Anima zaitezte erantzun gehiago bidaltzera. "Agur t'erdi: Abenduko aldizkarian proposatutako jolas matematikoari erantzuna: Zenbakia A, B, C zifraz osaturikoa dela pentsa dezakegu. 6 zifrako zenbakia: ABCABC. Zenbaki hau beste era honetan idatz daiteke: A x 10 5 + B x 10 4 + C x 10 3 + A x 10 2 + B x 10 + C (m.m.) Agur bero bat eta beste bat arte." |
