Chaos in the Solar System

1992/10/01 Arregi Bengoa, Jesus Iturria: Elhuyar aldizkaria

• Astronomia

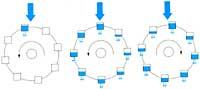
In the last three decades scientists are making great efforts to approach the explanation of the behavior of non-linear dynamic systems. Unlike what is believed, these systems do not always evolve into states of equilibrium or periodic behavior. For the first time E. Lorenz demonstrated in 1963 that non-linear dynamic systems often evolve in a totally chaotic way. The system of three nonlinear differential equations and three unknowns that he studied describes the behavior of the trens called water wheel or Lorenz wheel. It is a good example to understand the type of system and the behavior we refer to. Figure 1 shows the outline. Water falls evenly down the top source. The containers are perforated and they also lose water evenly.

If the tap flow is small, the top container will not be filled and friction will prevent movement. If the flow is large enough, the wheel will start spinning. The instrument can achieve a constant turning speed and stay in that movement. If the source flow is greater, the turn will be faster and the non-linearity of the system will become more important. Then, the containers will have less time to fill and, on the other hand, they will empty very little before going up. As a result, the containers that go up can be heavier than those that go down and the turn will be reversed.

According to Lorenz, if the device is abandoned by itself, the turn can vary in many ways, never at a constant speed or any other instruction that makes it a predictable system. This behavior is also found in the Solar System. After having evolved cyclically for thousands or millions of years the peculiarities of the object's orbit, their behavior changes sharply. It is useless to know the movement until then, since from that moment on evolution cannot be foreseen. Before giving examples, we must mention another feature.

Scientists, regardless of the field in which they worked, have always accepted that small changes in initial conditions, as well as small disturbances that may occur throughout the process, produce minimal changes in results. The same is not true in chaotic systems. That is the problem that led to E. Analyze the Lorenz non-linear dynamic system. His initial intention was to adequately describe the atmosphere for meteorological predictions. To do this, we tried to write the appropriate equations to join the variables temperature, pressure and wind speed. He finally started working with a system of twelve equations. Of course, it was a non-linear system. Therefore, undeliverable analytically. That is why he used the help of a primitive computer of the time, using numerical methods.

When entering the initial data, he realized that a very small difference he considered irrelevant provoked in a few days a totally different time: this phenomenon is called sensitive dependence on the initial conditions. It is often also known as a butterfly effect. Time, then, cannot be fully foreseen in the long run. The disturbance caused by the flight of a butterfly can also be enough to change the time of a region in a few days.

It may be thought that studying the movement of the components of the Solar System is easier than studying the evolution of the atmosphere. It seems that the complexity of the atmosphere cannot be compared to that of the Solar System, although asteroids are also taken into account. However, the theoretical problems posed by the study of the Solar System are also very important. Although in mechanics one can easily liberate what is called the problem of two bodies, the system of equations describing the movement of the system formed by three bodies cannot be released analytically. H. This result demonstrated by Poincare makes it impossible to predict the long-term evolution of the system. To overcome this difficulty, astronomers often calculate their orbits using percussion theories. They retain the appropriate themes to the equations to take into account the influence of all bodies.

In the mid-1950s, a theorem on dynamic systems similar to the Solar System was a theoretical advance. Applied to the Solar System it predicts its stability when the masses of the planets and the eccentricity and inclination of their orbits are small over time.

With these theoretical bases and the inevitable help of the first high-powered computers, a first significant study on the stability of the Solar System began to be carried out. For example, in 1965 the stability of the five outer planets was predicted for the next 120,000 years. Later the deadline was extended to a million years, but it was also discovered that Pluto has resonances with Nepturo. Although it did not give them importance then, these periodic gravitational interactions are now considered to be the first trace of the chaos of the Solar System. In another study published in 1985, the stability margin extended to 5 million years.

As in the previous case, Pluto's resonances appeared, but the period analyzed until then was too short for chaotic behavior to appear. The following year J. Wydow and G. Sussman worked on the orbits of the same planets, first studying their appearance and appearance in the previous 107 million years and in the future 110 million years, and then extending the second term to 845 million years. The period of calculation of the particularities of the orbits was 32.7 days. Some interesting results are those mentioned immediately. The inclination of Pluto's orbit varies between 14.6º and 16.9º (now it is 17.2º). The resonances that Neptune causes Pluto cause this last planet to suffer oscillations of 3.8, 34, 150 and 600 million years. Finally, a slight change in the initial conditions of Pluto's orbit causes the new orbit to move exponentially away from the initially calculated one. The last two results are, above all, indicators of chaos.

More recently the LONGSTOP study (Longterm Gravitational Stability Test for Outer Planets) also explains in its conclusions the phenomena that can be indicators of Chaos. For example, although the variations that orbits suffer are small, they are of the membranous period.

It is also a study on the inner planets, J in 1989. Presented by Laskar. Using the equations of motion in a simplified analytical way, this scientist has calculated the orbits of the inner planets in steps of 500 years for the next 200 million years. Like the outer planets, the interiors also experience small variations in their orbits, but the sensitive dependence on the initial conditions is evident. Resonances also appear. However, these tracks of chaos should not make us think that planets have to be seen crossing orbits and causing disasters. The problem is posed differently: although the orbits of the planets have not changed too much, in no case can we predict the position of the planet in the long term.

So far we have spoken of the stability of the orbit of the planets, or what is the same, of the influence of chaos on those orbits. For the whole structure, we could raise other questions, what will be the influence of chaos on the configuration of the Solar System? Did their current appearance and relative stability achieve them in the first thousands of years of their constitution, or have they achieved it over their nearly 5 billion years?

There are those who believe that it is possible that at one time there are other planets that then fell into chaotic behavior and would be expelled, but, of course, it is impossible to prove it. Others believe that the influence of chaos has been limited, affecting only the dynamics of asteroids and other small bodies. The most concrete and tangible cases of chaos on this level will be seen in the following issue.

October Ephemeris SUN : 23 October enters Scorpius at 3h 57min (UT). LUNA Growing room Full moon Recent searches New moon day time (UT) Services 14h 12min Results 18h 3min Information 4h 12min Services 20h 34min PLANETS: MERCURY: will reach its maximum elongation on October 31. If we see it, we will see it that day or those around us, but it will not be easy, because it will be kept behind the Sun before the hour. VENUS: Venus will also be very shortly after sunset above the horizon. Therefore, it is not a good time to see it. However, it is hidden shortly after Mercury. MARTITZ: Martitz comes out every time before. In mid-October will leave at 21 h (UT). JUPITER: after not being able to see it in September, we will begin to see it in the morning in October. It leaves every day before and we can see more time, but still low, in the sky. SATURN: we can still see it well as it darkens, it will hide at the beginning of October at midnight, but in the end it will go to us at 23h (UT).