Teorías de Kaluza y Klein: un mundo de once dimensiones

1987/04/01 Martinez Lizarduikoa, Alfontso Iturria: Elhuyar aldizkaria

• Fisika

1.- Modelo y gravitación de Kaluza

A distancia, el cable parece una línea curva. Más cerca, sin embargo, vemos que el punto P es un círculo. Es posible que en el espacio de la tridimensión lo que normalmente consideramos como punto sea un pequeño círculo alrededor de otra dimensión espacial. Esta es la idea básica de Kaluza y Klein en la teoría unificadora de las fuerzas electromagnéticas y gravitatorias.

El antiguo sueño de Einstein (unir el campo gravitatorio y electromagnético con la descripción geométrica) fue reinventado por el físico polaco Theordor Kaluza y hacia 1921 trató de expresar por geometría la teoría electromagnética de Maxwell. Pero para llevar a cabo este proyecto era necesario remodelar la propia geometría para que la Electromagnética se moldiera dentro de esa geometría.

Para lograrlo, Kaluza postuló una dimensión espacial adicional, con lo que la geometría que depende de la naturaleza tendría cuatro dimensiones espaciales y un tiempo. La gravitación en este mundo de cinco dimensiones sería el resultado de la suma de la gravedad normal y del campo electromagnético de Maxwell. Si fuéramos capaces de ampliar nuestra percepción en cinco dimensiones, nos encontraríamos con un único campo de fuerza: el gravitatorio. Según esta teoría, la onda electromagnética sería la ondulación de la dimensión quinta.

La teoría de Kaluza obtuvo un gran éxito matemático. Pero también tenía una cola insuperable. Es decir, si el universo espacial es de cuatro dimensiones, ¿por qué no se puede captar físicamente la cuarta dimensión? ¿Esa cuarta dimensión será sólo una maña matemática?

2.- Estructura pentadimensional de Klein

En 1926 el físico sueco Oscar Klein trató de demostrar la compatibilidad de la estructura pentadimensional y mecánica cuántica de Kaluza. Para ello, proporcionó una nueva versión de la ecuación de Schrödinger adaptada a las cinco dimensiones. Para Klein, la cuarta dimensión espacial tiene una existencia real.

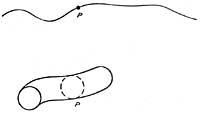
Para entender mejor esto, supongamos una línea y un círculo asociado a cada punto de esa línea. La unión de la línea de una dimensión con el círculo de una dimensión crea un cilindro de dos dimensiones. Supongamos también un plano en el que todos los puntos de ese plano están adaptados a un círculo, entonces la unión entre el plano bidimensional y el círculo de una dimensión creará uno en tres dimensiones continuas.

Con el mismo razonamiento se puede adivinar que en cada punto se le añade un continuo tridimensional y un círculo, que están rizados en la cuarta dimensión. Estos bucles no se rizarían en el espacio, porque no están dentro del espacio. Lo que hacen estos espirales es expandir el espacio.

Klein comenzó el cálculo de las circunferencias de estos círculos que crean un universo de cinco dimensiones. Para ello tuvo en cuenta las cargas de electrones y otras partículas, como las fuerzas gravitatorias entre ellas. En caso de realizar los cálculos, indicó que la longitud de estos círculos sería de entre 10 y 30 cm.

Su pequeña cifra nos indica por qué la quinta dimensión no puede ser percibida correctamente. Esta cifra es tan pequeña que, además de un ser vivo, ningún átomo podría moverse por estas dimensiones.

Esta dimensión está situada dentro del átomo. Para detectar una estructura tan sutil, deberíamos disponer de un acelerador de fracciones de varios años de luz.

3.- Generalización de modelos de Kaluza-Klein: un mundo de once dimensiones

El modelo de Kaluza/Klein fue olvidado durante varios años. Sin embargo, en los últimos años ha surgido la pasión de este modelo entre los científicos, pero ahora en un contexto diferente: Es decir, en el contexto de las Teorías de Mayor Unión y las Teorías Supergravitatorias.

Con el objetivo de unir las fuerzas de la naturaleza, en una teoría se han propuesto siete dimensiones desconocidas del Universo. Se puede expresar como una estructura compacta pequeña, como si cada punto de la esfera tuviera en cada momento una esfera adherida. Las esferas situadas en las intersecciones de las líneas de coordenadas son dimensiones adicionales agrupadas postuladas en la nueva teoría. Las esferas son tangentes en cada punto respecto al plano. Además, la esfera y el plano generan sólo cuatro dimensiones y no 11 de la teoría. Las cuatro dimensiones son las cuatro coordenadas que definen un punto.

La teoría de Kaluza/Klein se ha reintegrado en el campo de la Física, suponiendo que la simetría de los campos de fuerza es el resultado de una estructura geométrica interna en la Naturaleza. Es más, las simetrías gauge son formas de geometría añadidas a las nuevas dimensiones espaciales.

Los problemas que debería cubrir la teoría generalizada de Kaluza/Klein son los tres siguientes. Primero tendrá que rellenar un campo fermónico para indicar los fermiones que hay en nuestro universo. También debería indicar al menos un campo bosónico y, por supuesto, el campo gravitatorio (origen de las dimensiones espirales ocultas). El modelo que cumple todos estos requisitos es una versión de la supergravedad 11. Por tanto, la moderna teoría de Kaluza/Klein postula un universo de 11 dimensiones. Siete de estas once dimensiones estarían enrolladas hasta un nivel en el que quedarían ocultas para la observación directa.

A las dimensiones en las que aparecen enrollados le corresponden un gran número de tipos de topologías, por lo que hay que llevar a cabo un proceso concreto para elegir la más adecuada:

Resolver ecuaciones de supergravedad. Algunas de estas medidas podrían corresponder a cuatro dimensiones espacio-temporales y a una forma topológica cerrada de siete dimensiones. A continuación, estudiaríamos el conjunto de simetrías de cada superficie correspondiente a la resolución de ecuaciones. El conjunto de simetrías nos define la teoría no abelina gauge que debe unirse a la gravedad. Las diferentes superficies cerradas presentan distintos tipos de simetrías, y cada una de ellas define una Teoría diferente de las Grandes Uniones.
1. Finalmente, se analizan las estructuras de ondas estacionarias permitidas por superficies cerradas. Estas estructuras definirán las características de las fracciones que predice la teoría en un espacio-tiempo normal de cuatro dimensiones.

4.- Heptaesfera

En todas las topologías que se pueden conseguir, los matemáticos han elegido una topología especial por sus características: Heptaesfera (equivalente en siete dimensiones de la esfera). Mediante este modelo se describen todas las estructuras que van desde el átomo más pequeño hasta la galaxia más grande.

Si esta esfera de siete dimensiones se deforma, puede aparecer el ocultamiento de las simetrías y la ruptura brusca. Por estas razones este modelo ha sido considerado óptimo.

¿Sería posible sondear y detectar físicamente esta esfera?. Según cálculos recientes, la longitud de la circunferencia de esta heptaesfera es de entre 10 y 32 cm. Esta dimensión se sitúa junto a la menor distancia con sentido físico utilizada en Física, la distancia de Planck.

La diferencia del principio de incertidumbre de Heisenberg para sondear la heptaesfera de Kaluza/ /Klein sería 1019 veces mayor que la masa del protón. En este nivel energético podemos ver una estructura espacial temporal de once dimensiones. Pero para conseguirlo necesitaríamos un acelerador de fracciones tan grande como la Vía Láctea de Ortz.

Sin embargo, en las investigaciones llevadas a cabo en los últimos años han surgido importantes problemas que en muchas ocasiones no son conciliadores con el mundo de cuatro dimensiones que nosotros conocemos y estudiamos. Uno de estos problemas es: En todos los mundos de once dimensiones analizados se predice la existencia de neutrinos dextrógiro y levógiro. Esto no se corresponde con la experiencia que tenemos. En nuestro mundo todos los neutrinos son levógiros.

Una partícula pequeña con forma de cordón o cuerda tiene una sola dimensión. En la teoría de las supercuerdas, las cuerdas son extremadamente pequeñas y se mueven en un espacio y tiempo similar de 10 dimensiones. Las propiedades de la teoría de las supercuerdas para las páginas del universo se están investigando en la actualidad y están estrechamente relacionadas con algunos problemas importantes de la matemática contemporal.

Hay otro problema. Las dimensiones enrolladas en los mundos de Kaluza/Klein dan una gran curvatura a otras dimensiones espacio-temporales. Esto crea una gran contradicción con las observaciones astronómicas actuales, ya que según estas últimas la curvatura media del universo es prácticamente nula.

5.- Perspectivas actuales

Los problemas mencionados y los infinitos de la gravitación cuántica han estado presentes en los últimos años. En la actualidad (según los avances realizados a lo largo de 1985) se habla de un universo de diez dimensiones entre científicos y la llamada teoría de las Supercuerdas (1) para explicar este universo ha generado grandes expectativas.

Llegados a este punto, recordaremos que el desarrollo de las teorías gaudí no abelianas que se utilizan tardó unos diez años en desarrollarse. Por eso, para reforzar las relaciones entre la supergravedad y las teorías de Kaluza/Klein, es posible que pasen varios años. Mientras tanto, habrá que desarrollar trabajos teóricos y matemáticas especiales que impliquen estas teorías.

El binomio Matemática/Física tiene cada vez más importancia. El descubrimiento matemático que impulsó la teoría física de la supergravedad fue el número más anticonmutante. La matemática que necesita la teoría física de la gravitación cuántica está aún por crear.

OBSERVACIONES

En esta nueva teoría, las fracciones básicas (quantos) se sustituyen por unas cuerdas en vibración. A cada vibración le corresponde una fracción. En esta superteoria se combinan la teoría de las cuerdas y la supersimetría.