Grabitazio kuantikoa. Teoria supergrabitatorioak

Sarrera

Elektrodinamika kuantikoak lortutako arrakastak zientzilariak eremu elektromagnetikoa eta ahula batzera bultzatzen ditu, eta horretarako gauge simetria boteretsuagoa asmatu behar da. Simetria berri hori spin-eko simetria isotopikoan eta simetriaren bapateko etenduran oinarritzen da. Teoria elektroahul hau, 1983an esperimentalki baieztatu zen.

Ildo horri jarraituz, gauge eremu ahaltsuagoa teorizatzen saiatzen ari dira indar bortitza batzeko asmoz. BHT (1) teoriak sortu dira. Teoria hauek egun oraindik ez dira esperimentalki baieztatuak izan. Baina fisika teorikoak ez dauka itxaroterik eta beste eremu zabalagoa teorizatzen hasi da aurreko indarrekin grabitatorioa batzearren. Teoria superzabal hori lortzea da grabitazio kuantikoaren helburua.

1.- Bosoien eta fermioien unibertsoa

Batasunik Handieneko Teoriek (BHT), mundu fisikoaren hiru eremu batzen dituzte, baina laugarrena ez; grabitazioarena alegia. Grabitateak erresistentzia izugarria du beste indarrekin batzeko.

Testuinguru honetan bi arazo sortzen dira. Alde batetik ez dugu ezagutzen lau indarrak batzeko behar den simetriarik. Bestetik ez daukagu oraindik mekanika kuantikoarekiko konpatible izan daitekeen teoria grabitatoriorik, zeren eta grabitazioa grabitoien (eremu grabitatorioko kuantoak) elkartrukaketaren bidez definitu nahi denean, infinituak agertzen dira teoria deuseztatuz.

Baina badakigu zer egin litekeen infinitu horiek desager daitezen: Orain arte edozein teoriak duena baino simetria potenteagoa sorterazi. Eta hori izan zen hain zuzen ere fisika teorikoak aukeratu zuen bidea. 1970. urtean fisikariek lehenengo teoria supergrabitatorioak aldarrikatu zituzten. Teoria hauetan erabilitako simetria hain potentea da, ze naturan existitzen diren indar guztiak batzen bait ditu. Horregatik teoria hauei supersimetriko esaten zaie.

Supergrabitazioa, Einstein-en erlatibitatearen teoriaren jeneralizaio bat da. Supergrabitazioak fenomeno grabitatorioak maila kuantikoan deskribatzen ditu.

Supergrabitazioa, grabitazioaren formulazio supersimetrikoa da. Supersimetria hau, 70. urtealdiaren hasieran formulatua izan zen independente ziren hiru bideetatik. Ikerketa horiek Estatu Batuetan, Sobiet Batasunean eta Europan gauzatu ziren.

Ikerketa horien mamia hauxe da. Unibertsoan dauden zatiki guztiak bi taldetan bana daitezke beren spin-ari dagokionez: Bosoiak eta fermioiak dira bi taldeak. Bosoiak spinik eza edo spin soila duten partikulak dira. Fermioiak, ez: hauek spin-en frakzioak dituzte. Horrek, gure adimenarako oso gogorra bada ere, partikula horiek errotazio bikoitza dutela esan nahi du.

Era honetan banatutako zatikien jokabidea oso bitxia da. Fermoiek ez dute harremanik izan nahi beren familiako beste partikulekin. Jokabide hori Pauli-ren esklusio-printzipioaren bidez definitua gelditzen da. Printzipio horren arabera, bi fermioik ezin dute zenbaki kuantiko berdina elkarren artean banatu.

Hain berekoia den jokabide honen aurrean, bosoiak ditugu. Hauek beren artean lan egiteko ez dute oztoporik jartzen eta taldetan biltzen dira maila bateraino, beren efektuak biderkatuz, non gure neurketa-lanabesen bitartez makroskopikoki detektatuak izan bait daitezke.

Jokabide hori dela eta, fermioien eta bosoien munduak beti batabestearen gisa hartu izan dira mundu zientifikoan. Horregatik, harriduraz hartuak izan ziren teoria supergrabitatorio hauek, zeren eta beraien oinarriak bosoi eta fermioien batasunean bait zeutzan.

2.- Supersimetria

Teoria supersimetrikoa, ezaugarri konmutatiboa ez duten zenbaki-elementuetan oinarritzen da. Zenbaki horiek sartzearen arrazoia, Pauli-ren esklusio-printzipioarekin erlazionatuta dago. Printzipio honek puntu batetan bi fermioi batera egotea debekatzen du.

Supergrabitatearen jatorria, supersimetriak duen ezaguarri harrigarri batean oinarritzen da. Fermioi-bosoi transfomakuntza behin eta berriz aplikatzen bada alegia, partikula bat espaziodenboran zehar puntu batetik bestera higitzen da. Partikula honen desplazlamendua transformakuntza supersimetriko baten bitartez lortzen bada, horrek supersimetriaren eta espaziodenborazko egituraren artean harreman sakona existitzen dela aditzera ematen du.

Gainera supersimetriaren transformazioaren errepikapena Poincaré-ren transformakuntza baldin bada eta Poincaré-ren inbariantza murriztuak erlatibitate orokorra sorterazten duen simetria dela kontutan hartzen bada, hortik supersimetriaren eta grabitazioaren artean oso konexio estua existitzen dela ondorioztatuko da. Horregatik hasi dira hain zuzen fisikari teorizaleak teoria supersimetrikoak aztertzen.

2. irudia. 10 ^-15 zentimetroko eskalaraino, elektrodinamika kuantikoaren teoriak balio duen eskalan alegia, espaziodenbora erabat "leun" eta jarraia agertzen da (A). 10 ^-30 eskalan ordea, imajina horrek ez du balio. Mailatu eta zimur batzuk agertuko lirateke (BN). Planck-en luzerako eskalan (10 ^-33 cm), J. Wheeler-en arabera espaziodenborak bere topologia betirako aldatzen duen topologia eskaintzen du (C).

Gauge teoria supersimetrikoaren oinarria da lehen esan dugunez, bi errotazio supersimetrikoek espaziodenboran sorterazten duten desplazamendua. Fisikoki honako erara interpreta daiteke: Supersimetria baten transformakuntzaren errepikapenak zatiki fisiko bat desplazarazten du.

Teoria supersimetriko murriztua lortzeko, simetria (errotazio) bakoitzari gauge eremu bat erantsi behar diogu. Bitartean espaziodenboran sortutako desplazamendua Poincaré-ren transformazioa da. Transformazio hori dela eta, grabitoia gauge partikula egokitzat har liteke. Horrela, besterik gabe teoria supersimetrikoa teoria supergrabitatorio bihurtzen da.

Supergrabitateak bada, erlatibitate orokorraz deskribapen bat ematen digu, bere hizkuntza kuantikoa delarik. Teoria honek 3/2 spin-eko partikulen existentzia aurresaten du. Partikula horien behaketa esperimentalak supergrabitazioari bultzada handia emango lioke.

3.- Supergrabitazioaren teoria orokorrak

Lehen aipatutako supergrabitatea, teoria batuzko multzoan orokortu izan da, multzo horri Supergrabitazioaren teoria orokor esaten zaiolarik.

Multzo horretan 8 teoria ditugu. Horien artean N=1 da (2), grabitazioa bere jatorriko eran. Eta potenteena N=8 da. Eredu honetan oso ugaria den zatiki-familia definitzen da. Familia horretan 70 partikula ditugu. Partikula horien artean gaur egun ezagutzen diren guztiak eta aurkitu behar diren beste hainbeste koka daitezke. Horrelako eredu batek fisikaren eremu guztiak batzen ditu. Beste erara esanda, teoria hori, Natura osoa kontrolatzen duen ente bakar bat izango litzateke. Marko horretan, lehenengo aldiz zientziaren historian, materia eta indarra deskribapen bakar batez azalduko lirateke.

Teori multzo honen lorpenik handiena, haietan lortzen den simetri maila da. Supersimetria, barneko simetriarekin elkartzen denean, grabitoiak sorterazten dituen zatiki guztiak baturik gelditzen dira. Eta hori oso garrantzitsua da, zeren eta diagrama guztiak grabitatorioaren diagramaren funtzioan defini bait daitezke. Eta diagrama guzti horien batura (elkarrekintzen probabilitatea kalkulatzeko) finitua da. Beraz, teoria hauek birnormalizakorrak dira.

Birnormalizazioa, simetria sakona, eremuen batasuna,... horiek dira teoria supergrabitatorioek lortu dituzten helburuak. Fisikariek (fisikari teorizaleek) izugarrizko konfidantza dute teoria horietan. Batzuek, N=8 teoria fisika teorikoaren gailurra dela esaten dute.

Gaur egun arte teoria fisikoak, errealitatea interpretatzeko eredu bezala izan dira hartuak. Eredu horiek hobetu ahala, teoriaren eta erralitatearen arteko elkarsartzea egokitzen zen. Gaur egungo zientzilari batzuk honako eritzia azaltzera ausartu dira:

"N=8 teoria supergrabitatorioak errealitatearekin egokitasun matematiko ikaragarria du, zeren teoria hori ez bait da jadanik errealitatearen eredua; errealitatea baizik".

4.- Espaziodenborazko jarraikiaren kuantizazioa

Grabitazio kuantikoak duen alderik izugarriena eta ilunena, espaziodenborazko markoaren gain kuantizazioak izan dezakeen eragina da.

Lehen aipatua izan denez, teoria batua lortzeko grabitazioak eta mekanika kuantikoak konpatible izan behar dute. Beste erara esanda, eremu grabitatorioa kuantizatu egin behar da. Baina erlatibitatearen teoria orokorrak dioenez, eremu grabitatorioa ez da espaziodenborazko jarraikiaren deformazio bat baino.

Puntu honetan korapilo garrantzitsu bat sortzen da, zeren eta grabitatea kuantizatzen bada, gertakari fisikoen markoa bera ere (espaziodenborazko jarraikia) objektu kuantiko bihurtuko bait da. Eta azkeneko honek izugarrizko inplikazio fisiko-filosofikoak izango ditu.

Eremuen teoria kuantiko arruntean, espaziodenborazko substratoa egonkorra zen. Grabitazio kuantikoaren teorian berriz, euskarri (substrato) hori ez da bere barnean gertatzen diren fluktuazio kuantikoez bakarrik eragina izango; bera ere fluktuakorra izango da.

Ikuspuntu honetatik mikrokosmo-mailan espaziodenborazko markoaren jokabidea aztertzen badugu, hiru maila desberdin agertuko zaizkigu.

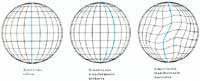
Lehenengo mailan, 10 ^-12 cm-ko maila espazialean gutxi gorabehera (Planck-en luzera baino askoz maila altuagoa da), atomoaren nukleoa aurkitzen dugu. Maila honetan, eremu grabitatorioaren fluktuazio kuantikoak oso txikiak dira, eta substratoaren geometria jarraitzat har daiteke.

Distantzien maila jaisten bada eta 10 ^-30 cm-ra heltzen bagara (Planck-en inguruko uhin-luzera), BHT eskalara murgiltzen gara (3). Maila honetan, substratoaren geometrian fluktuazio garrantzitsuak agertzen hasten dira eta lehen topologia launa zena orain zimurtua azaltzen da.

Distantzien eskalan jaisten jarraitzen badugu, Planck-en luzeraraino helduko gara (10 ^-30 cm); esangura fisikoa duen distantziarik txikienera. Hemen espaziodenborazko jarraikiak indartsu fluktuatzen du, ekaizpean itsasoko olatuen artean aurkituko bagina bezala. Espaziodenbora hau kuantizatua dago eta bere egitura kausala fluktuakorra eta definitu gabekoa da.

3. irudia. Einstein eta Rosen-ek 1935.ean pentsatutako bi gainazalen espazioan, eremu elektrikoaren indar-lerroak beheko gainazalean elkartu egiten dira eta goikoan banatu (A). Espazio honen geometriak, beheko gainazalean karga elektriko negatibo efektiboa agerterazten du, eta positiboa goikoan. Horren antzera, fluktuazio topologikoa bi karga efektibo (positiboa eta negatiboa) sortzeko iturria izan daiteke (B). Wheeler-en ereduak iradokitzen duenez, fluktuazio topologikoak izan daitezke "oinarrizko partikulen" kausa.

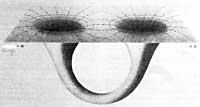
Planck-en eremuaren eskalan ez dago iraganaldia eta geroaldia bereizterik. Hain izugarri txikiak diren distantzia hauetan, seguraski erlatibitate ez-kuantikoan permititzen ez diren prozesuak gerta daitezke; argiaren abiadura baino handiagoak diren beste abiaduren existentzia adibidez.

5.- Topologia aldakorra

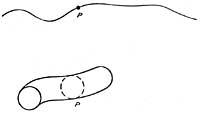
Testuinguru honetan Wheeler-ek asmatutako topologia aldakorraren kontzeptua sortzen da. Kontzepzio horren arabera eremu ahulak Planck-en eremuetara estrapolatzen badira, geometriaren fluktuazioak oso oldartsuak izan litezke espaziodenbora berean zulo beltzak sorteraziz. Horrelako egoeran, substratoaren topologia errotik aldatua agertuko litzaiguke. Marko horretan, biolentzia eta desoreka errege izango lirateke. Euskarriaren egitura espaziodenboralak oso konplexuak izanik, sortuz eta desagertuz arituko lirateke.

Wheeler-en teoriaren arabera, hain oldartsu den itsaso espaziodenboral horren esitenziak, oinarrizko partikulen bidez bere burua ezagutzera emango luke. Eta partikulen arteko izaera desberdina, kitzikapen bakoitzari erantsitako topologiak zertzen du. Wheeler-ek dioenez, oinarizko zatikien jokabideak ezagutzeko grabitazio kuantikoaren egoeraren izaera ulertu beharko genuke lehenago. Oinarrizko partikulan fenomenologia beraz, geometriaren kimikara laburturik geldituko litzateke.

Zein ote da kaos kuantiko hau deskribatzeko erabil datiekeen eredu matematikoa?. Nola deskribatu marko horretan gertatzen diren trantsizio topologikoak?

Eredu batzuk jadanik proposatu dira (4), baina giro zientifikotan adostasun osorik ez da lortu. Zientzilari batzuek, geometria espaziodenborala bigarren mailako errealitate bezala kontsideratzea proposatu dute. Errealitate horrek Planck-en distantzietan bakarrik izango luke garrantzia. Baina azalpen honek beste arazo bat dakar: Zein ote da errealitatearen izaera berria, grabitazio kuantikoan substrato espaziodenborala ordezkatu behar bada?

Galdera horri emandako erantzuna, bi alde desberdinetatik konformatzen ari da. Lehenengo aldea, orain arte aipatu dugun teoria supergrabitatorioa da, dagozkion bere simetria ahaltsuekin. Bestetik, orain dela hirurogei urte Kaluza-k eta Klein-ek sortu zituzten dimentsio anitzeko munduak berraztertzea da, baina perspektiba kuantikoaren ikuspegitik orain berrinterpretatuak. Dimentsio askotako unibertso horiek izango dira hurrengo kapituluan aztertuko ditugunak.

BHT: Batsunik Handieneko Teoriak
GUT: Grand Unified Theories
GTU: Grandes teorias Unificadas
N da, teoria bakoitzaren 3/2 spin-a duten grabitinoen kopurua.
Eskala honetan quark eta leptoiek identitatea galtzen dute, eta indar elektromagnetikoa, ahula eta bortitza, batzen dira.
Berriki, S.W. Hawking-ek eredu matematiko bat aurkeztu du espaziodenborazko topologia deskribatzeko. 1984 urtean topologia horren transformaziorako kalkulu hurbila aurkeztu da. Puntu hau zehatzago aztertzeko ikus A. Strominger bibliografian.

• DAVIES, Paul: The edge of Infinity ; J.M. Dent and Sons Ltd., London, 1985.
• DE WIT Bryce: Gravedad cuántica ; Scientific American, Ots, 1984.
• DUFF M.J. ISHAM C.J.: Quantum Structure of Space and Time ; University Press, Cambridge, 1982.
• STROMINGER, A.: Phys. Rev. Lett. , 52, 1733; (1984).
• WEINBER, S: Teorias unificadas de las interacciones entre partículas elementales ; Scientific American, Uztaila, 1974.