Kaluza eta Klein-en teoriak: hamaika dimentsioko mundua

1.- Kaluza-ren eredua eta grabitazioa

Urrutitik begiratuta, kableak lerro kurbatua dirudi. Hurbilagotik begiratuta ordea, P puntua zirkulua dela ikusten dugu. Baliteke guk hirudimentsioko espazioan normalean puntu bezala hartzen duguna espazioko beste dimentsio baten inguruko zirkulu txiki bat izatea. Hau da Kaluza eta Klein-ek indar elektromagnetiko eta grabitatorioen teoria bateratzailean duten oinarrizko ideia.

Einstein-en aspaldiko ametsa (eremu grabitatorio eta elektromagnetikoa deskribapen geometrikoaren bidez batzea) Theordor Kaluza fisikari poloniarrak bere eskuetan berrartu zuen eta 1921. urte inguruan Maxwell-en teoria elektromagnetikoa geometriaren bidez adierazten saiatu zen. Baina horrelako proiektua aurrera eramateko, geometria bera birmoldatu behar zen, Elektromagnetika geometria horren barnean molda zedin.

Hori lortzeko Kaluza-k, espaziorako dimentsio gehigarri bat postulatu zuen, era horretan naturaren baitan dagoen jarraiki geometrikoak lau dimentsio espazial eta denbora bat izango zituelarik. Bost dimentsioko mundu honetan grabitatzioa, grabitate arruntaren eta Maxwell-en eremu elektromagnetikoaren batuketaren emaitza izango litzateke. Gure pertzepzioa bost dimentsiora zabaltzeko gai izango bagina, indar-eremu bakar bat atzemango genuke: grabitatorioa. Teoria honen arabera, uhin elektromagnetikoa bostgarren dimentsioaren uhindura baino ez litzateke izango.

Kaluza-ren teoriak arrakasta matematiko handia lortu zuen. Baina bazeukan gainditu ezinezko koxka ederra ere. Alegia, unibertso espaziala lau dimentsiokoa baldin bada, zergatik ez dago laugarren dimentsioa fisikoki atzematerik? Laugarren dimentsio hori maina matematiko bat besterik ez ote da izango?

2.- Klein-en egitura pentadimentsionala

1926. urtean Oscar Klein fisikari suediarra Kaluza-ren egitura pentadimentsionalaren eta mekanika kuantikoaren konpatibilitatea frogatzen saiatu zen. Horretarako Schrödinger-en ekuazioaren bertsio berri bat eman zuen bost dimentsioei egokituta. Klein-entzat laugarren dimentsio espazialak existentzia erreala dauka.

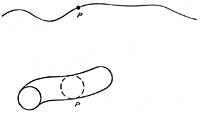
Hau hobeto ulertzeko demagun lerro bat, eta lerro horren puntu bakoitzari elkartua dagoen zirkulu bat suposa dezagun. Dimentsio bateko lerroaren eta dimentsio bateko zirkuluaren elkarkidetzak bi dimentsioko zilindroa sorterazten du. Era berean demagun plano bat, plano horren puntu guztiak zirkulu bati egokituta daudelarik; orduan, bi dimentsioko planoaren eta dimentsio bateko zirkuluaren elkarkidetzak hiru dimentsioko jarraiki bat sorteraziko du.

Arrazonamendu berberarekin asma liteke hiru dimentsioko jarraiki bat eta puntu bakoitzean zirkulu bat eransten zaiola, zirkulu txiki horiek laugarren dimentsioan kizkurtuak daudelarik. Kiribil hauek ez lirateke espazioan bertan kizkurtuko; espazioaren barnean ez bait daude. Kiribil hauek egiten dutena espazioa bera hedatzea da.

Klein-ek, bost dimentsioko unibertsoa sorterazten duten zirkulu horien zirkunferentzien kalkuluari ekin zion. Horretarako elektroi eta beste partikulen kargak, hala nola haien arteko indar grabitatorioak, ere kontutan hartu zituen. Kalkuluak eginez gero, zirkulu horien luzera 10 ^-30 cm koa izango litzatekeela aditzera eman zuen.

Horren zifra txikiak, bostgarren dimentsioa zergatik atzematerik ez dagoen zuzen adierazten digu. Zifra hori hain txikia denez, izaki bizidun bat ezezik atomo bera ere ezin izango litzateke horrelako dimentsiotan zehar mugitu.

Horrelako dimentsioa, atomoaren barnean kokatua dago. Hain sotila den egitura detektatzeko, zenbait argi-urteko luzera lukeen zatiki-azeleragailua eduki beharko genuke.

3.- Kaluza-Klein-en ereduen jeneralizazioa: hamaika dimentsioko mundua

Kaluza/Klein-en eredua urte batzuetan zehar ahaztua izan zen. Hala ere azkeneko urteetan eredu honen grina sortu da zientifikoen artean, baina orain testuinguru desberdinean: Batasun Handieneko Teorien eta Teoria Supergrabitatorioen testuinguruan alegia.

Naturako indarrak batzeko asmoz, Unibertsoaren zazpi dimentsio ezezagun proposatu dira teoria batean. Egitura trinko txiki bezala adieraz daiteke; esferako puntu bakoitzak une bakoitzean esfera bat itsatsia balu bezala. Koordenatu-lerroen elkargunetan dauden esferak, teoria berrian postulatutako dimentsio gehigarri bilduak dira. Esferak, planoarekiko puntu bakoitzean ukitzaile dira. Gainera esfera eta planoak lau dimentsio bakarrik sortzen dituzte, eta ez teoriako 11. Lau dimentsioak, puntu bat zehazten duten lau koordenatuak dira.

Kaluza/Klein-en teoria Fisikaren arloan berrintegratu da eta horretarako indar-eremuen simetria Naturarengan barnekoa den egitura geometriko baten emaitza dela suposatzen da. Are gehiago, gauge simetriak dimentsio espazial berriei erantsitako geometri motak dira.

Kaluza/Klein-en teoria orokortuak bete beharko lituzkeen arazoak, ondoko hirurak dira. Lehenik, eremu fermioniko bat bete beharko du gure unibertsoan dauden fermioiak adierazteko. Baita eremu bosoniko bat (gutxienez) ere adierazi beharko luke, eta noski, eremu grabitatorioa (izkutuan dauden dimentsio kiribilduen jatorria hain zuzen). Baldintza guzti horiek betetzen dituen eredua 11 dimentsioko supergrabitatearen bertsio bat da. Beraz, Kaluza/Klein-en teoria modernoak 11 dimentsioko unibertso bat postulatzen du. Hamaika dimentsio horietatik zazpi, kiribilduak egongo lirateke maila bateraino, non behaketa zuzenarentzat izkutaturik geldituko bait lirakete.

Kiribilduak agertzen diren dimentsioei, topologi mota asko dagozkie, eta egokiena zein den aukeratzeko prozesu zehatz bat eraman behar da:

Supergrabitatearen ekuazioak ebatzi.
Ebazpide horietatik zenbait, lau dimentsio espazial-denboral eta zazpi dimentsioko forma topologiko itxiari egokituko litzaizkiekenak aukeratu.
Gero, ekuazioen ebazpideari dagokion gainazal bakoitzaren simetri multzoa aztertuko genuke.
Simetri multzoak, grabitatearekin batu behar den gauge teoria ez-abeliarra definitzen digu.
Gainazal itxi desberdinek simetri mota desberdinak dituzte, eta bakoitzak Batasun Handien Teoria desberdin bat definitzen du.

1. Bukatzeko, gainazal itxiek baimentzen dituzten uhin geldikorren egiturak aztertzen dira. Egitura horiek, teoriak lau dimentsioko espazio-denbora arruntean aurresaten dituen zatikien ezaugarriak definituko dituzte.

4.- Heptaesfera

Lor daitezkeen topologia guztietan matematikariek topologia berezi bat aukeratu dute bere ezaugarriengatik: Heptaesfera (esferaren zazpi dimentsioko baliokidea). Eredu horren bidez atomo txikienetik galaxia handienera bitarteko egitura guztiak deskribaturik gelditzen dira.

Zazpi dimentsioko esfera hau deformatzen bada, simetrien izkutatzea eta bapateko etendura ager ditzake. Arrazoi hauengatik eredu hau optimotzat hartua izan da.

Posible ote litzateke esfera hau zundatzea eta fisikoki atzematea?. Orain dela gutxi egindako kalkuluen arabera, heptaesfera honen zirkunferentziaren luzera 10 ^-32 cm koa da. Dimentsio hau, Fisikan erabiltzen den eta zentzu fisikoa duen distantziarik txikienaren ondoan kokatzen da; Planck-en distantzian alegia.

Heisenberg-en ziurgabetasun-printzipioaren arbera Kaluza/ /Klein-en heptaesfera zundatzeko beharko genukeen energi maila, protoiaren masa baino 1019 aldiz handiagoa izango litzateke. Energi maila honetan hamaika dimentsioko egitura espazio-denborala ikus genezake. Baina hori lortzeko Ortzeko Esne-bidea bezain handia den zatiki-azeleragailu bat beharko genuke.

Dena dela azkeneko urte hauetan egindako ikerketetan arazo garrantzitsuak azaldu dira eta arazo horiek askotan ez dira konpatibleak guk ezagutzen eta aztertzen dugun lau dimentsioko munduarekin. Arazo horietako bat ondokoa da: Aztertutako hamaika dimentsioko mundu guztietan neutrino destrogiro eta lebogiroen existentzia aurresaten da. Hori guk daukagun esperientziarekin ez dator bat. Gure munduan neutrino guztiak lebogiroak dira.

Lokarri edo korden forma duen partikula txiki batek, dimentsio bakarra du. Superkorden teorian, kordak guztiz txikiak dira eta 10 dimentsioko antzeko espazio eta denboran higitzen dira. Unibertsoko orrientzako superkorden teoriak dituen propietateak gaur egun asko ikertzen ari dira eta matematika kontenporaneoaren arazo garrantzitsu batzuekin harreman estua dute.

Badago beste arazo bat ere. Kaluza/Klein-en munduetan kiribilduak dauden dimentsioek beste dimentsio espazio-denboralei oso kurbadura handia ematen diete. Horrek gaur egungo behaketa astronomikoekin kontraesan ederra sorterazten du, zeren eta azkeneko hauen arabera unibertsoak duen batezbesteko kurbadura ia-ia nulua bait da.

5.- Gaur egungo perspektibak

Aipatutako arazoak eta grabitazio kuantikoaren infinituen arazoak presente egon dira azkeneko urte hauetan. Gaur egun (1985 urtean zehar egindako aurrerapenen arabera) hamar dimentsioko unibertsoaz hitz egiten da zientifikoen artean eta unibertso hori azaltzeko Superkorden teoria (1) deritzonak itxaropen handiak sorterazi ditu.

Puntu honetara helduta, erabiltzen diren gauge teoria ez-abeliarrak garatzeko hamar urte inguru behar izan zirela gogoratuko dugu. Horregatik supergrabitatearen eta Kaluza/Klein-en teorien arteko harremanak sendotzeko, seguraski zenbait urtek pasatu beharko dute. Bitartean, lan teorikoak eta teoria horiek inplikatzen dituzten matematika bereziak garatu beharko dira.

Matematika/Fisika binomioak gero eta garrantzi handiago dauka. Supergrabitatearen teoria fisikoa bultzatu zuen aurkikuntza matematikoa, zenbaki antikonmutanteena izan zen. Grabitazio kuantikoaren teoria fisikoak behar duen matematika, sortu gabe dago oraindik.

OHARRAK

Teoria berri honetan, oinarrizko zatikiak (kuantoak), bibratzen ari diren korden bitartez ordezkatzen dira. Bibrazio bakoitzari zatiki bat dagokio. Superteoria honetan korden teoria eta supersimetria konbinatzen dira.