Trece novas solucións ao problema do tres corpos

2013/03/15 Roa Zubia, Guillermo - Elhuyar Zientzia Iturria: Elhuyar aldizkaria

• Matematika
• Fisika

Newton atopou o problema cando publicou a lei da gravidade. Cando se analizan dous corpos, como una estrela e un planeta na órbita circundante, non hai problema: o cálculo do movemento é exacto. Each contains repetitions órbits on the mass centre. Pero cando se engade un terceiro corpo ao sistema, como o Sol, a Terra e a Lúa, non é posible calcular as periodicidades dos movementos do tres. Non é posible, así o demostrou o matemático Heinrich Bruns no XIX. A finais do século XX. E moito menos paira o caso no que se pasa de tres corpos a moitos corpos.

Isto significa, por exemplo, que non é posible determinar matematicamente os movementos dos planetas do sistema solar a través das ecuacións das órbitas. Sempre haberá que engadir correccións nos movementos calculados paira eles. Paira calcular cando se producirán as eclipses e desde onde se van a ver tamén é necesario realizar cálculos complexos. E fóra da astronomía tamén inflúe o problema, xa que existe a mesma dificultade paira calcular os movementos das tres partículas.

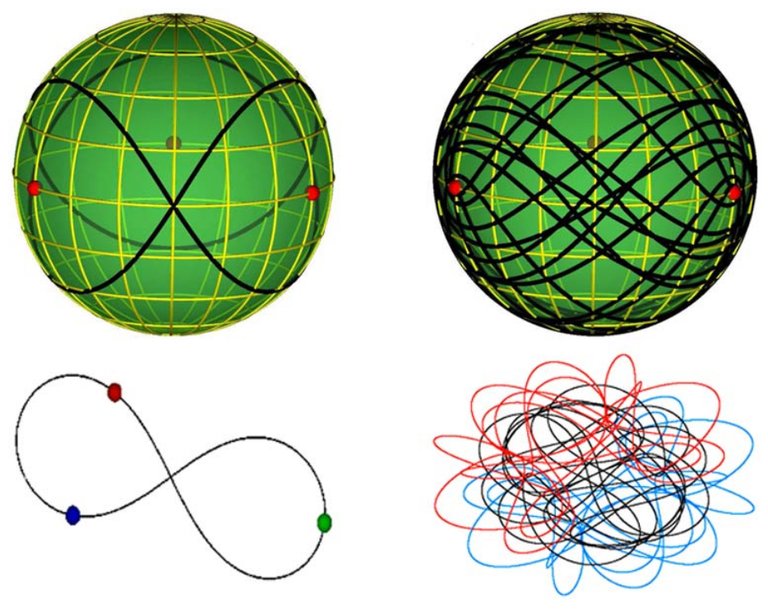
Con todo, en casos concretos e particulares pódese atopar solución. XVIII. No século XIX, os famosos matemáticos Euler e Lagrange resolveron o problema paira o caso de que uno do tres corpos tivese moi pouca masa e tendo en conta o movemento sobre unha circunferencia. Na década de 1970, o matemático Roger Brouke e o astrónomo Michel Henon calcularon una solución paira outro tipo de casos: cando uno dos tres corpos móvese en órbita ao redor dos outros dous. E en 1993, o físico Cristopher Moore atopou un terceiro tipo de solución paira os movementos ochomiles.

Até o momento, só estas tres familias de solucións foron posibles paira o problema dos tres corpos. Agora, con todo, houbo una revolución: Físicos da Universidade de Belgrado atoparon moitas novas solucións. A súa técnica consistía en partir de solucións concretas, modificando progresivamente as condicións iniciais dos movementos dos tres corpos até atopar una nova solución. Os físicos están sorprendidos porque esta técnica deu moitos resultados. De feito, as solucións que obtiveron tiveron que clasificalas en trece familias diferentes. Isto significa que xa hai dezaseis familias de solucións paira o problema dos tres corpos.