Geometrical tests

1993/06/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Pythagoras' theorem is not the only one that can be demonstrated by geometry. Many of the similarities and mathematical differences can be contrasted using geometric figures. In this article we present some of them.

The first figure shows the simple geometric verification of one of the basic formulas:

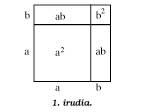
(a + b)2 = a2 + 2ab + b2

In the second figure if it is similar to the previous formula

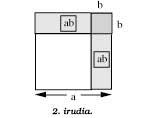
(a - b)2 = a2 - 2ab + b2

This is the geometric expression corresponding to the formula. Note that the square corresponding to the summing b2 is inside the rectangle corresponding to the adding ab and that the square a2 is removed twice ( -2ab).

If in figure 2 we extract square b2 by square a2 (figure 3), the drawn surface, 2ab, does not change. Now the following differentiation is observed:

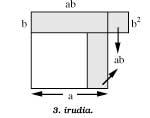
2ab a2 + b2

Continuing with the differences, figure 4 shows the geometric demonstration of another differentiation equivalent to the previous:

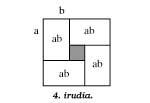
4ab (a + b) 2

Let us now calculate the sum with infinite adding (Figure 5). Adding half to the square of side 1 we get 1 + 1/2 = 3/2. Adding to this sum the fourth part of the square we have 1 + 1/2 + 1/4 = 3/2 + 1/4 = 7/4. Adding an eighth to the latter 1 + 1/2 + 1/4 + 1/8 = 7/4 + 1/8 = =15/8. As can be seen in the figure, this sum is less than 2. The following adding 1/16 can be inserted into the gap that is empty. In the gap that remains uncovered we can always include all the following Swedes. Finally we will cover the rectangle 1x2. Therefore,

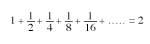
We will achieve equality. The points that appear in this equality indicate that it is infinite adding.

Passing to another formula, we will calculate the sum of the first numbers. For this purpose we will use the basic squares. (See figure 6).

If we continue like this, we will calculate the sum of the first n numbers (see figure 7).

1 + 2 + 3 + ... + n = n (n + 1)/ 2.Using basic squares we can try other formulas. Figure 8 shows us that the sums of odd numbers are square numbers.

What about even numbers?. Let's see it.

The sum of the even numbers do not form squares, but rectangles. (See figure 9).

This is the geometric expression of another new formula.

We will end with the geometrical explanation of another more complicated formula:

13 + 23 + 33 +... + n3 == (1 + 2 + 3 + ... + n)2

the formula.

Following the line of the expressions of the formulas above, we obtain the following equality:

13 = 113 + 23 = 9 = 32 = (1 + 2)213 + 23 + 33 = 36 = 62 = (1 + 2 + 3)213 + 23 + 33 + 43 = 100 = 102 = (1 + 2 + 3 + 4)2

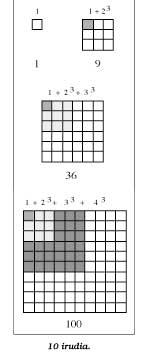
And generalizing the results would achieve this formula.