Proves geomètriques

1993/06/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

El teorema de Pitàgores no és l'únic que pot demostrar-se per geometria. Moltes de les similituds i diferències matemàtiques es poden contrastar utilitzant figures geomètriques. En aquest article et presentem algunes d'elles.

La primera figura mostra la verificació geomètrica simple d'una de les fórmules bàsiques:

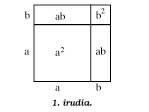
(a + b)2 ⁼ a2 + ^2ab + b2

En la segona figura si és similar a la fórmula anterior

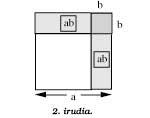
(a - b)2 ⁼ a2 - ^2ab + b2

es tracta de l'expressió geomètrica corresponent a la fórmula. Observi's que el quadrat ^{corresponent al sumant} b2 està dins del rectangle corresponent al sumant ab i que al quadrat a2 se li lleva ^dues vegades ( -2ab).

^Si en la figura ² extraiem el quadrat b2 pel quadrat a2 (figura 3), la superfície traçada, 2ab, no canvia. Ara s'observa la següent diferenciació:

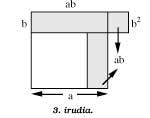
2ab a2 ⁺ b2

Continuant amb les diferències, la figura 4 mostra la demostració geomètrica d'una altra diferenciació equivalent a l'anterior:

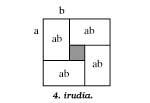
4ab (a + b) 2

Calculem ara la suma amb infinit sumant (Figura 5). Afegint la meitat al quadrat del costat 1 obtenim 1 + 1/2 = 3/2. Sumant a aquesta suma la quarta part del quadrat tenim 1 + 1/2+ + 1/4 = 3/2 + 1/4 = 7/4. Afegint un vuitè a aquest últim 1 + 1/2 + 1/4 + 1/8 = 7/4 + 1/8 = =15/8. Com es pot apreciar en la figura, aquesta suma és inferior a 2. El següent sumant 1/16 es pot introduir en el buit que està buit. En el buit que queda sense cobrir sempre podrem incloure tots els sumands següents. Finalment cobrirem el rectangle 1x2. Per tant,

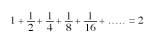
Aconseguirem la igualtat. Els punts que apareixen en aquesta igualtat indiquen que està infinit sumant.

Passant a una altra fórmula, calcularem la suma dels primers números. Per a això utilitzarem els quadrats bàsics. (Veure figura 6).

Si continuem així, calcularem la suma dels n primers números (veure figura 7).

1 + 2 + 3 + ... + n = n (n + 1)/ 2.Utilitzant

quadrats bàsics podem provar altres fórmules. La figura 8 ens mostra que les sumes dels nombres imparells són números quadrats.

Què passa amb els nombres parells?. Ho veurem.

La suma dels nombres parells no formen quadrats, sinó rectangles. (Veure figura 9).

Aquesta és l'expressió geomètrica d'una altra nova fórmula.

Acabarem amb l'explicació geomètrica d'una altra fórmula més complicada:

13 ⁺ 23 + ³³ +... ⁺ n3 == (1 + ² +
3 + ... + n)2

la fórmula.

Seguint la línia de les expressions de les fórmules anteriors, obtenim les següents igualtat:

13 ⁼ 113 +
23 ⁼ 9 = ³² = (1 + 2)213 ⁺ 23 + 33 = ³⁶
= ⁶² = (1 ⁺ 2 + 3)213 ⁺ 23 + 33 ⁺ 43 = 100 = 102 = ⁽¹
+ ² + 3 ⁺ 4)2

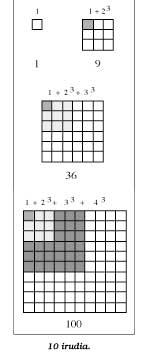
i generalitzant els resultats aconseguiríem aquesta fórmula.