Física del Renaixement
La recerca del camp que ocupa en l'actualitat la Física va tenir una època de transició en el Renaixement. Física moderna XVII. No es va materialitzar fins a mitjan segle XX, moment en el qual es va començar a utilitzar l'eina matemàtica en l'expressió i recerca dels fenòmens del món físic. Matemàtiques i astronomia XV. i XVI. A pesar que en els segles es van produir canvis bàsics (en el primer d'ells de la mà de l'abstracció en el plantejament dels problemes i en el segon del sistema copernicà), en Física no es produïa tal canvi.

Si ens fixem en el camí previ per a entendre això, és a dir, en el segle passat, apareix clarament el motiu d'aquesta diferència. Astronomia i Matemàtiques van conèixer dues obres de gran importància que van servir d'exemple per als pròxims segles en l'era clàssica, els Elements d'Euclides i els Almagesto de Ptolemeu. No obstant això, en l'àmbit de la Física clàssica no es coneixia aquest tipus d'obres. L'obra més excel·lent de la física grega és la d'Arquimedes (tant en capacitat com en el camí que més tard seguiria aquesta ciència), però no tenia en absolut el cos de les dues obres citades, ni la seva rotunditat i generalitat. A més, hem de dir: La física d'Arquimedes, bastant iniciada, era gairebé desconeguda.
En el camp de la física, com en altres mil camps, des de l'època grega fins al segle XVI. Fins al segle XX el punt de referència era Aristòtil. Aquella física era totalment qualitativa i en ella (predominant els problemes mecànics) la matemàtica no tenia lloc. Per això, saber que l'era de la Física moderna va començar amb el tractament matemàtic del moviment i les seves causes no ha de sorprendre'ns.
L'escola nominalista baixmedieval de la Universitat de París va fer una profunda crítica a la teoria del moviment aristotèlic. La resposta a aquests problemes es quedava en la teoria de l'impetus. D'altra banda, els nominalistes i abans alguns escolàstics (encara que de forma molt modesta) van introduir al món de la física, d'alguna manera, la matemàtica eina. En Aristòtil la quantitat i la qualitat eren dues categories totalment diferents i no es podia establir cap relació entre ambdues. Per a aquests pensadors medievals la qualitat era alguna cosa que es podia mesurar numèricament, és a dir, pensaven que es podia fer una gradació com el que es fa amb les qualitats, amb les quantitats.
Tradició d'Oxford
La preocupació de l'escolàstica mai era la resolució de problemes científics especials. Per contra, si alguna vegada abordaven algun problema científic, l'incloïen en un marc filosòfic general, normalment referit a un exemple i no a un altre. La seva responsabilitat era sobretot la part metodològica. No obstant això, XIV. Al llarg del segle XX es van publicar nous enfocaments per a la recerca dels fenòmens de la naturalesa que més tard resultarien prolífics en la creació de la ciència moderna. Com a exemple de tot això, tenim obres de Grosseteste, Witelo o Teodórico de Freideberg. Aquests i uns altres van tractar d'utilitzar d'alguna manera les matemàtiques per a investigar el moviment.

Com a punt de partida es troba el que avui diríem una relació funcional, és a dir, una consideració sistemàtica entre causes i efectes. Des d'aquest punt de vista, l'expressió de qualsevol fenomen es podia donar a través d'una funció algebraica, sempre que es coneguessin totes les condicions necessàries, és a dir, es reivindica la relació entre variables independents i dependents. La formulació d'aquestes relacions funcionals es va dur a terme mitjançant dos mètodes. La primera és la paraula algebra. Això ho va utilitzar Brawardino en els seus escrits sobre mecànica, en els quals utilitzava lletres de l'alfabet en lloc de quantitats variables per a obtenir generalitat, però operacions matemàtiques (suma, multiplicació, etc.) necessitava paraules expressives. Aquest mètode va collir un gran èxit a Oxford.
Una altra manera d'expressar les relacions funcionals era la de la via geomètrica. XIV. A principis del segle XX, tant a Oxford com a París, l'expressió de l'intensiu d'una qualitat estava molt estesa per coordenades directes. Un dels inventors d'aquest camí va ser el Joan de Dumbleton. En el seu llibre Summa logicae et philosophie naturalis, va realitzar tota l'expressió crítica de la física de la seva època.
XIV. Al llarg del segle XX, els científics van tractar d'expressar quantitativament canvis qualitatius i això va tenir les seves conseqüències en el camp de les matemàtiques i la física. Per exemple, per a Ockam l'única manera d'objectivar el temps era mitjançant la representació de totes les posicions consecutives d'un cos amb moviment uniforme, i basant-se en això, després podien oferir comparativament la durada del moviment de qualsevol altre moviment. Entre els metges coneixien cert escalat numèric per a expressar fred i calor. El molt estès dividia l'escalat del fred i de la calor en grups.
Totes aquestes consideracions tenen gran importància, ja que la física aristotèlica vigent en l'època es tamisava i, d'altra banda, cal tenir en compte el mal estat dels mesuradors que es podien utilitzar: els rellotges d'aigua i sorra (més tard mecànics; el rellotge de pèndol no s'inventaria fins a 1657), els instruments utilitzats pels comerciants per a mesurar esquadres, compassos, balances, longitud, volum i pesos, i només un mesurador astronòmic.

El mètode de mesurament i experimentació va passar d'Oxford i París a Alemanya i Itàlia. Un dels defensors més entusiastes d'aquest mètode era Nicola de Cusa, que ens parla de la utilització de la balança per a conèixer la proporció dels primers elements dins de metalls i esperits (mercuri, sal, sofre, amoníac i arsènic). Va proposar també com a mesurador la balança per a expressar la virtut de l'imant. Va inventar un higròmetre per a mesurar el pes de l'aire, etc.
No obstant això, els assajos de quantificació de les qualitats realitzats pels escolàstics són bàsicament diferents als de la ciència moderna. D'una banda, en els seus treballs teòrics no apareixen dades reals, és a dir, l'aplicació de les matemàtiques no prové de l'observació, sinó de l'elubración. D'altra banda, la tendència a la seva generalitat els induïa a preocupar-se de la lògica per sobre de tot i, de pas, a realitzar extrapolacions més absurdes. Per tant, el fet que tot això sigui considerat pioner de la ciència moderna té el seu problema. No obstant això, la influència d'aquesta metodologia en la posterior ruptura epistemològica no és negable.
Escola Impetusa
Aquesta teoria va aparèixer i es va estendre entre els pensadors d'Oxford, però la seva formulació completa i desenvolupada la va obtenir més tard a París i finalment el XVI. Fins a gairebé finals del segle XX va ocupar el seu lloc en totes les universitats europees. Cal dir que el Leonardo da Vinci, per exemple, que s'ha utilitzat com a arquetip de la ciència renaixentista, era esclau d'aquesta teoria i que en altres ocasions, quan els historiadors han considerat les aportacions especials d'aquest home a la teoria del moviment, s'ha vist que, en la majoria dels casos, són adaptacions dels escolàstics parisencs. D'altra banda, és clar que els treballs sobre el moviment juvenil de Galileu estan relacionats amb aquesta escola.
Els escolàstics van trobar sobretot en les seves tesis aristotèliques de moviment dues dificultats: el moviment de projectils i peces pesades. Per a Aristòtil i els seus seguidors, a diferència del que avui és degut a la inèrcia, la causa era el moviment i no la inactivitat. Per tant, perquè un cos tingui moviment ha de tenir una causa motriu en contacte físic i sense interrupcions. La interrupció d'aquesta causa motriu o impulsora comportarà l'anul·lació del moviment. D'altra banda, admetien que si l'obstacle que contraposa al mòbil l'interval persisteix constant, la seva velocitat dependria de la força que se li imposi. Per tant, com podem expressar l'acceleració que s'observa en la caiguda de peces amb pes? Per què la fletxa no cau a terra tan aviat perd contacte amb el cordó de l'arc? Entre la teoria i el que es veia hi havia un gran forat.

Els seguidors d'Aristòtil expressaven d'alguna manera aquestes discrepàncies. Per exemple, per a expressar el moviment continu dels projectils s'acceptava el canvi produït per l'embranzida inicial en l'aire, és a dir, a mesura que s'impulsa i comprimeix l'aire que precedeix a l'extrem, es passava ràpidament cap endarrere i s'impulsava el projectil perquè no es produís cap buit en l'aire (una cosa inacceptable per a ells). Tant Leonardo da Vinci com els seus guarnicioneros de l'època admetien aquest culte. A l'hora d'expressar el moviment de les peces que pesen, i veient que es tracta d'un moviment accelerat, utilitzaven un altre argument basat en l'aire, és a dir, com més a prop està el cos de la superfície, major és el pes de l'atmosfera sobre ella i menor és l'obstacle de la columna d'aire que hi ha sota ella. Per tant, el cos s'accelera.
La crítica més profunda a aquesta teoria del moviment (va haver-hi unes altres abans i després) va ser la XIV. Van ser creats a Oxford i París en el segle XIX. Aquesta és la de Joan Buridan, rector de la universitat de París en dues ocasions. En dos llibres, Quaestiones super octo llibres physicorum i Quaestiones de coelo et món, va plasmar la seva teoria. Aquesta teoria parteix de la necessitat d'un motor per al moviment, per la qual cosa, d'alguna manera, pot considerar-se com el desenvolupament final de la teoria aristotèlica.
L'impeto era una peculiaritat que els cossos rebien per estar en moviment. L'impeto en els projectils va disminuint constantment, tant per la molèstia de l'aire com per la gravetat cap al sòl. En el cas de les peces de pes , l'impetus era una mica com la gravetat que se solapava pel moviment. Així, la seva acceleració era conseqüència de la suma d'impetus consecutius. Consideraven que l'impeto de qualsevol cos era el producte de la seva quantitat de materi per la seva velocitat.
Entre altres coses, el mèrit d'aquesta teoria és expressar-se mitjançant una sola dinàmica d'agarri o de terra.

Aquest camí d'anàlisi va tenir el seu reflex en el Renaixement. Nicola de Cusa, per exemple, apareix com el seu seguidor i Leonardo da Vinci o Kopernik. Cardano, en el seu treball De subtilidad (1550), no del tot, l'accepta en part.
Ciència i tècnica
Al llarg dels segles medievals es van establir les bases sòlides del canvi tecnològic, però el medi ambient econòmic, filosòfic o social no era el més adequat per a la seva materialització. Tant el creixement del comerç com el desenvolupament de la burgesia serien el motor d'aquest corpus i de la creació del món modern. B. Com va dir Gille: XV. A la fi del segle XX es va convertir en tècnica una de les principals activitats de la societat moderna. Per descomptat, les relacions entre la tècnica i la ciència eren escasses.
No obstant això, l'ambient anava canviant. XIII. En el segle XX Roger Bacon va escriure: Si pogués, cremaria tots els llibres d'Aristòtil. Estudiar no és perdre temps, sinó conduir cap a l'error i augmentar el desconeixement. I més tard: llevar-vos de la mà dels dogmes i del mandat de les autoritats: mireu el món. Pot pensar-se que en el seu moment aquest missatge revolucionari no va tenir cap èxit. No obstant això, indica la tendència d'un corrent. En el quattrocento, per exemple, l'inacceptable del segle passat trobaria un ambient molt més adequat i per a entendre-ho cal tenir en compte els canvis socials que s'han produït, entre ells la conjugació entre ciència i tècnica.
A la Grècia clàssica existia una enorme oposició entre les arts liberals (és a dir, les que practicaven els homes lliures) i les arts mecàniques (és a dir, les que usaven els esclaus). Aquesta actitud va perdurar durant l'Edat mitjana. Mentre que els teòrics (és a dir, filòsofs o teòlegs o professors universitaris) gaudien de gran prestigi i prestigi, els pràctics (artesans o enginyers o arquitectes, és a dir, aquells que utilitzen les seves mans o que tenen les seves obres directament relacionades amb la producció) es troben en un nivell molt més baix, encara que no es rebien amb menyspreu.

Aquesta situació va sofrir un profund canvi en el Renaixement. Tècnics de la mineria, arquitectes, rellotgers i tots els artesans van ser rebuts amb respecte pel poder que tenien per a dominar la naturalesa. Per això, les arts mecàniques van passar a primer pla en sintonia amb les obres teòriques. En aquest sentit, alguns teòrics van tractar de defensar o enaltir les arts mecàniques i uns altres de lluitar contra la mera situació teòrica. Bernard Palissy, per exemple, conegut ceramista parisenc, va publicar en 1580 el seu Discours admirables, on es poden trobar mil raons contràries a la cultura que llavors s'ensenyava a la Sorbona.
Va reivindicar que la veritable filosofia és només l'art de l'estudi de la naturalesa, és a dir, alguna cosa que tots (i no sols els filòsofs o teòlegs) podem fer. Com Palissy podem citar a Rabelais, Luis Vives o Andrea Vesalius del mateix segle. Tots ells, sense excloure els estudis teòrics (sinó a l'inrevés), es van decantar per activitats tècniques, és a dir, pel coneixement positiu enfront de la mera especulació o a la pràctica literària, rebutjant d'alguna manera el concepte de ciència d'Aristòtil. A partir de llavors les noces que es va produir en aquest segle donaria els seus fruits fins ara.
Moviment i estàtica
XVI. A causa del desenvolupament de la indústria d'armes de foc en el segle XVIII, l'antic problema dels projectils va tornar a aparèixer, però aquesta vegada plantejat des d'una perspectiva pràctica. Mentre milloraven les seves petites armes, va començar la fabricació de canons de gran calibre a Alemanya. Les armes petites no tenien problemes teòrics, però a mesura que les grans tenien major potència, produïen problemes de punteria. En 1537 Tartaglia va publicar el llibre Nova sciencia, una nova ciència que no era més que una balística. A través d'aquest llibre pretenia adaptar l'expressió teòrica al que encara era un saber empíric.
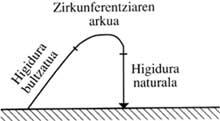
Al marge de la filosofia (que va escriure el llibre per al seu ús per part dels tècnics), aborda el treball a través de les matemàtiques. Tartaglia presa un camí euclidià: al principi posa uns axiomes i uns supòsits i d'ells extreu algunes conclusions per a la recerca dinàmica dels projectils. No obstant això, la mecànica que utilitza és l'habitual. Per això, el moviment pot ser natural o forçat i la caiguda lliure és l'únic moviment natural existent. En el moviment natural la velocitat del mòbil augmenta a mesura que s'allunya del seu origen o s'acosta a la seva destinació. En el moviment forçat succeeix exactament el contrari. La diferència intrínseca entre aquests dos tipus de moviment fa que es consideri impossible que es produeixin simultàniament. Per tant, el moviment natural s'inicia immediatament després de l'embranzida i és tangent a aquest. Encara que no es correspon amb el que s'ha dit i amb les observacions, dibuixant la trajectòria dels projectils mostra tres fases: dos recorreguts rectes units per un arc de la circumferència.
Gairebé deu anys després va escriure un altre llibre: Onestiti et inventione. En ell, quan analitza el moviment dels projectils, quan no és vertical, accepta com a corba el recorregut de tots els moviments impulsats. No obstant això, aquest punt de gran importància no va ser pres amb atenció.
Al marge del moviment, en 1586 ens trobem amb Estàtica. Aquest mateix any Simon Stevin va escriure sobre l'estàtica en holandès el seu llibre De beghinselen der weeghconst sobre les aplicacions i una mica després un altre sobre les aplicacions i després el tercer sobre la hidrostàtica.
L'estàtica es divideix en dos llibres. En ell s'investiguen les propietats de l'equilibri entre els pesos i els centres de gravetat d'imatges planes i sòlides. Al principi, després de donar algunes definicions i postulats, investiga el cas de certs pesos (per a entendre la palanca) que tiren verticalment. Posteriorment explora el cas de les forces inclinades introduint el pla inclinat. De la recerca d'un conjunt de pesos, units per un cordó i penjats d'un prisma triangular, va sorgir la idea d'un paral·lelogram de força, que posteriorment va ser utilitzat en màquines complexes.

En el camp de la hidrostàtica, Stevin ens va donar els seus primers assoliments des de l'època d'Arquimedes. Després de comprovar que els líquids estan en equilibri, independentment del seu diàmetre, en els recipients comunicats, va comprovar que la pressió sobre el fons només està relacionada amb l'altura del líquid. Posteriorment s'encarregaria de la pressió dels murs laterals, incloent el cas dels murs corbs.
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian











