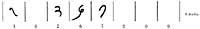Com operar? (II). Multiplicació i divisió

1990/11/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Multiplicació

Quant a la multiplicació, cal esmentar un cas especial (que té com a producte el número 10). En el producte manual esmentat anteriorment, es deia que els dits que baixaven a les mans es multiplicaven per 10 (mentalment). Dins d'aquest capçal està: el nombre de dits que baixen ens dóna la desena part del producte.

Els egyptianos també sabien multiplicar per 10. Després d'escriure un número per a això, cada símbol d'un ordre era substituït per un símbol d'ordre següent (figura 1).

En el sistema de numeració xinès també es pot veure el testimoni d'aquest cas. Depenent del lloc on es posi el símbol 10, pot tenir dos significats diferents (figura 2): si es col·loca a l'esquerra dels símbols d'altres números més petits, es té suma. Si s'escriu a la dreta significa multiplicació.

Vegem com es realitzaven altres multiplicacions.

Els egypti escrivien 1 i el producte més petit en la part superior de dues columnes. Després es doblegaven consecutivament aquests números i s'escrivien sota. Els doblatges es feien fins que en la columna 1 s'obtenia l'altre producte (no el menor) o, si no ocorregués, fins que aparegués el número més gran que l'altre producte. En el primer cas apareixeria el resultat al costat de l'altre producte, en la columna de la dreta. En el cas a) de la figura 3 s'obté el producte 128 x 12 = 1536. En el segon cas, en la columna de l'esquerra (columna 1) se seleccionaven els números que sumaven el major producte. El resultat s'obtenia sumant en la columna de la dreta els números corresponents als números anteriors. En el cas b) de la figura 3 apareix el producte 369 x 19 = 4864 + 1216 + 608 + 304 + 19 = 7011.

La multiplicació egyptiana era, per tant, implea i no necessitava taules. Però no va ser l'únic mètode utilitzat pels egyptianos. També utilitzaven el mètode denominat desdoblament. En aquesta ocasió els dos productes s'escrivien al cap de dues columnes, calculant la meitat de la més gran (menyspreant les restes) i les dobles de la més petita i col·locant-les en les columnes corresponents. En la columna de parells es van sumar els corresponents als nombres imparells de la columna de mitjanes, obtenint el producte. En la figura 4 es pot veure el producte 54 x 37 = 74 + 148 + 592 + 1184 = 1998. Aquest mètode també apareix en alguns països de la Unió Soviètica.

Els hindús usaven un àbac de columna en sorra. En aquest àbac, en la columna de la dreta, escrivien les unitats; quan estava a la seva esquerra les desenes; els percentatges a la seva esquerra, etc. Deixaven en blanc per a indicar la falta d'unitats (figura 5).

Aquest àbac s'utilitzava per a realitzar les multiplicacions. Per exemple, per a calcular el producte 325 x 28 s'escrivien en un àbac de quatre columnes, el major en la part superior dreta i el segon en la part inferior esquerra. En el primer pas, calculaven (3 a dalt) per (2 a baix), 6 i escrivien en la columna esquerra del 3. A continuació (3 a dalt) per (8 a baix), 24, i en comptes de 3 escrivien 4 i afegien 2 al 6 anterior.

El primer pas ja havia finalitzat. Abans de començar el segon, el número inferior es movia per una columna cap a la dreta. Ara (2 a dalt) es calculava per (2 a baix), 4, i s'afegia a la 4 anterior (a l'esquerra de la 2 superior). Després (2 a dalt) per (8 a baix), calcular i substituir el 2 per 6, eliminant el 2 i sumar 1 al 8 que estava a la seva esquerra. Així acabava el segon pas i una columna amb el número inferior cap a la dreta. En el tercer pas (5) per (2 inferior), calcular 10; se sumaven 0 i 6 (5 esquerra) i 1 i 9 (6 esquerra), sent el primer 6 i el segon 10. Així, a la 8 (a l'esquerra del 9) se li sumava 1, sent el número superior 9065.

Després (5 a dalt) per (8 a baix), calcular; escriure 0 en comptes de 5 i afegir 4 al 6 (a l'esquerra del 5) obtenint 10; escriure 0 en lloc del 6 i sumar 1 al 0 (a l'esquerra del 6) per a obtenir 1. Aquí finalitzava el tercer i últim pas, sent el número superior 9100. Això era precisament el producte. Una nota: quan nosaltres escrivim 0 ells van deixar la columna buida (figura 6).

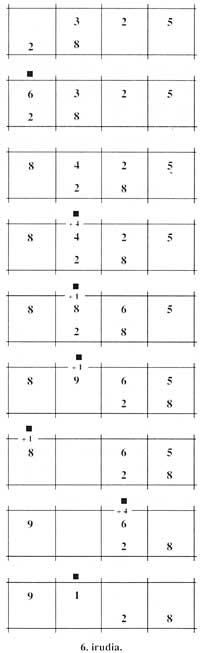
En resum, podem escriure:

Però aquest mètode era llarg i molest. Quan van trobar el zero, van deixar d'utilitzar l'àbac i les xifres van prendre el valor segons el lloc. Això va facilitar el càlcul de les operacions als matemàtics hindús.

Heus aquí com es va multiplicar a partir del segle V. Es tracta de l'anomenat mètode de quadrícula, al qual els europeus van denominar per gelosia (saretazko).

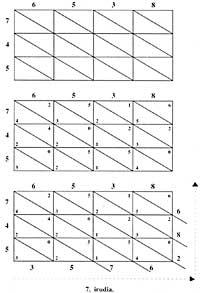
Suposem que volem multiplicar 6358 x 547. Com el multiplicador 4 té 3 xifres, dibuixem un rectangle de 4 columnes i 3 files. Els números s'escriuen en la capçalera de les columnes i files respectivament. Dividim cada casella per una diagonal que uneix el vèrtex superior esquerre amb l'inferior dret.

En cadascuna de les caselles, una vegada multiplicats els números que hi ha en les columnes i als caps de la fila, sent aquest producte menor de 100, s'escriu la xifra de les deu en la meitat inferior i la de les unitats en la meitat superior; per a la falta d'unitats i desenes s'escriu 0. Fora del rectangle i partint del vèrtex superior dret, en el nostre cas des del 6, se sumen els números situats entre les diagonals. Si una d'aquestes sumes parcials tingués dues xifres, la decimal s'afegiria a la següent suma i només escriuríem la de les unitats. El resultat es llegeix d'esquerra a dreta i de baix a dalt (figura 7).

Divisió

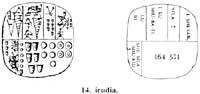
És sense llavis l'operació més complicada i inclou totes les altres. Abans d'explicar les divisions escrites, veurem una divisió de fa 46 segles. De fet, avui al poble de Fara de l'Iraq, però en el de C. El Shurupp de 2650 es va dur a terme a la ciutat sumèria. Encara que en aquella època existien les xifres sumerianas, per a realitzar les operacions utilitzaven els antics calculi. Recordem com eren les calculi:

Diverses persones van repartir un graner amb 7 silas ordis. Calia buscar el nombre de persones i la quantitat d'ordi sobrant. Un graner valia 1.152.000 silas. Per tant, l'operació a realitzar era d'1.152.000 per 7. Mentre el quocient ens donaria el nombre de persones, la sorra ens donaria l'ordi sobrant.

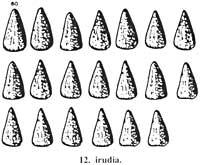
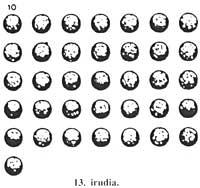
Per a representar 1.152.000 silas es van perforar 32 esferes. De fet 32 x 36.000 = 1.152.000. Les esferes perforades es van col·locar en quatre files de 7 columnes (Figura 9), sobrant quatre esferes perforades. D'aquí van obtenir 4 x 36.000 persones i 4 x 36.000 en excés d'ordi. Les quatre esferes perforades van ser substituïdes per 40 esferes (una esfera perforada tenia el valor de 10 esferes). Les 40 esferes van ser col·locades en cinc files de set columnes i 5 sobrants d'esfera (Figura 10).

Així que 5 x 3600 més i ara 5 x 3600 més d'ordi. A canvi de cinc esferes es van obtenir 30 grans cons perforats (una esfera tenia el valor de 6 grans cons perforats); 30 grans cons perforats formaven quatre files de set columnes i quedaven dos sobrants. És a dir, tenien 4 x 600 persones més i 2 x 600 silas sense repartir ordi (Figura 11). Els dos grans cons perforats van ser substituïts per 20 grans cons (un con gran perforat = deu cons grans) que també es van col·locar en dues files de 7 columnes, obtenint 2 x 60 més i deixant 6 x 60 silas sense distribuir (Figura 12). A canvi d'aquestes últimes es van prendre 36 boles (un con gran = sis boles) i es van col·locar en cinc files de set columnes, amb una bola sobrant i 5 x 10 persones més (figura 13). Finalment, substituint la bola per deu cons i formant amb ells una sola fila, és a dir, un amic més, i obtenint la resta final 3 silas ordis (Figura 14). En resum, 4 x 36.000 + 5 x 3.600 + 4 x 600 + 2 x 60 + 5 x 10 + 1 = 164.571 persones i 3 silas ordis. Una vegada realitzada l'operació, el resultat s'escrivia en una taula amb xifres (figura 15). Quant a la divisió escrita, els egyptianos utilitzaven un mètode similar a l'utilitzat en la multiplicació. 1476 dividit per 12 divisions, com si es tractés d'una multiplicació, 1 i 12 en dues columnes i sota cadascuna d'elles escrivien dobles (figura 16), fins que en la columna del 12 apareixia el major doble o el mateix número 1476. Llavors en la columna de la dreta es marcaven els números que sumaven 1476 i sumaven els números de la columna de l'esquerra als quals corresponien.

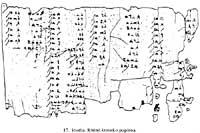
És a dir, 1476 : 12 = 64 + 32 + 16 + 8 + 2 + 1 = 123. Lògicament, per a poder dur a terme aquest tipus de divisió, la divisió ha de ser exacta. No obstant això, els egyptianos coneixien una laboriosa tècnica de divisió inexacta. De fet, els egyptianos coneixien fraccions unitàries i les utilitzaven per a calcular quocients 2/n. En el papir Rhind (figura 17) apareix una taula de descomposicions dels quocients 2/n, sent n imparella i de 5 a 101.

Canviant a temps, el mètode utilitzat a Europa abans de 1600 era el mètode de pèrdua o eliminació. A continuació, utilitzant la divisió 1556 : 42, veurem en què consistia el mètode:

L'èxit d'aquest mètode es deu a la facilitat d'ús en l'àbac sobre sorra.

XV. En el segle XVIII es crea un nou mètode de divisió anomenat adanda. Amb la paraula adanda (donant) significa, la seva causa està en el propi algorisme. De fet, quan es lleva el producte parcial es baixa la següent xifra i es dóna a la sorra. A continuació podem veure un exemple de l'algorisme d'adanda. Aquest mètode és, sens dubte, el pioner d'avui.