Time measurement
1986/08/01 Arregi Bengoa, Jesus Iturria: Elhuyar aldizkaria
Speaking of the appearance of the seasons in the previous issue, we try to unravel the cause and the most important particularities of the phenomenon. Although day and year were frequently mentioned, their duration was not analyzed. The measurement of time will be the basic problem of astronomy that we are now going to try to analyze and next time we will deal with the details of the organization of the calendar we use in the West.
The periodic movements traditionally used to measure time have been the Earth's turn, its translation around the Sun and the translation into the Earth of the Moon. Thus, day, year and month have been considered as units of time respectively. Let us now try to define these concepts more precisely than we use daily.
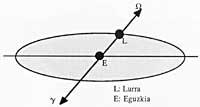
As expected, we need some references for time measurement. One of them will be the aries point defined below. This point of Aries, also called spring, is known, as we shall see, for being related to the beginning of spring in the northern hemisphere. Specifically, the Aries point is the point we get by projecting the center of the Sun into the kneading when this phenomenon occurs. (See figure 1). The other end of this straight line, the autumn one, is the pound or the euro point.
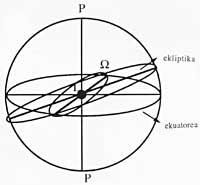
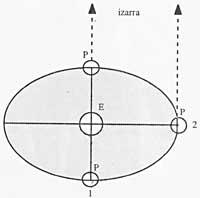
However, the analysis of the problems in which the Earth and the Sun intervene is usually done not using the system that we have represented in the first figure, but the geocentric system. As can be seen in Figure 2, the Earth will be considered in the center, with the vertical turning axis and the kneading equator. From this point of view, the Sun is the projected mass that, forming the Ecliptic, we see moving around the Earth throughout the year. As we know, when spring and autumn begin, the Sun is therefore above the equator, and euro points are the cutoff points between the equator and the ecliptic.
the reason why aries is called to the point is historical. When they were called zodiacal constellations (i.e., constellations surrounding the ecliptic at the mooring), about 2000 years ago, the point (i.e., the Sun on spring day) was in the constellation of Aries. That is why it is called. Anyway (it must be said) the point moves in the kneading and is currently in Pisces, although in general it is said that spring begins when the Sun enters Aries regardless of this change.
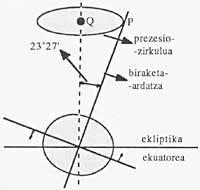
The movement of the equinoxes mentioned (precession of the equinoxes) is due to the Earth being trodden at the poles. This oppression increases radio in the equator. Therefore, the attraction of the Moon and the Sun lead the equator to join the ecliptic, with an angle of 23°27" that tends to decrease. On the other hand, instead of the pole holding the direction, it describes a previously mentioned angle cone around the junction of the ecliptic, as does the axis of a spinning top when it will finish the movement (see figure 3). The movement period is about 25,770 years. This is an annual movement of 50.29". By changing the equator plane with the pole, the point also moves 50.29" a year.
Therefore, we can start to differentiate the start-solar day. If we use a star as a reference to measure the duration of the Earth's turn, then we are limiting stardom. That is, the starry day is the time it takes a star to travel two consecutive steps above the meridian of a point. The sunny day is the one obtained by taking as reference the Sun.
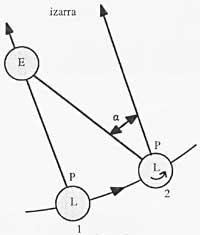
As can be seen in figure 4, this second day is somewhat longer than stardom. Suppose the star chosen to measure the starry day, the Sun and Earth are aligned at a given time and the first two are located at the meridian corresponding to the P point of the Earth. The Earth, having reached 2 points by translation and turning motion, being the star in infinity, would occupy the meridian of point P, but would have to turn a little more so that the Sun was on the P.
Although in astronomy the star day has several uses, in our daily life we must use the sunny day. Otherwise, night and day would not go with light and day would not always start at midnight. We will understand this problem with the help of Figure 5. Suppose the Earth is at point 1. At that time at point P begin the star-sunny day, that is, they are 0 and it is noon. As the months pass the two days go out and when the star day has to start in 2 positions, the Sun rises. After half a year, the start of the star day, the 0, occurs at midnight. As we have said, the official time should be based on the solar day.
However, the sunny day is also not the most suitable for measuring time, as it is not always the same. As is known, the speed of Earth's translation is not always the same, it is greater in perihelion. According to Kepler's second law, the radio vector must occupy the same surfaces in equal times. Therefore, the arc that circulates one day when the Earth is in the perihelion is greater, so the angle and the day is also greater. To overcome this problem we define a sunny day medium, always equal and divided in 24 hours. So things, the starry day has an average of 23 h 56 m 4,09 s.
Hours of astronomical phenomena are usually performed with universal time (UT). The universal time is the time with respect to the sun of Greenwich, that is, subtracting one or two official hours, according to the time of the year.
Let us now look at the types of years. As when defining the day, we must set the references first. If we take as reference a fixed star, we get the starry year: The time it takes for the Sun, Earth and star to occupy the same relative position in two consecutive periods, that is, the time it takes the Earth to form a 360° angle around the Sun. The tropic year is defined in the same way, but taking as reference the point.
The tropic year is a little shorter than stardom because the precesion moves the point in the opposite direction to the movement of the Sun. That's why the Sun, upon completing the tour, finds point 50.29" later. Specifically, the star year lasts 365 days 6 hours 9 minutes and 10.1 seconds and the tropic 365 days 5 hours 48 minutes and 47.5 seconds.
For the elaboration of the calendar is used the tropic year, which accompanies the seasons. The use of a starry would be a preview of the stations of about 20 minutes each year and a gap that would accumulate over the centuries, as is the case of the organization of agricultural work.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia