Unidades de tiempo en la antigua India

1992/06/01 Ruiz-Larrea, Isabel - Irakaslea eta ikertzaileaFisika Aplikatuko Saila II, EHU | Igartua, Josu Mirena Iturria: Elhuyar aldizkaria

• Fisika

La definición del tiempo actual (milenio, año, trimestre, bimestre, mes, semana, día, hora, minuto, segundo y sus múltiples y submúltiples) puede suponer que se han definido con gran precisión utilizando conceptos y normas específicas y universales fijadas de forma natural. La unidad de tiempo utilizada en el sistema internacional de unidades es de segundo, y una vez definido éste, el resto de unidades se han fijado de forma única utilizando sus múltiples variables.

Sin embargo, estas unidades no son las únicas unidades que pueden definirse, y puede resultar interesante observar la existencia de una cultura en la que la unidad de tiempo mencionada no se ha definido de la misma manera.

En el observatorio astronómico de Jaipur se pueden encontrar sofisticadas herramientas para determinar con precisión el tiempo. Las primeras referencias a las unidades de tiempo fueron escritas en verso sanscrítico a. C. 1200 a 600.

Si lo hemos hecho (I. R. L.) En nuestro viaje a la India nos sorprendió que los hindúes tenían conocimientos sobre la astronomía que les habían venido desde antiguo. El observatorio astronómico de Jaipur nos impresionó sobremanera, viendo el conjunto de analizadores sorprendentes que se pueden utilizar para calcular la hora local con una precisión de hasta dos segundos, tanto la ubicación de los astros como de los planetas, cuando la medición se realiza en un reloj solar gigante. Varios temas sobre los analizadores del observatorio “Elhuyar. Se publicó en el número 58 de la revista “Zientzia eta Teknika”.

Lo que más nos sorprendió es la habilidad demostrada para calcular con precisión el tiempo. La sorpresa se acentuó cuando nos dieron cuenta de que las unidades de tiempo utilizadas por los hindúes a lo largo de los años también fueron cambiando a lo largo del tiempo. En este artículo hemos decidido hacer una recopilación de las unidades de tiempo utilizadas por esta cultura. También analizaremos los equivalentes al sistema unitario actual y algunos derivados de sus denominaciones.

Equivalentes actuales de unidades de la antigua India

No cabe duda de que medir el tiempo de forma precisa para la cultura de la India sigue teniendo una importancia cultural. Se cree que la importancia de la astrología proviene de la prehistoria. A medida que las tribus se agrupan en reinos y crecen, su gobierno se hizo más complejo, aumentando el poder y la influencia de los astrólogos.

Vavaha Mihiira, grandes astrólogos, d.C. Quien vivió en el año 500, afirmó en sus escritos que al astrólogo no le honraba que el rey era un desastre, y que un único astrólogo no podía compararse con cien elefantes ni con cuatrocientos caballos.

Los conocidos de estos expertos han aparecido en varios libros en los que se han explicado las normas precisas para llevar a cabo mediciones temporales y los datos para llevar a cabo algunos ritos y sacrificios. Especial importancia tenían las determinaciones del tiempo y los procedimientos para calcular los detalles correspondientes. Los occidentales estamos acostumbrados a realizar mediciones en unidades que pertenecen a nuestra cultura y están universalmente consolidadas. La determinación exacta de las unidades de tiempo es actualmente posible y esta información es útil en cualquier punto del mundo. La unidad básica en el sistema internacional es el segundo. Los 60 segundos completan un minuto, 60 minutos por hora y 24 horas por día. Tenemos unidades más amplias: semana (7 días), mes (30 días), año (365 días), milenio, etc.

Un único elefante puede transportar al conductor y a cuatro turistas. Tampoco se pueden comparar tejidos elefantes con un solo astrólogo.

Sin embargo, las unidades mencionadas no son unidades únicas y han sido modificadas a lo largo de la historia. En el caso de la India, las unidades de tiempo eran muy diferentes. Hemos decidido analizar cuáles son las unidades, sus nombres y los procedimientos de medición y cómo consiguieron transmitir conocimientos de un país a otro. Para ello se han obtenido una serie de datos procedentes de diferentes fuentes que han fijado equivalentes a unidades de tiempo y sistemas actuales.

El manuscrito más antiguo referenciado, el Vedanga Jiotisa, está escrito en verso con sanscríticas, y a. C. Desde 1200 hasta 600 años. Siguiendo la costumbre de entonces, el maestro (que era guru) enseñaba verbalmente al alumno (que era el shishia) los conocimientos que él tenía para que el segundo aprendiera de memoria. Para facilitar el trabajo se escribieron en verso.

La primera unidad de tiempo que se menciona es el ciclo de 5 años (juga), que se inicia en la Luna del Límite (enero-febrero) y termina en la Pausa (diciembre-enero). Al año corresponden dos partes (ayana) formadas por 183 días (savana divasa), en las que el día (nitemeron) es el intervalo entre el amanecer y el siguiente.

Nos referiremos a las divisiones de tiempos correspondientes a intervalos inferiores a la fecha. Referencias conocidas, a.C. Son de 1200 a 1030 años y muchas veces no coinciden en la forma de designar o definir la unidad de tiempo.

La recopilación de estos datos se presenta en la siguiente tabla.

Caídas del nivel de agua correspondiente a diferentes recipientes utilizando el reloj de agua. a) recipiente cilíndrico, b) recipiente semiesférico (sombrero).

En general, en algunas definiciones podemos encontrar características comunes. Se explica a continuación. Todos tienen un tiempo equivalente en el interior de un día o veinte horas (nitemeron). El día se ha dividido en sesenta números (nadi, nadika, gati, gatika, danda, fecha), siendo la unidad de tiempo resultante de veinte minutos. Asimismo, la unidad de tiempo mencionada se ha dividido en sesenta tramos, alcanzando una unidad de tiempo de veinte segundos (vinadi, vinadika, pala, cashaka). Han definido como unidades pequeñas el tiempo necesario para pronunciar la respiración, o la palabra diez sílabas (gurvak-shara), en la que la unidad de tiempo coincide con la sexta parte de lo anteriormente definido.

Por lo tanto, su valor es de cuatro segundos. Como dato curioso, se puede decir que el número de pantanos al día es igual al número de minutos en la circunferencia. La relación no es tan accidental como parece. No olvidemos que la forma más utilizada para medir el tiempo en la India era el reloj de sol con la proyección correspondiente a la sombra sobre el sol.

La consolidación de unidades inferiores a cuatro segundos era muy difícil, entre otras cosas, porque sus caminos no eran fáciles de reconstruir. En eso consiste la diferencia entre los valores de las citadas unidades de tiempo.

Relojes de agua

Los tiempos cortos, como el prasta, se midieron usando relojes mecánicos de agua en lugar de basarse en observaciones de movimientos de estrellas como el sol. El ritual hindú sólo necesitaba tiempo absoluto fijado por la astrología y correspondiente a los asentamientos estelares y planetarios. El rito también necesitaba un reloj que regulara la sucesión de sacrificios. Para cumplir este objetivo se utilizaron relojes de agua (denominados Jalaiantra).

La forma más sencilla, equivalente a la clepsida helénica, era en un recipiente con agua con un pequeño agujero en el fondo. Recordando las palabras de Al-Biruni:

“Leyendo en el libro Surdava de Uptala de Kaxmirko: en la parte de la madera el hueco perforado con un diámetro de doce dedos y una altura de seis dedos tiene tres manas de agua. Si en el fondo del hueco se produjera un agujero tan grande como seis pelos de mujer joven, ni anciana, ni niña, las tres mangas de agua caerían en un conflicto a través del agujero.”

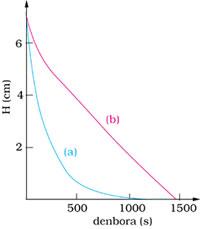
Los astrólogos actuales considerarían inadecuado este reloj, ya que, aparte de los efectos de la tensión, el nivel del agua del envase va disminuyendo según la siguiente ley exponencial:

H = H0 exp(-ct),

El reloj solar gigante o Samrat Jantra consiste en la sombra correspondiente a la proyección del goniómetro (muro triangular). La foto se tomó por la tarde.

donde c, además del diámetro del orificio, está relacionado con otros factores, como la densidad del agua y la viscosidad. El envase se vaciaría en un tiempo infinito. Debido al efecto de la tensión superficial, el flujo se corta con un pequeño volumen de agua sobre el hueco.

Dado que el detalle de la medida tiene una dependencia inversa de la pendiente de la curva correspondiente al fluido expulsado, finalmente los cronógrafos hindúes deberían abandonar este procedimiento.

En lugar de hacer lo anterior y a diferencia del reloj de agua egipcio, en el que el tiempo de caída del fluido se realizó mediante la lectura correspondiente al nivel alcanzado por el agua en el interior del recipiente, el agua caída se almacenaría en un recipiente de volumen exacto (una prasta). Al ser prasta le interesaba medir ese tiempo sólo para sus celebraciones, aunque se trataba de una unidad de volumen, se convirtió en una unidad de tiempo. Se cree que el nivel de agua que había en el recipiente se mantendría constante y a la altura adecuada.

Este reloj mejoró a lo largo de la historia y parece ser que la nueva versión fue muy utilizada en la XII. Desde principios del siglo hasta la aparición de los relojes mecánicos europeos. El envase utilizado (gatis) dio nombre al intervalo de tiempo que definió. Al parecer, el gati, equivalente a la nadika anterior y con una duración de veinte minutos, sustituyó al prasta.

d. C. En la pasada Suria Sidanta escrita por Ranganata hacia 1603 se han determinado las dimensiones del envase: “El barco era una semiesfera (capala) con una altura de seis dedos (angula) y el doble de esta medida en el borde, con una capacidad de sesenta palas de agua. El agujero de fondo era capaz de atravesar una longitud de cuatro dedos y una aguja de oro de tres mashas y un peso de un tercio.”

A lo largo de los años los sistemas de peso y medida han cambiado de valor y denominación, siendo interesante conocer el equivalente a la medida actual en cada caso. Teniendo en cuenta que el valor de la longitud desde el dedo gordo de los hindúes hasta el menor con la mano abierta era de 22,8 cm, se puede decir que el valor de la angula es de 1,9 cm. Una vez calculado el volumen del envase se puede concluir que:

1 pala = 51,7 cc

o,

1 pala = volumen = 1/2 1/4{ r360

donde r = 11,4 cm.

Por otra parte, en el caso de la antigua Varaha Mihiira, el sistema de peso se basa en la semilla de mostaza y en un grano de arroz ocho veces más pesado. Para valorar su afirmación básica, 1 pala debería ser de 52,096 g. Según los manuscritos, se puede deducir que la semilla de mostaza por hora tenía un peso de 3,7 mg. Parece ser que es un valor que no ha cambiado sustancialmente en los años. Sin embargo, la masha no se puede encontrar en ninguna escritura.

La velocidad de caída del agua no tiene una solución analítica sencilla. La altura del agua del vaso de diez palas se reducirá rápidamente a lo largo del tiempo, tal y como se puede observar en la figura (b) superior, vaciándose el recipiente a cero. Al final del tramo, la pendiente de la curva presenta un valor finito, diferente al obtenido en el caso de la clepsida, de forma que el detalle del procedimiento utilizado para la determinación del punto final sufra un incremento considerable. Para que el envase se vacíe en un conflicto, el valor de una masha debe ser de 0,18285 g y el cambio de peso del 0.1% variará el resultado en dieciséis segundos.

Volviendo al caso del reloj de agua Surdava, mediante un sencillo cálculo se puede deducir el valor del equivalente de 1 man:

1 mana = volumen = 1/3\r2h3

donde r = h = 11,4 cm. es. Por lo tanto, 1 mana = 4.654 kg, es decir, equivale aproximadamente a 30 palas. Sin embargo, el propio Al-Biruni ha asegurado que 1 mana y 15 palas son iguales.

(1)VEDANGA JIOTIS (a.C.) 1200-600)(2)PURANA (d.C.? )(3)VISHNU PURANA (h. C. )(4) SURIA SIDANTA (<400 d.C. )(5) Colección de SURIA SIDANTA (<400 dC. )(6) YUANG CHWANG (h. C. 629)(7) AL-BIRUNI (1030 a.C.)

jugaaianasavana divasa	6 años1 año1/2 años(1)	(2)	(3)	(4)	(5)	(6)	(7)
nictemero	día	día	día	día	día	día	día
trimaiatimewatchmuhurt	---48 min	--4 horas 48 min.	----	----	----	12 horas 4 horas 48 minutos	----
nadinadikagatigatikadandadata	-24 min--	------	---24 min-24 min	24 min24 min24 min24 min24-	---24 min-	------	--24 min-
lavapreda	-1min 34s	-	-	-	-	1 min 36 seg.	-
vinadivicalavinadikapalacashak	-----	-----	--24 s24 s	24s----	-24s -	-----	----24 s
prana (respiración)asu	-	-	4s	4s4s	4s	-	4s4s
kastagurvakshara (silaba)tatkshanaaksharanimeshakshanahsuntruti (valor teórico)	1,15 s--0,23 s--= 33 ?s	3,18 s---0,21 s--	-2,4 s-----	------	------	--1,6 s--0,013 skeine	---6min

Relación Ángulo/Tiempo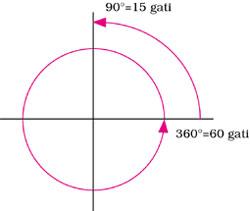 Para llevar a cabo las medidas de tiempo a través de la sombra del cuerpo sobre la superficie es necesario que los astrónomos hindúes conozcan las medidas utilizadas para medir distancias. En general, las sombras se proyectaban sobre superficies esféricas (Kapala Jantra), circulares (reloj de sol o Samrat Jantra), ruedas (Txakra Jantra) o sobre un plano en el que se representaba la línea curva. En todos estos casos, las distancias se medirán en forma de ángulos de circunferencia o semiesfera. Sin embargo, las medidas angulares no coinciden con los grados, minutos y segundos de nuestro sistema sexagesimal. Se utilizó el siguiente criterio: la circunferencia se dividirá en sesenta conflictos, mientras que al gati le corresponden sesenta palas. Finalmente, hay seis pantalones por pala (seis minutos). Así que un prán es un minuto. La circunferencia era la expresión de las bóvedas celestes. Definiendo como unidad de tiempo el intervalo de tiempo que requiere la sombra para llenar un ángulo, sólo se puede relacionar el ángulo formado con el tiempo empleado. Por ello, en muchos casos se utilizó la misma palabra para indicar tanto el ángulo como el tiempo que le correspondía. En la siguiente tabla se resumen los equivalentes. ANGULO TIEMPO NOMBRAMIENTO 1 gati = 6 gradu1 pala = 6 min1 pran = 1 min 24 min24 s4s nadi, nadika, gati, gatika, danda, datavinadi,vicala,vinadika, pala, cashaka,prana, asu Esta definición era muy útil para los astrónomos hindúes porque los planetas no están nunca situados a una distancia superior a 5º o 10º de la eclíptica. Además, podían utilizar las unidades mencionadas para ubicar los planetas. Conociendo las longitudes y latitudes correspondientes a los cuerpos celestes, el planeta podía identificarlos con la ayuda de un goniometro escalonado. Podemos terminar este apartado con una nota importante: ¡cuidado con las unidades al realizar las medidas angulares con los goniometros hindi! !