Le grand temple de Benares

1992/10/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

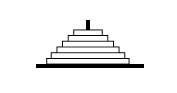
La ville sacrée de Benares se trouve à l'embouchure du fleuve Ganges. Selon la légende, dans le grand temple de Bénares, sous la coupole qui représente le centre du monde, se trouve une semelle d'argent avec trois aiguilles de diamant. Lors de la création, le dieu a mis 64 disques de diamètre différent sur une aiguille, du plus grand situé sur le plateau au plus petit situé à l'extrémité de la pile. La tour de Brahman est ainsi formée. Les prêtres changent les disques d'une aiguille à l'autre constamment jour et nuit, selon les normes fixes et immuables de Brahman, c'est-à-dire que les disques doivent être changés d'un à l'autre et on ne peut pas placer un disque sur un autre plus petit. Le jour où les 64 disques changent de l'aiguille que les dieux ont mise en créant le monde à l'une des deux autres, ce jour-là la tour, le temple et les brahmandarras deviendront poussière et avec un grand dunbots tout le monde disparaîtra.

Cette vieille légende nous pose un problème : calculer le jour où le monde doit disparaître. Pour cela, nous devons trouver le moins de mouvements nécessaires pour effectuer le changement. Cependant, en plus de limiter ce jour, ce problème pose un autre aspect que nous considérons plus intéressant: la méthode de calcul. En fait, la légende du temple de Benares est un bon exemple de recherche. Ce jeu, en plus de son caractère motivant, est un exemple d'un problème qui s'adapte aux différents rythmes d'apprentissage des élèves, pouvant porter des rythmes lents et rapides à la fois.

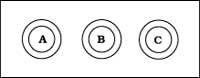
Pas besoin d'aller à Benares pour jouer à ce type de jeux. Sur une tablette, trois coins sont placés et seuls des disques en bois de différentes tailles sont nécessaires, ou sur une feuille, trois cercles sont représentés et des pièces de différentes tailles sont obtenues.

Suggestions didactiques

Pour qu'au début les élèves s'approprient bien le jeu et la norme, ils parleront avec moins de pièces ou de disques. Dans cette première étape, la priorité sera donnée aux normes et non au nombre de mouvements.

La deuxième phase consistera en deux, trois, quatre, cinq disques. Ils comptabiliseront le nombre de mouvements nécessaires pour changer de palette dans chaque cas. Les résultats obtenus par chaque élève seront comparés à ceux obtenus par le reste.

Nombre de disques 123456Nombre minimum de mouvements1371531...Tableau 1.

Dans la troisième phase, on vous indiquera que vous devez effectuer le changement avec le moins de mouvement possible et répéter les exercices de la phase précédente. Ils compareront à nouveau les résultats et les enregistreront dans un tableau.

Dans l'étape suivante, les élèves seront avertis qu'il n'est pas possible d'utiliser la méthode expérimentale pour calculer le moins de mouvements lorsque le nombre de disques augmente. Par exemple, ils peuvent être invités à modifier la tour de sept disques. Compte tenu de la difficulté, les élèves doivent être encouragés à rechercher la formule ou le modèle mathématique qui nous donne le moins de mouvements pour n'importe quel nombre de disques.

Pour cela, ils seront invités à analyser la relation entre les disques et le nombre de mouvements, ainsi que la relation entre le nombre de mouvements. On vérifiera les réponses, propositions, idées, ... Si nécessaire, on leur fera une série de suggestions: différence entre des quantités consécutives, comment obtenir une quantité connaissant la précédente,...

1 = 2 -1

3 = 2 x 2 - 1

7 = 2 x 2 x 2 - 1

15 = 2 x 2 x 2 x 2 -1

31 = 2 x 2 x 2 x 2 x 2 x 2 x 2 - 1

Par:

En suivant cette voie, vous obtiendrez des formules pour les premiers cas avant la fin (tableau 3). De là, nous allons donner la formule générale, complétant dans certains cas les calculs.

Nombre de disques 12345678910Nombre de mouvements 137153163txika2 1 - 12 2 - 12 3 - 12 4 -12 5 - 12 6 - 1

Pour revenir à la légende, le moins de mouvements nécessaires pour changer les 64 disques par aiguilles, selon la formule obtenue, est de 2 64 à 1. Une fois le calcul effectué,

18 3 446.744 2 073.709 1 551.615

Nous obtenons le numéro. Littéralement : dix-huit trillions, quatre cent quarante mille, sept cent quarante-trois milliards, soixante-trois mille, sept cent neuf millions, cinq cent cinquante-cinq mille, six cent quinze (c'est le chiffre de jauges qui apparaît dans la légende des échecs).

En supposant qu'ils ont besoin d'une seconde pour effectuer chaque mouvement, et en agissant constamment, ils auraient besoin de 584.942 1 417.200 ans, environ, pour effectuer tout le changement. Étant donné que la Terre a 3 milliards d'années, nous ne pouvons pas dire que nous sommes en danger.

Sur la base de ce qui précède, nous pouvons inventer d'autres tours qui limitent la durée du monde. Ils suivent les mêmes normes fixes et inaltérables.

Tour de Xiva-Vixun

Les disques de la tour de Brahman sont numérotés de mineur à majeur. Impaires sur l'aiguille gauche

et les paires sont situées sur la droite. Le but est de laisser les paires à gauche et les impaires à droite (commencer avec quelques disques).

Tour d'Allah-Jainko-Kung Ts

Le nombre de disques doit être multiple de trois. Ils sont insérés dans trois aiguilles. L'objectif à cette occasion est de passer les disques de gauche au centre, ceux du centre à droite et ceux de droite à gauche.

Tour des athées

Les disques sont distribués au hasard dans les aiguilles (une, deux ou trois), dans cette distribution les disques

peuvent rester dans n'importe quel ordre. Avec les normes fixes et immuables de toujours, tous les disques doivent être triés sur une aiguille.