El gran templo de Benares

1992/10/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

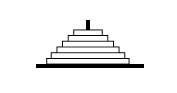
La sagrada ciudad de Benares se encuentra en la desembocadura del río Ganges. Según la leyenda, en el gran templo de Benares, bajo la cúpula que representa el centro del mundo, se encuentra una suela de plata con tres agujas de diamante. En la creación, el dios metió 64 discos de diferente diámetro en una aguja, desde el mayor situado sobre la bandeja hasta el más pequeño situado en la punta de la pila. Se forma así la torre de Brahman. Los sacerdotes cambian los discos de una aguja a otra constantemente día y noche, según las normas fijas e inmutables de Brahman, es decir, los discos deben cambiarse de uno en uno y no se puede colocar un disco sobre otro más pequeño. El día en que los 64 discos cambian de la aguja que los dioses pusieron al crear el mundo a una de las otras dos, ese día la torre, el templo y los brahmandarras se convertirán en polvo y con un gran dunbots todo el mundo desaparecerá.

Esta vieja leyenda nos plantea un problema: calcular el día en que el mundo tiene que desaparecer. Para ello debemos encontrar el menor número de movimientos necesarios para realizar el cambio. Sin embargo, además de limitar este día, este problema plantea otro aspecto que consideramos más interesante: el método de cálculo. De hecho, la leyenda del templo de Benares es un buen ejemplo de investigación. Este juego, además de su carácter motivador, es un ejemplo de un problema que se adapta a los diferentes ritmos de aprendizaje de los alumnos, pudiendo llevar ritmos lentos y rápidos a la vez.

No hace falta ir a Benares para jugar este tipo de juegos. En una tablilla se colocan tres cuñas y sólo se necesitan discos de madera de distinto tamaño, o en una hoja se representan tres círculos y se obtienen monedas de diferente tamaño.

Sugerencias didácticas

Para que al principio los alumnos se apropien bien del juego y de la norma, hablarán con menos monedas o discos. En esta primera etapa se dará prioridad a las normas y no al número de movimientos.

La segunda fase consistirá en dos, tres, cuatro, cinco discos. Contabilizarán el número de movimientos necesarios para cambiar de paletilla en cada caso. A continuación se compararán los resultados obtenidos por cada alumno con los obtenidos por el resto.

Número de discos 123456Mínimo número de movilidad1371531...Tabla 1.

En la tercera fase se les indicará que deben realizar el cambio con el menor movimiento posible y repetirán los ejercicios de la fase anterior. Volverán a comparar los resultados y los guardarán en una tabla.

En el siguiente paso se advertirá a los alumnos de que no es posible utilizar el método experimental para calcular el menor número de movimientos cuando aumenta el número de discos. Por ejemplo, se les puede pedir que modifiquen la torre de siete discos. Dada la dificultad, se debe animar a los alumnos a buscar la fórmula o modelo matemático que nos dé el menor número de movimientos para cualquier número de discos.

Para ello se les pedirá que analicen la relación entre los discos y el número de movimientos, así como la relación entre el número de movimientos. Se comprobarán las respuestas, propuestas, ideas, ... Si fuera necesario, se les hará una serie de sugerencias: diferencia entre cantidades consecutivas, cómo obtener una cantidad conociendo la anterior,...

1 = 2 -1

3 = 2 x 2 - 1

7 = 2 x 2 x 2 - 1

15 = 2 x 2 x 2 x 2 -1

31 = 2 x 2 x 2 x 2 x 2 x 2 - 1

Por:

Siguiendo este camino obtendrán fórmulas para los primeros casos antes de tarde (Tabla 3). De ahí pasaremos a dar la fórmula general, completando en algunos casos los cálculos.

Número de discos 12345678910Número de movimientos 137153163txika2 ¹ - 12 ² - 12 ³ - 12 ⁴ -12 ⁵ - 12 ⁶ - 1

Volviendo a la leyenda, el menor número de movimientos necesario para cambiar los 64 discos por agujas, según la fórmula obtenida, es de 2 ⁶⁴ – 1. Una vez realizado el cálculo,

18 ₃ 446.744 ₂ 073.709 ₁ 551.615

Obtenemos el número. Literalmente: dieciocho trillones, cuatrocientos cuarenta mil, setecientos cuarenta y tres billones, sesenta y tres mil, setecientos nueve millones, quinientos cincuenta y cinco mil, seiscientas quince (ésa es la cifra de galgas que aparece en la leyenda del ajedrez).

Suponiendo que necesitan un segundo para realizar cada movimiento, y actuando constantemente, necesitarían 584.942 ₁ 417.200 años, aproximadamente, para llevar a cabo todo el cambio. Teniendo en cuenta que la Tierra tiene 3.000 millones de años, no podemos decir que estemos en peligro.

En base a lo anterior, podemos inventar otras torres que limiten la duración del mundo. Siguen las mismas normas fijas e inalterables.

Torre de Xiva-Vixun

Los discos de la torre de Brahman se numeran de menor a mayor. Impares en la aguja izquierda

y los pares se sitúan en la derecha. El objetivo es dejar los pares a la izquierda y los impares a la derecha (empezar con pocos discos).

Torre de Allah-Jainko-Kung Ts

El número de discos debe ser múltiple de tres. Se introducen en tres agujas. El objetivo en esta ocasión es pasar los discos de la izquierda al centro, los del centro a la derecha y los de la derecha a la izquierda.

Torre de los ateos

Los discos se distribuyen aleatoriamente en las agujas (una, dos o tres), en esta distribución los discos

pueden quedar en cualquier orden. Con las normas fijas e inmutables de siempre, todos los discos deben estar ordenados en una aguja.