El gran temple de Benares

1992/10/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

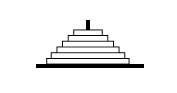
La sagrada ciutat de Benares es troba en la desembocadura del riu Ganges. Segons la llegenda, en el gran temple de Benares, sota la cúpula que representa el centre del món, es troba una sola de plata amb tres agulles de diamant. En la creació, el déu va ficar 64 discos de diferent diàmetre en una agulla, des del major situat sobre la safata fins al més petit situat en la punta de la pila. Es forma així la torre de Brahman. Els sacerdots canvien els discos d'una agulla a una altra constantment dia i nit, segons les normes fixes i immutables de Brahman, és a dir, els discos han de canviar-se d'un en un i no es pot col·locar un disc sobre un altre més petit. El dia en què els 64 discos canvien de l'agulla que els déus van posar en crear el món a una de les altres dues, aquest dia la torre, el temple i els brahmandarras es convertiran en pols i amb un gran dunbots tothom desapareixerà.

Aquesta vella llegenda ens planteja un problema: calcular el dia en què el món ha de desaparèixer. Per a això hem de trobar el menor nombre de moviments necessaris per a realitzar el canvi. No obstant això, a més de limitar aquest dia, aquest problema planteja un altre aspecte que considerem més interessant: el mètode de càlcul. De fet, la llegenda del temple de Benares és un bon exemple de recerca. Aquest joc, a més del seu caràcter motivador, és un exemple d'un problema que s'adapta als diferents ritmes d'aprenentatge dels alumnes, podent portar ritmes lents i ràpids alhora.

No fa falta anar a Benares per a jugar aquest tipus de jocs. En una tablilla es col·loquen tres tascons i només es necessiten discos de fusta de diferent grandària, o en una fulla es representen tres cercles i s'obtenen monedes de diferent grandària.

Suggeriments didàctics

Perquè al principi els alumnes s'apropiïn bé del joc i de la norma, parlaran amb menys monedes o discos. En aquesta primera etapa es donarà prioritat a les normes i no al nombre de moviments.

La segona fase consistirà en dues, tres, quatre, cinc discos. Comptabilitzaran el nombre de moviments necessaris per a canviar d'espatlla en cada cas. A continuació es compararan els resultats obtinguts per cada alumne amb els obtinguts per la resta.

Nombre de discos 123456Mínimo número de movilidad1371531...Taula 1.

En la tercera fase se'ls indicarà que han de realitzar el canvi amb el menor moviment possible i repetiran els exercicis de la fase anterior. Tornaran a comparar els resultats i els guardaran en una taula.

En el següent pas s'advertirà als alumnes que no és possible utilitzar el mètode experimental per a calcular el menor nombre de moviments quan augmenta el nombre de discos. Per exemple, se'ls pot demanar que modifiquin la torre de set discos. Donada la dificultat, s'ha d'animar als alumnes a buscar la fórmula o model matemàtic que ens doni el menor nombre de moviments per a qualsevol nombre de discos.

Per a això se'ls demanarà que analitzin la relació entre els discos i el nombre de moviments, així com la relació entre el nombre de moviments. Es comprovaran les respostes, propostes, idees, ... Si fos necessari, se'ls farà una sèrie de suggeriments: diferència entre quantitats consecutives, com obtenir una quantitat coneixent l'anterior,...

1 = 2 -1

3 = 2 x 2 - 1

7 = 2 x 2 x 2 - 1

15 = 2 x 2 x 2 x 2 -1

31 = 2 x 2 x 2 x 2 x 2 x 2 - 1

Per:

Seguint aquest camí obtindran fórmules per als primers casos abans de tarda (Taula 3). D'aquí passarem a donar la fórmula general, completant en alguns casos els càlculs.

Nombre de discos 12345678910Número de moviments 137153163txika2 1 - 12 2 - 12 3 - 12 4 -12 5 - 12 6 - 1

Tornant a la llegenda, el menor nombre de moviments necessari per a canviar els 64 discos per agulles, segons la fórmula obtinguda, és de 2 64 – 1. Una vegada realitzat el càlcul,

18 3 446.744 2 073.709 1 551.615

Obtenim el número. Literalment: divuit trilions, quatre-cents quaranta mil, set-cents quaranta-tres bilions, seixanta-tres mil, set-cents nou milions, cinc-cents cinquanta-cinc mil, sis-centes quinze (aquesta és la xifra de galgues que apareix en la llegenda dels escacs).

Suposant que necessiten un segon per a realitzar cada moviment, i actuant constantment, necessitarien 584.942 1 417.200 anys, aproximadament, per a dur a terme tot el canvi. Tenint en compte que la Terra té 3.000 milions d'anys, no podem dir que estiguem en perill.

Sobre la base de l'anterior, podem inventar altres torres que limitin la durada del món. Segueixen les mateixes normes fixes i inalterables.

Torre de Xiva-Vixun

Els discos de la torre de Brahman es numeren de menor a major. Imparells en l'agulla esquerra

i els parells se situen en la dreta. L'objectiu és deixar els parells a l'esquerra i els imparells a la dreta (començar amb pocs discos).

Torre d'Allah-Jainko-Kung Ts

El nombre de discos ha de ser múltiple de tres. S'introdueixen en tres agulles. L'objectiu en aquesta ocasió és passar els discos de l'esquerra al centre, els del centre a la dreta i els de la dreta a l'esquerra.

Torre dels ateus

Els discos es distribueixen aleatòriament en les agulles (una, dues o tres), en aquesta distribució els discos

poden quedar en qualsevol ordre. Amb les normes fixes i immutables de sempre, tots els discos han d'estar ordenats en una agulla.