Benaresko tenplu handia

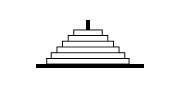
Benares hiri sakratua, Ganges ibaiaren uhertzean dago. Kondairak dioenez, Benaresko tenplu handian, munduaren zentrua adierazten duen kupula azpian, diamantezko hiru orratz dituen zilarrezko azpila dago. Kreazioan jainkoak diametro desberdineko 64 disko sartu zituen orratz batean, azpilaren gainean dagoen handienetik pilaren puntan dagoen txikieneraino. Brahman-en dorrea osatzen da horrela. Sazerdoteek diskoak gau eta egun etengabe aldatzen dituzte orratz batetik bestera, Brahman-en arau finko eta aldaezinen arabera, hau da, diskoak banaka aldatu behar dira eta ezin da disko bat beste txikiago baten gainean jarri. 64 diskoak mundua sortzean jainkoak jarri zituen orratzetik beste bietako batera aldatzen diren egunean, egun horretan, dorrea, tenplua eta brahmandarrak hauts bihurtuko dira eta dunbots handi batez mundu osoa desagertu egingo da.

Kondaira zahar horrek problema bat plazaratu digu; munduak desagertu behar dueneko eguna kalkulatzea, alegia. Horretarako, aldaketa egiteko behar den higidura-kopururik txikiena aurkitu behar dugu. Hala ere, egun hori mugatzeaz gain, problema horrek beste alde bat (gure ustez interesgarriagoa) azaltzen du: kalkulua egiteko metodoa. Izan ere, Benaresko tenpluaren kondaira ikerlana burutzeko adibide egokia bait da. Joko hori, berezko izaera motibatzaileaz gain, ikasleen ikasketa-erritmo desberdinei egokitzen zaien problemaren adibidea da; motelen zein azkarren erritmoak batera eraman bait daitezke.

1. irudia. Brahmanen dorrea.

Ez dago Benaresera joan beharrik horrelako jokoan aritzeko. Oholtxo batean hiru ziri ipini eta neurri desberdineko zurezko diskoak baino ez dira behar; edota, orri batean hiru zirkulu irudikatu eta tamaina desberdineko txanponak lortu.

2. irudia.

Iradokizun didaktikoak

Hasieran ikasleak jokoaz eta arauaz ondo jabe daitezen, txanpon edo disko gutxiagorekin arituko dira. Lehenengo etapa honetan arauei emango zaie lehentasuna eta ez higidura-kopuruari.

Bigarren fasean, bi, hiru, lau, bost, diskorekin arituko dira. Kasu bakoitzean ziriz aldatzeko behar izan duten higidura-kopurua zenbatu beharko dute. Jarraian, ikasle bakoitzak lortu dituen emaitzak beste ikasleenekin alderatuko dira.

Hirugarren fasean aldaketa ahalik eta higidura gutxien erabilita egin behar dutela esango zaie, eta aurreko faseko ariketak errepikatu egingo dituzte. Emaitzak berriro alderatuko dituzte eta taula batean gorde.

Hurrengo urratsean ikasleei honakoa oharteraziko zaie: disko-kopurua handiagotzen denean higidura-kopururik txikiena kalkulatzeko ezin dela metodo esperimentala erabili. Esate baterako, zazpi diskoko dorrea aldatzeko eska dakieke. Zailtasuna ikusita, edozein disko-kopururentzat higidura-kopururik txikiena emango digun formula edo eredu matematikoa bilatzera bultzatu behar dira ikasleak.

Horretarako, diskoen eta higiduren kopuruen arteko erlazioa, baita higidura-kopuruen arteko lotura ere, aztertzeko eskatuko zaie. Emango dituzten erantzunak, proposamenak, ideiak, ... egiaztatuko dira. Beharrezkoa izanez gero, iradokizunak egingo zaizkie: ondoz ondoko kopuruen arteko kendura, nola lortu kopuru bat aurrekoa ezagutuz, 2. taulako berdintzak, ...

1 = 2 -1

3 = 2 x 2 - 1

7 = 2 x 2 x 2 - 1

15 = 2 x 2 x 2 x 2 -1

31 = 2 x 2 x 2 x 2 x 2 - 1

........................................

Bide horri jarraituz berandu baino lehen lehenengo kasuetarako formulak lortuko dituzte (3. taula). Hortik formula orokorra ematera pasako gara, zenbait kasutan kalkuluak burutuz.

Kondairara itzuliz, 64 diskoak orratzez aldatzeko behar den higidura-kopururik txikiena, lortutako formularen arabera, 2 ⁶⁴ – 1 da. Kalkulua egin eta gero,

18 ₃ 446.744 ₂ 073.709 ₁ 551.615

zenbakia lortzen dugu. Hitzez esanda: hamazortzi trilioi, laurehun eta berrogeitasei mila, zazpiehun eta berrogeitalau bilioi, hirurogeitamahiru mila, zazpiehun eta bederatzi milioi, bostehun eta berrogeitamaika mila, seiehun eta hamabost (hori da, hain zuzen, xakeko kondairan agertzen den galgarau-kopurua).

Higidura bakoitza egiteko segundo bat behar dutela pentsatuz, eta etengabe ihardunez gero, aldaketa osoa burutzeko 584.942 ₁ 417.200 urte, gutxi gorabehera, beharko lituzkete. Lurrak 3.000 milioi urte dituela kontutan hartuz, ezin dugu esan arriskuan gaudenik.

Aurrekoan oinarrituz, munduaren iraupena mugatzeko beste dorre batzuk asma ditzakegu. Arau finko eta aldaezin berberek diraute.

Xiva-Vixnu-ren dorrea

Brahmanen dorreko diskoak zenbakitu egiten dira, txikienetik handienera. Bakoitiak ezkerreko orratzean

3. irudia. Xiva-Vixnu-ren dorrea.

eta bikoitiak eskuinekoan kokatzen dira. Helburua bikoitiak ezkerrean eta bakoitiak eskuinean uztea da (hasi disko gutxirekin).

Allah-Jainko-Kung Tse-ren dorrea

4. irudia. Allah-Jainko-Kung Tse-ren dorrea.

Disko-kopuruak hiruaren anizkoitza behar du izan. Hiru orratzetan sartzen dira. Helburua, oraingoan, ezkerreko diskoak erdira, erdikoak eskuinera eta eskuinekoak ezkerrera pasatzea da.

Ateoen dorrea

Diskoak zoriz banatzen dira orratzetan (batean, bitan edo hiruretan), banaketa horretan diskoak

5. irudia. Ateoen dorrea.

edozein ordenatan gera daitezkeelarik. Betiko arau finko eta aldaezinak erabiliz, disko guztiak orratz batean kokatu behar dira ordenaturik.