Història de l'Abaco

Com comentem a l'inici de la història de les xifres, abans que apareguessin l'alfabet i les xifres, els éssers humans utilitzaven principalment dos sistemes de comptabilització, el de les osques i els cants. El que ens interessa ara és el dels cants, ja que és l'origen dels àbacs.
En alguns pobles, per a comptabilitzar als soldats o a les ovelles, els cants es dipositaven en rases excavades en el sòl; s'apilaven deu cants i se substituïen per una altra pedra major, és a dir, s'utilitzava la base deu. Cada rasa representava una remodelació de deu. En altres pobles, les rases eren substituïdes per plaques de ferro o estrabos de fusta i les bitlles perforades per a poder moure's per les planxes o estreps. Així van néixer els marcadors de boles.
Amb la paraula Abako indiquem tres calculadores diferents. El primer, utilitzat per moltes cultures antigues, era el tauler trencat o la pròpia terra. Les xifres o símbols geomètrics podien escriure's amb un dit o amb un tascó. En general, la paraula grega abax significa taula plana o taula sense potes. El seu origen podria ser la paraula hebraica abaq, el significat de la qual és pols. Els hindús van utilitzar aquest tipus d'àbacs VI. Fins al segle XX per a realitzar càlculs amb les seves xifres.

El segon tipus de calculadora és el de taules. En aquestes taules es dibuixaven línies paral·leles que indicaven un ordre numèric. Per a realitzar els números i càlculs es col·locaven damunt unes corregudes o fitxes. A aquestes peces els grecs deien els psehones i els romans calculi. Aquestes línies podien ser traçades sobre pergamas, tallades en marbre, tallades en fusta o brodades en teles.
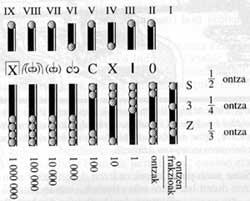
En els àbacs de Roma, cada columna (o fila) representava una recomposició de deu; de dreta a esquerra i començant per les unitats. A vegades la columna estava dividida en dues parts. En la part inferior una fitxa indicava una unitat de l'ordre corresponent. En la part superior, no obstant això, una fitxa valia la meitat d'una unitat de l'ordre següent (o cinc unitats de l'ordre corresponent). Això és en la primera columna 5, en la segona 50, etc.
En un baix relleu d'un sarcòfag romà del segle I, un jove calculator, amb comptes a les cases dels majoristes, pot veure's davant el seu mestre amb una calculadora mòbil d'aquestes característiques.
El mòbil d'Abako era una tauleta metàl·lica amb ranures paral·leles. A través de les escletxes es movien els botons de grandària adequada. Cada escletxa corresponia a un ordre decimal, a excepció dels dos primers de la dreta. Aquests s'utilitzaven per a la dotzena o criança de l'AS i per a la meitat, terç i quart de la vaixella. Així, la tercera ranura dreta a les unitats, la quarta a les deu, etc. corresponents. A més, cadascuna de les ranures (excepte la primera) estava dividida en dues parts, amb quatre botons en les inferiors i un botó en les superiors. Els botons de baix valien una unitat d'ordre i els de dalt cinc. Aquesta calculadora mòbil s'assembla molt als marcadors de boles utilitzats en Països d'Extrem Orient i Pròxim Orient.
Des de la destrucció de l'Imperi romà fins al final de l'Edat mitjana, a l'Europa occidental va estar en mans d'unes poques ciències. Aquests, una vegada apresos a llegir i a escriure, abordaven temes com l'Astronomia, la Geometria o el Càlcul. El càlcul el feien amb els dits i escrivien la xifra en romà. Cal dir que només els especialistes sabien realitzar operacions aritmètiques i les realitzaven mitjançant àbacs romans. En l'actualitat, l'especialista de l'època necessitava moltes hores per a realitzar l'operació que un nen podia realitzar en pocs minuts. Quan les coses estaven així, els que volien prendre consciència del càlcul es dirigien cap a Itàlia, que llavors tenia un major contacte amb àrabs i byzanzios, i les seves classes eren especialitzades en operacions complexes.
L'any 999 va ser nomenat Papa Gerbert d’Aurillac. Anteriorment havia estudiat els mètodes àrabs i va intentar penetrar per Europa, però va trobar una gran resistència. Al principi, els símbols àrabs (hindús) introduïts per Gerbert van ser escrits en fitxes d'os de branca i van substituir als cants en les columnes de l'àbac. No obstant això, els calculadors retrògrads van preferir imprimir xifres romanes.
Entre els anys 1095 i 1270 destaca la de Croada. Si el seu objectiu era destruir les idees dels infidels, van obtenir altres resultats. Una d'elles va ser la presa de consciència de la cultura que alguns cavallers i clergues presents volien eliminar. Quant al càlcul, van conèixer el zero i les tècniques hindús de càlcul.
A més, a l'altre costat del Mediterrani, en la Península Ibèrica, concretament a Toledo, es van intensificar els contactes entre tots dos mons. Des de finals del segle XX. Aquests dos fets van donar lloc a la mort de l'àbac.

La mort es va accelerar en el segle XIII. A principis del segle XX, el matemàtic Leonardo Fibonacci de Pisa, autor del llibre "Àbac Abaci". Aquest tractat no va afectar, com es podia imaginar, a l'aritmètica de l'àbac, sinó a les regles del càlcul de xifra sobre la sorra. Per això es va convertir en manual de suport a l'algorisme. En conseqüència, la ciència dels càlculs mitjançant xifres (l'aritmètica) es va estendre al poble pla. La senzillesa d'aquest càlcul va fer que la pròpia Església qüestionés si la nova aritmètica no tenia una cosa màgica o demónico. D'aquí a cremar en el foc a uns fogosos partidaris de Fibonacci només hi havia un pas, donat per alguns inquisidors.
La veritat és que la disputa entre els abaquistas i els algorítmics es va estendre durant segles i després de guanyar nous mètodes s'utilitzava l'àbac. XVIII. En el segle XVIII els càlculs en ploma es verificaven mitjançant àbac. Mentre els nous càlculs van ser conquistats pel científic, comerciants, banquers, funcionaris, etc. van continuar utilitzant l'àbac.

La revolució francesa va acabar decidint la qüestió. En aquella època es va prohibir l'ús escolar de l'àbac.
El tercer tipus d'àbac és el dels marcadors de bola. Els marcadors s'utilitzen principalment en Països de l'Est: En la Unió Soviètica, la Xina, el Japó, Singapur, Corea, Taiwan, etc. En elles veurem tres tipus diferents: Tipus de stchoty en el foc xinès, pa, sorobe japonès i stchoty rus.
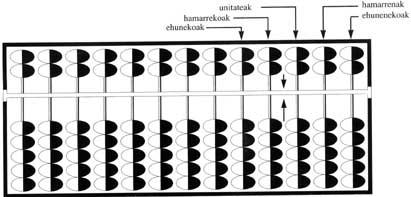
En el foc de la Xina l'origen de la pana és desconegut, però sabem que el XVI. En el segle XX ja s'utilitzava. En el foc (calcular) en l'ideograma xinès es veu un àbac, un ideograma en el qual la mà representa sota i damunt el bambú. En el foc la pana està formada per quatre llistons o estreps que formen un rectangle, diversos pals de bambú (8-15) units als estreps llargs, un altre estrabe que separa aquests pals en dues parts (part superior i inferior) i dues en la part superior i cinc en la inferior, i set boles mòbils de dalt a baix. Per descomptat, quants més bastons tinguem, major serà el número que es podrà indicar.
En general, els dos pals de la dreta (columnes) es deixen per als de la dècima i la centèsima, quedant les unitats en la tercera. Les boles de la part inferior valen una unitat de l'ordre corresponent, mentre que les de la part superior valen cinc. Les boles superiors i inferiors per a representar els números s'emporten a l'estrabe intermedi.
Sense els seus llavis, l'anomenat Soroban del Japó va ser traslladat des de la Xina, en el segle XVI. En el segle XX, apika. XIX. Va conservar el seu aspecte original fins a mitjan segle XX. Després es va anar perdent una bola superior i II. Des de la Guerra Mundial van perdre la cinquena bola de la part inferior que sobrava. Al Japó encara se celebren competicions de càlcul per àbac o camp. En el seu moment va ser molt popular una competició de càlcul celebrada en 1945. En ella Kiyoshi Matsuzaki, campió japonès de camp, es va imposar en quatre de cada cinc proves a Thomas Nathan Woods, l'operador més expert en calculadores electròniques de l'exèrcit estatunidenc al Japó.
Els soviètics van conèixer la stchotya a través dels àrabs. Prova d'això és la seva utilització en algunes regions de l'Índia i Orient Pròxim. Els turcs criden choreb a les coulbas i armènies.

L'stchoty de la Unió Soviètica no és igual als anteriors. No hi ha estreps intermedis. Cada pal té deu boles, les dues centrals (5 i 6) de diferents colors. En alguns stchotys, en alguns bastons només es col·loquen quatre boles per a les fraccions de ruble i copecas. En l'stchoty, les boles de números han d'anar a l'estrabe superior.
Aquests tres marcadors de boles són actualment utilitzats per molta gent als seus pobles, però sobretot per comerciants i comerciants.
Finalment, assenyalar que en els últims anys s'ha reconegut la utilitat de l'ensenyament de l'aritmètica als nens cecs i que a les escoles també s'estan obtenint bons resultats en didàctica de les matemàtiques.
Fins ara hem parlat de la història de l'abaco, però perquè no sigui història i per a recuperar-la de la història, en el pròxim número et donarem la normativa d'ús de l'abaco xinès. Per a això li recomanem que, si és possible, disposi d'un àbac xinès. Per descomptat, en un primer moment t'embussos els dits, et mous les boles, t'equivocaràs en els càlculs, però et resoldràs amb experiència i paciència.

Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian