Ulertzeko errazak baina ebazteko zailak diren matematikako problemak

Ingeniaritzan, biologian eta beste hainbat arlotan aplikatzen diren problemak ikertzen dituzte matematikariek. Izan ere, matematiketan oinarritutako frogapenei esker, munduan eta naturan gertatzen diren fenomenoen portaera ulertzeko aukera dugu.

Batzuetan, matematikan aztertzen diren problemak ekuazio erraldoiz osatuta daude, eta, hori dela medio, jende askok uste du oso zailak direla ebazten. Beste problema batzuk, berriz, oso errazak dira ulertzeko (kasu askotan, lerro batean azaldu daitezke), baina matematikariek urteak eman dituzte haien frogapena bilatzen. Hortaz, ebazteko oso zailak direla esan dezakegu. Artikulu honetan, erraz azaldu daitezkeen (baita ulertu ere) baina frogatzeko zailak diren problema matematikoen inguruan hitz egingo dugu.

Utzidazue azaltzen zer den problema matematiko bat ebaztea. Demagun X deituriko problema ebatzi nahi dugula. Nola egiten da hori? X gezurra dela frogatzeko, nahikoa da adibide aurkitzea. Esate baterako, har dezagun problema hau: ''zenbaki guztiak arruntak dira''. Hori gezurra dela frogatzeko, arrunta ez den zenbaki bat eman behar da, adibidez, 3/2. Horrekin ondoriozta dezakegu zenbaki guztiak ez direla arruntak. Baina, X egia dela ondorioztatzeko, frogapen bat behar dugu. Jo dezagun problema hau: ''hiruz zatitu daitezkeen zenbaki guztien zifren batura hiruz zatitu daiteke''. Adibidez, 12 zenbakia hiruz zatitu daiteke; haren zifren batura 1 + 2 = 3 da, eta hiruz zatitu daiteke. Beste adibide bat 273 da, 2 + 7 + 3 = 12 baita. Gure asmoa da, ordea, zenbaki guztiek propietate hori betetzen dutela ondorioztatzea. Beraz, ez da nahikoa bi adibide horientzat egia dela egiaztatzea, eta matematikan oinarritutako arrazonamendu bat aurkitu behar da. Hori lortuz gero, frogatuko da problema edozein zenbakitarako egia dela (eta inork ezingo du esan gezurra denik).

Andrew Wiles-ek frogatu zuen Fermaten azken teorema 1994an. Arg. Klaus Barner_CC-BY-SA 3.0

Fermaten azken teorema 1640. urte inguruan proposatu zen. Oso erraz azaltzen den problema da; Fermatek liburu baten izkinan idatzi zuen.

''Izan bedi n > 2 den zenbaki arrunt bat. Ez dago hurrengo berdintasun hau beteko duen a, b eta c zenbaki arruntik: aⁿ + bⁿ = cⁿ .''

Matematikari asko saiatu ziren problema hori frogatzen, baina ez zuten lortu harik eta 300 urte baino gehiago pasatu arte. Andrew Wiles matematikariak frogatu zuen, 1994. urtean, Fermaten azken teorema, eta esaten dute horretarako zortzi urte eman zituela lanean.

Problema matematiko famatu bilakatu da Fermaten azken teorema, matematikaren munduan ez ezik, liburu, film eta beste hainbat lekutan ere aipatzen baita. Baina Fermaten azken teoremaz gain, badira beste problema asko azaltzeko errazak baina ebazteko zailak direnak. Hona hemen halako problema ezagunenak:

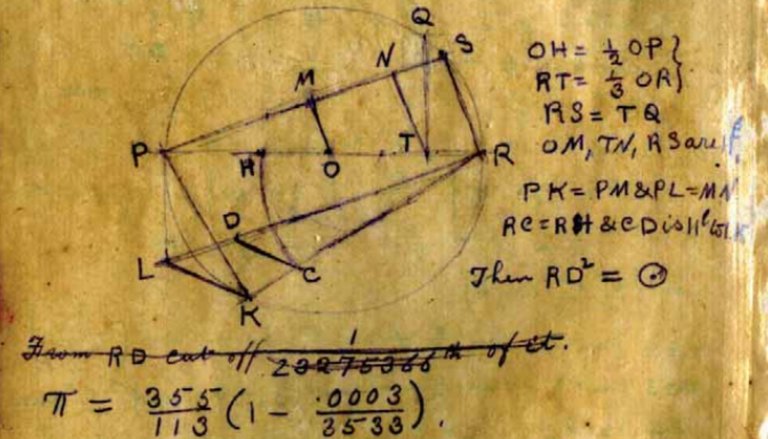
1. Zirkuluaren koadratura

Zirkuluaren koadraturaren problema honela aurkez daiteke:

Zirkuluaren koadraturaren ebazpena Ferdinand von Lindemannek eman zuen, 1882an.

''Izan bedi R erradioko zirkulua. Erregela bat eta konpas bat bakarrik erabiliz, marraztu zirkuluaren azalera bereko lauki bat.''

Babiloniarrek bazituzten problema honen hurbilketak K.a. 500. urtean, jadanik. Baina problemaren ebazpena Ferdinand von Lindemannek aurkeztu zuen askoz geroago, 1882. urtean. Matematikari horrek π zenbakia transzendente dela frogatu zuen, eta emaitza hori erabiliz ondoriozta daiteke zirkuluaren koadraturaren problema ezin dela egin.

2. Zenbaki lehen bikien problema

Zenbaki lehenak bat zenbakiaz (1) eta bere buruaz bakarrik zatitu daitezke. Esate baterako, 7 zenbaki lehena da. Zenbaki lehenak mugagabeak dira, hau da, infinitu zenbaki lehen daude. Emaitza hori Euklidesek frogatu zuen, K.a. 300. urtean, eta Elementuak liburuan idatzi zuen.

Esaten dugu bi zenbaki a eta b zenbaki lehen bikiak direla, baldin eta haien arteko distantzia bi bada, alegia, a = b + 2 edo b = a + 2 bada. Adibidez, 5 eta 7 zenbaki lehen bikiak dira. 11 eta 13 ere bai. Zenbaki lehen bikien problemak zera dio:

''Zenbaki lehen bikien kopurua infinitua da.''

Gaur egun, problema matematiko irekia da hau, alegia, matematikariek ez dute frogatzea lortu. Eta aurkitu diren zenbaki lehen bikirik handienak 3756801695685 · 2⁶⁶⁶⁶⁶⁹ ± 1 dira. Beraz, zenbaki lehen bikiak mugagabeak direla uste da, eta, norbaitek egia ala gezurra den frogatu arte, aieru izaten jarraituko du.

Preda Mihăilescuk Catalanen aierua frogatu zuen 2002an. Arg. Volker Krummel

3. Catalanen aierua

Lehenik eta behin, argi gera bedi problema honek ez duela zerikusirik Kataluniako biztanleekin. Eugène Charles Catalan matematikariak 1884. urtean proposatuko problemak honela esaten du:

''Bikote bakarra dago kontsekutiboa eta zenbaki arrunten berredura dena: 2³ eta 3².''

2³ eta 3² zenbaki arrunten berredurak eta kontsekutiboak dira, haien emaitzak zortzi eta bederatzi direlako, hurrenez hurren. Horretaz gain, aieruak esaten du ez dagoela inolako x, y, p eta q zenbaki arruntik berdintza hau betetzen duenik: x^p – y^q = 1. Problema hau erraz azaldu arren, oso zaila izan zen matematikarientzat frogatzea, eta, azkenean, Preda Mihăilescu matematikariak frogatu zuen, 2002. urtean.

4. Goldbachen aierua

Goldbachek Eulerri 1742an bidalitako gutun honetan proposatu zuen bere aierua.

Goldbachen aieruak honela dio:

''Bi baino handiagoa den edozein zenbaki bikoiti bi zenbaki lehenen batura da.''

Hona hemen adibide bat: 10 = 3 + 7, non 3 eta 7 zenbaki lehenak diren. Beste adibide ezagun batzuk dira 20 = 13 + 7 eta 30 = 13 + 17. Zenbaki horiek, beraz, propietate hori betetzen dutela ikusi dugu. Baina edozein zenbaki bikoititarako hori egia dela esateko, frogapen bat behar da.

Goldbachek Eulerri 1742. urtean zuzendutako gutun batean agertu zen problema hau lehenengo aldiz. Orduz geroztik, matematikari asko aritu dira problema horretan lan egiten. Azken urteotan, zenbakizko metodo oso konplexuak garatu dira problema aztertzeko, eta, analisi horien arabera, 10¹⁸ baino txikiago diren zenbaki guztiek betetzen dute Goldbachen aierua. Hori dela eta, ebazpen hori egia dela uste dute matematikari gehienek, baina oraindik ez dute frogapenik aurkitu.

Azaltzeko errazak baina ebazteko oso zailak diren problemak ikusi ditugu, eta, horrelako problema asko dauden arren, artikulu honetan, adibide batzuk besterik ez idaztea pentsatu dut. Bestalde, azaltzeko zailak eta ebazteko errazak diren problema matematikoak ezagutzen ditut, baina horiek, zuen baimenarekin, beste une batean ikusiko ditugu.

Erreferentziak

''Zenbaki lehen bikiak''. Elhuyar aldizkaria. 2008/08/01.
''Fermaten azken teoremaren inguruan.'' Elhuyar aldizkaria. 1995/05/01. Idazlea : Javier Duoandikoetxea Zuazo.
''John Harper, matematika eta ahateak ikertzen''. Zientzia Kaiera. 2015/11/15. Idazlea : Josu Doncel Vicente.
''Modular elliptic curves and Fermat's Last Theorem''. Annals of Mathematics 142 (2). Idazlea : Andrew Willes.
''Uever die Zahl pi''. Mathematische Annalen 20 (2). Idazlea : Ferdinand von Lindemann.