Limit of black holes in the surrounding area (and II)

1993/05/01 Arregi Bengoa, Jesus Iturria: Elhuyar aldizkaria

• Astrofisika

Logically, the structure of the black holes that are turning (black holes of Ker) is more complex than that of those that have no turns, so the phenomena that can occur around the border are also more unique. On this occasion we present a curious idea based on this peculiar structure, a conjecture that introduces us almost in the field of science fiction: the process of subtraction of energy to the black hole.

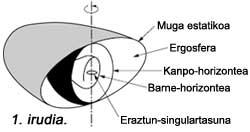
We begin, however, by clarifying the structure of Ker's black holes and later explaining this process. Figure 1 will help us in this work. As can be seen, in the case of the black hole with twist, we do not find the singular point of infinite density in the middle of black static holes (black holes of Scharzschill). The singularity is now a ring located in the equatorial plane. This ring, moreover, is not the inevitable destiny of matter that falls into the black hole. It is possible to walk through the black hole without falling to the singularity, excelling outside the plane in which it is located or passing through the ring.

As for the limit of the black hole, what we did in the case of the static black hole with a single limit called “event horizon”, we will now explain it through three surfaces. The surface we have drawn in Figure 1 with the name of “outer horizon” is the true limit of the rotating black hole, that is, if we fall inside it, it cannot be exited. The inner horizon is the limit of any signal emitted by the singularity of the ring, since its outer propagation is not possible. What is, therefore, the peculiarity of the static limit? In Schwarzschill's black hole, the limit of events was not only the limit of the black hole, but also the limit of the time exposed in the previous number being "frozen."

In the black hole of Ker this last phenomenon occurs in the static limit. As we will see later, this distinction between the outer horizon and the static limit is what allows us to steal energy from the black hole. The space between the two surfaces mentioned is called ergosphere. But to understand how energy can be extracted, we must make some observations on the dynamics of black holes.

As is known, to fully describe the black hole are sufficient three data: mass, angular momentum and load. One type of energy corresponds to each of these magnitudes: the first one, the corresponding to the inert mass, the second one, the turning energy corresponding to the angular moment and finally, the electric energy corresponding to the load. On the other hand, the dynamic state of the black hole can be expressed by two parameters: the surface of the black hole (the surface of the event horizon) and the surface gravity, that is, the value of the acceleration of gravity over the event horizon. If the black hole suffers any variation, for example by ingestion of more matter, its new mass and angular momentum can be calculated under the function of the two quantities cited.

Specifically, the surface of the black hole is closely linked to its mass. Any transformation, by not being able to extract the material from the black hole, can never reduce the surface of the black hole. Therefore, the energy associated with the mass cannot leave the black hole in any case, but D. Christodolou showed that the other two types of energy are removable. From this point of view, from the Schwarzshild hole, that is, without turning or loading, no energy can be extracted, but it can be from the rotating black hole or with load. Process theories have been invented to remove both types of energy. On this occasion R. We will explain what designed by Penrose.

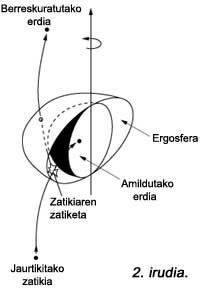
Basically, the process is the one shown in Figure 2. Think that we have launched a rocket into the black hole and when it enters the ergosphere it is divided in half. If one of the fragments crumbles into the black hole following a retrograde orbit, an orbit against the direction of turning of the black hole, when entering the black hole its angular moment decreases. The other part can return from the ergosphere, with more energy than the initial rocket had.

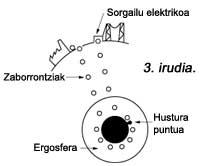
C. C. Mizner, K. Thorne and J. Wheeler could get R. They proposed a way of taking advantage of Penrose's idea. The master lines of this path are illustrated in figure 3. The platform that can be seen in it is quite far from the black hole so that it is not affected by the tidal forces. It is considered that on the platform there is an industrial estate with the desired width. All the waste and waste generated would be collected in containers and thrown into the black hole from an appropriate place.

Once the container enters the ergosphere it would open and the garbage would be deposited in one of the retrograde orbits mentioned above, and subsequently removed from the ergosphere, recovering in a suitable “port” of the platform. A generator affected by the kinetic energy of the containers would result in a strong supply of the polygon. Therefore, all the garbage would be destroyed without any harmful effect and in return its energy equivalent and another amount stolen from the black hole would be collected. The proposal is unsustainable.

ANNIVERSARIES SUN: May 21 enters Gemini 1h 1min (UT). MOON: FULL MOON FOURTH WANING NEW MOON GROWING ROOM Now (UT) 63 h 34 min 1312 h 20 min 2114 h 6 min 2818h 21min PLANETS MERCURY: This month is very difficult to see because day 16 is in superior conjunction. VENUS: We can see it in the morning in better conditions, but we still have little time before we begin to cover the lights of dawn. MARTITZ: it is visible in the sky nothing more darkening. It disappears in the vicinity of 1h 30min (UT) at the beginning of the month and at the end of the month for 0h (UT). JUPITER: We can see it through the sky all night. However, by the end of the month it begins to hide before dawn. SATURN: leaves in the second half of the night. Initially about 3h (UT), but before 1h (UT) for the end.