Historia de las cifras (V)

1990/09/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Despliegue del nuevo sistema

El sistema hindú tardó mil años en llegar hasta Europa, donde los árabes fueron mediadores.

La expansión árabe (VIII-XIII. Durante el siglo XIX, todos los pueblos reunieron obras griegas, filosóficas, científicas o literarias y las arabicaron. En todos los lugares se crearon bibliotecas y universidades. Bagdad, Damas y más tarde las ciudades de Alkairo, Kairuan, Fez, Granada y Córdoba se convirtieron inmediatamente en centros científicos.

En Europa XI. Hasta el siglo XX se vivió una crisis política y científica. Por ejemplo, para enseñar aritmética teórica, el Nicomaco de Geresa (d.C.) II. siglo XX), inspirado por una obra matemática floja del griego Boecio (d.C.) En el siglo V se utilizaba una obra que se atribuía al latino. En cuanto a la aritmética práctica, manejaban la numeración romana y el ábaco.

Los árabes, al principio, asimilaron la numeración alfabética griega y hebrana y la adaptaron al alfabeto de sus 28 letras. Por otro lado, se recuperó el sistema de posición sexagesimal y el cero de los babilonios. Pero cuando conocieron el sistema hindú a través de las relaciones comerciales, lo hicieron en su totalidad.

Los árabes no se quedaron en ello y aportaron a la cultura. A la hora de recopilar y traducir los trabajos antiguos se hicieron algunos comentarios. Además, la rigidez de sistematización de los matemáticos griegos se asoció a la practicidad de la ciencia hindú.

Entre los matemáticos árabe-islámicos destaca el samanés Mohamed Ibn Mussa al-Khowarizmi (780-850). Es conocido por sus dos libros. En la primera se habla de aritmética y en ella se explica el sistema hindú con ejemplos. Posteriormente se abriría con éxito en la Europa occidental. De hecho, el nombre latino del autor se convirtió en el sinónimo del sistema. En su segundo trabajo trató la ciencia algebraica. También fue famoso. El título de este trabajo comenzaba con la palabra alj. Una de las dos operaciones que cambiaban de sección los términos para dejar términos positivos en dos partes de una ecuación se llama:

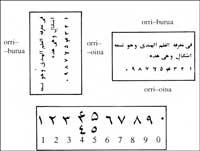
Cuando los árabes conquistaron el sistema hindú, no hicieron más que copiar las cifras. Después de pasar por las manos de los copistas cambiaron de aspecto.

Un motivo de cambio aparente se encuentra en la escritura, ya que escribían por columnas, de izquierda a derecha. Le daban un giro de 90° para leer, en el sentido de las agujas del reloj. Sin embargo, fueron cifras que se difundieron por las provincias árabes y que ellos llamaban “hindi”.

Pero nuestras cifras no proceden directamente de éstas, sino de las de los árabes occidentales. IX. En el siglo XVIII se rompió el imperio árabe-musulmán, quedando fuera del califato de Bagdad el África noroccidental y la región musulmana de la Península Ibérica. Sin embargo, las relaciones no se rompieron, sobre todo por peregrinaciones hasta La Meca, intercambios comerciales, guerras y migraciones de población. Los árabes orientales enseñaron a los occidentales el sistema hindú. En esta región las cifras evolucionaron de manera diferente.

Estas cifras se denominaban “ghobares” (cifras en polvo) por el polvo que se esparcía para poder escribir las cifras en las tablas de cálculo. Este cambio aparente se debe a la forma gráfica de los copistas occidentales.

Mientras los árabes conocieron el sistema hindú, tuvieron que pasar siglos para que los europeos lo aceptasen. En la Europa de la época, desde la abolición del Imperio romano hasta el final de la Edad Media, el cálculo (cálculo por ábaco) estaba en manos de privilegiados. Sin embargo, los occidentales podían obtener las ventajas del sistema hindú gracias al monje Gerbet d’Aurillac, que en el año 999 fue nombrado Papa Silbestre II. En el convento Gerbert había estudiado matemáticas y astronomía. Durante su estancia en la Península Ibérica estudió el sistema de numeración y métodos de cálculo de los árabes. Como director de la escuela diocesana de Reims intentó aplicar sus estudios. Pero, desgraciadamente, sólo logró introducir cifras (salvo cero). En los ábacos de columna se sustituyeron los cantos por cifras, pero en aquellos ábacos no era necesario el cero.

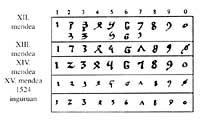
Al igual que ocurrió con los árabes, en Europa las cifras se distorsionaron por diferentes motivos; por escribir de fantasía, por copiarlas boca abajo o indirectamente, etc.

Tras el paso de las cruces se recuperaron las grafías originales. XIII. y XIV. A partir de los siglos XVI se convirtió en la imagen actual. La imprenta de Gutenberg fijó para siempre las formas de las cifras. Si bien el objetivo de las cruzadas no era la reconquista de la ciencia y la cultura, fue uno de los resultados. Los cruzados que se dirigieron a Tierra Santa regresaron con la cultura local. Los cruzados tuvieron intercambios comerciales y culturales con los musulmanes. Gracias a ellos el sistema hindú se adentró en Europa.

Al otro lado del mar Mediterráneo, en la Península Ibérica, XI. Desde finales del siglo XX los intercambios culturales se fortalecieron gracias a las obras de los traductores. Entonces los cristianos empezaron a traducir todos los trabajos al latín.

En ese ambiente destacó un matemático italiano: Leonardo de Pisa, llamado “Fibonacci”. Estudió el sistema árabe en África musulmana y Oriente Próximo. Posteriormente, en el año 1202, presentó el trabajo Liber Abaci (Tratado de Abaco), en el que explicaba las reglas del cálculo de cifras. A partir de ahora los aficionados al nuevo cálculo se multiplicaron. Sin embargo, el desarrollo estaba lejos.

Había dos razones principales para que no se aprobara el nuevo cálculo. Por un lado, los “dueños” del antiguo cálculo veían peligrar su vida. Por otra parte, existía la Iglesia, que pidió que el desarrollo de la ciencia dependera de sus dogmas. La facilidad de cálculo de los árabes fue acusada a Satanás.

También nos ayudará la etimología de cero y cifras. La palabra cero proviene de la palabra sanscrítica sifr (hutsa, hinduen sunya). Fibonacci, que en su obra Liber Abaci le llamó zephirum, más tarde se convirtió en cefiro y a partir de 1491 quedó cero. Pero de la palabra sifr también viene la palabra cifra. Sus transcripciones en latín Sifra, Cifra, Cyfra, Tzyphra, Cifre, Cyfre, etc. son. En un principio esta palabra tuvo el significado de cero. Para entenderlo hay que volver al ambiente que marca la Iglesia. El uso de cifras árabes estuvo prohibido en su día. Por otro lado, la gente utilizaba el sistema oculto y empezó a denominarse “cifra”, mezclando ambos significados (cero y cifra). Los expertos trataron de mantener su significado original, pero no lo consiguieron.

Los científicos se mostraron inmediatamente a favor del nuevo sistema. A los comerciantes, banqueros, funcionarios y en general atrasados les costó mucho abandonar el ábaco. Situación durante la Edad Media y el Renacimiento XVII. y XVIII. Se mantuvo en las administraciones hasta los siglos 20.

¿Se acabó?

Finalmente y tras una larga historia de obstáculos, nuestro sistema se completó. ¿Pero ha terminado la historia de las cifras? Al menos así lo creemos. A pesar de cambiar la grafía de las cifras cuando aparecen los ordenadores, su nombre no se ha movido. Podríamos pensar en otras bases como las 12 o 2 (las de los ordenadores). Sin embargo, el sistema no cambiaría. Subsistirían el principio de posición, el cero y las reglas de cálculo.

Desde la época del hombre Crô-Magnon hasta el hombre moderno no ha habido cambios básicos en el cerebro, sino riqueza cultural. El matemático Leopoldo Kronecker dijo: “Dios creó el número natural, el resto obra humana”. O en palabras del filósofo alemán Lichtenberg: “El hombre empezó desde el principio: toda magnitud es igual a sí mismo, y llegó a medir el Sol y las estrellas”.

La teoría de la visita de seres de otros mundos ha fallado en este campo. Si eran tan rápidos, ¿por qué no nos dejaron la numeración de posición y el cero?

En cifras no hay torre de Babel. Mientras en todo el mundo hay más de cuatro mil lenguas y decenas de alfabetos, en la actualidad todos los pueblos han aceptado el sistema de cifras hindú.

Este sistema ha permitido la creación y desarrollo de calculadoras y tratamiento de la información. Esto no hubiera sido posible con otros sistemas. Al principio Leonardo de Vinci, Pascal, Leibniz, Babbage,... (mecánica) más tarde Hallerith, Torres Quevedo, Arken,... (electromecánica) y finalmente Turing, Atanasoff, Von Neumann,... Esto se debe a la labor realizada por los científicos (electrónica).

Junto a las cifras se desarrolló el concepto numérico y la escritura matemática.

Durante mucho tiempo no se podían escribir números negativos, ni tampoco remisiones como 4 - 7. El concepto cero dio esa oportunidad.

Otro logro ha sido definir y unir conceptos diferentes. Por ejemplo, las fracciones. Se conocen desde la antigüedad. Los egypti sólo conocían las fracciones originales (cuando el numerador es 1). Los babilonios dieron a las fracciones una redacción racional, creando fracciones sexagesimales. Los griegos, ante la imposibilidad de su numeración alfabética, adoptaron el sistema babilónico. La escritura moderna se debe a los hindúes y la invención de la línea a los árabes.

Posteriormente, el descubrimiento de las fracciones decimales (cuando el divisor es la reversión decimal) permitió escribir cifras a la derecha de la coma. En Europa, el primero fue el belga Simón Stevin, que escribió en 1582 713 (0) 7 (1) 9 (2) 4 (3) para escribir el número 713,794. Diez años después el suizo Jost Bürgi escribió 713 794. Ese mismo año el italiano Magini sustituyó la circunferencia por un punto por 713.794. Y en cuanto a la coma de hoy, el neerlandés Wilbord Snellius inventó el XVII. principios del siglo: 713,794. La racionalización de la escritura de las fracciones facilitó la invención del sistema decimal de medición.

a.C. VI. Antes del siglo XX los matemáticos griegos conocían la existencia de los números irracionales: raíces 2, raíces 71, ... Los pitagóricos trataron de ocultar estos números (por no enfadarse a los dioses), pero luego aparecieron como “inmensos”. Sin embargo, debido a fallos en los sistemas de numeración no se definieron correctamente. Los matemáticos europeos, aprovechando los avances, se dieron cuenta de que eran números decimales inagotables (en los que no se repetían cifras). De esta manera consiguieron diferenciarse de los números racionales. Desde entonces surgió el concepto de números algebraicos y de números trascendentes. Hoy se distingue:

• Número irracional: que no es la solución de ninguna ecuación con un coeficiente global de primer orden: , e, erro 7, erro 10, …
• Número algebraico: solución de un coeficiente completo y una ecuación algebraica: Soluciones de las ecuaciones 2, erro 2, erro 7, ... x -2 = 0, x 2 - 2 = 0, x 3 - 7 = 0,...
• Número trascendente: coeficiente total o fraccionado y no solución de ecuación: , e, log 2, cos 25º,...

Aunque en el nuevo sistema se puede escribir cualquier número natural, los científicos han adoptado una escritura especial: 1000 = 10 3 ; 100.000 = 10 5 ; 82765900000000000 - 827659 x 10 11 o utilizando la escritura de la coma móvil 8,27659 x 10 16 .

Con el nuevo sistema se puede plazar una pregunta: ¿cuál es el número más grande que se puede escribir? Esta pregunta dio lugar al concepto de infinito. Hoy representamos el infinito con el símbolo. Fue utilizado por primera vez en 1655 por el inglés John Wallis. Hay que diferenciar el concepto físico y matemático del infinito. El mayor valor medido físicamente ha sido 1042. Es el número de protones y neutrones que hay en el universo entre otras cosas.

Los matemáticos han ido más lejos y han inventado números transfinitos. El primero de ellos es ¿ 0 (aleph-cero) (es la primera letra del alfabeto hebraico). Esto representa el número de números naturales, impares, pares, racionales, etc.

Los dos descubrimientos que permitieron el avance del álgebra fueron el nuevo sistema de cifras y la escritura simbólica lineal. Su inventiva (1591) se debe a François Viète. Viète generalizó el álgebra cuando expresó números desconocidos con x, y,... Éste liberó el álgebra y el pensamiento de los objetos concretos y contribuyó a aproximarse al razonamiento abstracto.

En cuanto a los símbolos, en la Edad Media el signo (-) se denominó minus y el signo (+) più. Las palabras fueron sustituidas por ñ y p, hasta que en 1489 el alemán Ricardo Widmann reconoció por primera vez los símbolos conocidos (+, -). En 1557 el inglés Robert Receke inventó el signo =, Thomas Harriot en 1631 en diferencias y símbolos, William Oughtred en x (multiplicación) XVII. A principios del siglo XX y (raíz cuadrada), símbolo (derivado de la letra R), fue creado por Christoph Rudolf en 1525.

Aquí termina esta pequeña historia de las cifras, una pequeña parte de la historia general del ser humano.