Història de les xifres (V)

1990/09/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Desplegament del nou sistema

El sistema hindú va trigar mil anys a arribar fins a Europa, on els àrabs van ser mediadors.

L'expansió àrab (VIII-XIII. Durant el segle XIX, tots els pobles van reunir obres gregues, filosòfiques, científiques o literàries i les arabicaron. En tots els llocs es van crear biblioteques i universitats. Bagdad, Dames i més tard les ciutats d'Alkairo, Kairuan, Fes, Granada i Còrdova es van convertir immediatament en centres científics.

A Europa XI. Fins al segle XX es va viure una crisi política i científica. Per exemple, per a ensenyar aritmètica teòrica, el Nicomaco de Geresa (d. C.) II. segle XX), inspirat per una obra matemàtica fluixa del grec Boecio (d. C.) En el segle V s'utilitzava una obra que s'atribuïa al llatí. Quant a l'aritmètica pràctica, manejaven la numeració romana i l'àbac.

Els àrabs, al principi, van assimilar la numeració alfabètica grega i hebrana i la van adaptar a l'alfabet dels seus 28 lletres. D'altra banda, es va recuperar el sistema de posició sexagesimal i el zero dels babilonis. Però quan van conèixer el sistema hindú a través de les relacions comercials, el van fer íntegrament.

Els àrabs no es van quedar en això i van aportar a la cultura. A l'hora de recopilar i traduir els treballs antics es van fer alguns comentaris. A més, la rigidesa de sistematització dels matemàtics grecs es va associar a la practicitat de la ciència hindú.

Entre els matemàtics àrab-islàmics destaca el samanés Mohamed Ibn Mussa al-Khowarizmi (780-850). És conegut pels seus dos llibres. En la primera es parla d'aritmètica i en ella s'explica el sistema hindú amb exemples. Posteriorment s'obriria amb èxit a l'Europa occidental. De fet, el nom llatí de l'autor es va convertir en el sinònim del sistema. En el seu segon treball va tractar la ciència algebraica. També va ser famós. El títol d'aquest treball començava amb la paraula alj. Una de les dues operacions que canviaven de secció els termes per a deixar termes positius en dues parts d'una equació es diu:

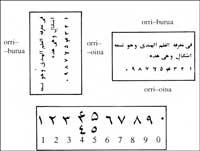
Quan els àrabs van conquistar el sistema hindú, no van fer més que copiar les xifres. Després de passar per les mans dels copistes van canviar d'aspecte.

Un motiu de canvi aparent es troba en l'escriptura, ja que escrivien per columnes, d'esquerra a dreta. Li donaven un gir de 90° per a llegir, en el sentit de les agulles del rellotge. No obstant això, van ser xifres que es van difondre per les províncies àrabs i que ells deien “hindi”.

Però les nostres xifres no procedeixen directament d'aquestes, sinó de les dels àrabs occidentals. IX. En el segle XVIII es va trencar l'imperi àrab-musulmà, quedant fora del califat de Bagdad l'Àfrica nord-occidental i la regió musulmana de la Península Ibèrica. No obstant això, les relacions no es van trencar, sobretot per peregrinacions fins a la Meca, intercanvis comercials, guerres i migracions de població. Els àrabs orientals van ensenyar als occidentals el sistema hindú. En aquesta regió les xifres van evolucionar de manera diferent.

Aquestes xifres es denominaven “ghobares” (xifres en pols) per la pols que s'escampava per a poder escriure les xifres en les taules de càlcul. Aquest canvi aparent es deu a la forma gràfica dels copistes occidentals.

Mentre els àrabs van conèixer el sistema hindú, van haver de passar segles perquè els europeus ho acceptessin. A l'Europa de l'època, des de l'abolició de l'Imperi romà fins al final de l'Edat mitjana, el càlcul (càlcul per àbac) estava en mans de privilegiats. No obstant això, els occidentals podien obtenir els avantatges del sistema hindú gràcies al monjo Gerbet d’Aurillac, que l'any 999 va ser nomenat Papa Silbestre II. En el convent Gerbert havia estudiat matemàtiques i astronomia. Durant la seva estada en la Península Ibèrica va estudiar el sistema de numeració i mètodes de càlcul dels àrabs. Com a director de l'escola diocesana de Reims va intentar aplicar els seus estudis. Però, desgraciadament, només va aconseguir introduir xifres (excepte zero). En els àbacs de columna es van substituir els cants per xifres, però en aquells àbacs no era necessari el zero.

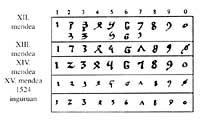
Igual que va ocórrer amb els àrabs, a Europa les xifres es van distorsionar per diferents motius; per escriure de fantasia, per copiar-les boca avall o indirectament, etc.

Després del pas de les creus es van recuperar les grafies originals. XIII. i XIV. A partir dels segles XVI es va convertir en la imatge actual. La impremta de Gutenberg va fixar per sempre les formes de les xifres. Si bé l'objectiu de les croades no era la reconquesta de la ciència i la cultura, va ser un dels resultats. Els croats que es van dirigir a Terra Santa van tornar amb la cultura local. Els croats van tenir intercanvis comercials i culturals amb els musulmans. Gràcies a ells el sistema hindú es va endinsar a Europa.

A l'altre costat de la mar Mediterrània, en la Península Ibèrica, XI. Des de finals del segle XX els intercanvis culturals es van enfortir gràcies a les obres dels traductors. Llavors els cristians van començar a traduir tots els treballs al llatí.

En aquest ambient va destacar un matemàtic italià: Leonardo de Pisa, anomenat “Fibonacci”. Va estudiar el sistema àrab a Àfrica musulmana i Orient Pròxim. Posteriorment, l'any 1202, va presentar el treball Liber Abaci (Tractat d'Abaco), en el qual explicava les regles del càlcul de xifres. A partir d'ara els afeccionats al nou càlcul es van multiplicar. No obstant això, el desenvolupament estava lluny.

Hi havia dues raons principals perquè no s'aprovés el nou càlcul. D'una banda, els “amos” de l'antic càlcul veien perillar la seva vida. D'altra banda, existia l'Església, que va demanar que el desenvolupament de la ciència dependera dels seus dogmes. La facilitat de càlcul dels àrabs va ser acusada a Satanàs.

També ens ajudarà l'etimologia de zero i xifres. La paraula zero prové de la paraula sanscrítica sifr (hutsa, hinduen sunya). Fibonacci, que en la seva obra Liber Abaci li va cridar zephirum, més tard es va convertir en cefiro i a partir de 1491 va quedar zero. Però de la paraula sifr també ve la paraula xifra. Les seves transcripcions en llatí Sifra, Xifra, Cyfra, Tzyphra, Xifri, Cyfre, etc. són. Al principi aquesta paraula va tenir el significat de zero. Per a entendre-ho cal tornar a l'ambient que marca l'Església. L'ús de xifres àrabs va estar prohibit en el seu moment. D'altra banda, la gent utilitzava el sistema ocult i va començar a denominar-se “xifra”, barrejant tots dos significats (zero i xifra). Els experts van tractar de mantenir el seu significat original, però no ho van aconseguir.

Els científics es van mostrar immediatament a favor del nou sistema. Als comerciants, banquers, funcionaris i en general endarrerits els va costar molt abandonar l'àbac. Situació durant l'Edat mitjana i el Renaixement XVII. i XVIII. Es va mantenir en les administracions fins als segles 20.

Es va acabar?

Finalment i després d'una llarga història d'obstacles, el nostre sistema es va completar. Però ha acabat la història de les xifres? Almenys així ho creiem. Malgrat canviar la grafia de les xifres quan apareixen els ordinadors, el seu nom no s'ha mogut. Podríem pensar en altres bases com les 12 o 2 (les dels ordinadors). No obstant això, el sistema no canviaria. Subsistirien el principi de posició, el zero i les regles de càlcul.

Des de l'època de l'home Crô-Magnon fins a l'home modern no hi ha hagut canvis bàsics en el cervell, sinó riquesa cultural. El matemàtic Leopoldo Kronecker va dir: “Déu va crear el nombre natural, la resta obra humana”. O en paraules del filòsof alemany Lichtenberg: “L'home va començar des del principi: tota magnitud és igual a si mateix, i va arribar a mesurar el Sol i les estrelles”.

La teoria de la visita d'éssers d'altres mons ha fallat en aquest camp. Si eren tan ràpids, per què no ens van deixar la numeració de posició i el zero?

En xifres no hi ha torre de Babel. Mentre a tot el món hi ha més de quatre mil llengües i desenes d'alfabets, en l'actualitat tots els pobles han acceptat el sistema de xifres hindú.

Aquest sistema ha permès la creació i desenvolupament de calculadores i tractament de la informació. Això no hauria estat possible amb altres sistemes. Al principi Leonardo de Vinci, Pascal, Leibniz, Babbage,... (mecànica) més tard Hallerith, Torres Quevedo, Arken,... (electromecànica) i finalment Turing, Atanasoff, Von Neumann,... Això es deu a la labor realitzada pels científics (electrònica).

Al costat de les xifres es va desenvolupar el concepte numèric i l'escriptura matemàtica.

Durant molt de temps no es podien escriure números negatius, ni tampoc remissions com 4 - 7. El concepte zero va donar aquesta oportunitat.

Un altre assoliment ha estat definir i unir conceptes diferents. Per exemple, les fraccions. Es coneixen des de l'antiguitat. Els egypti només coneixien les fraccions originals (quan el numerador és 1). Els babilonis van donar a les fraccions una redacció racional, creant fraccions sexagesimals. Els grecs, davant la impossibilitat de la seva numeració alfabètica, van adoptar el sistema babilònic. L'escriptura moderna es deu als hindús i la invenció de la línia als àrabs.

Posteriorment, el descobriment de les fraccions decimals (quan el divisor és la reversió decimal) va permetre escriure xifres a la dreta de la coma. A Europa, el primer va ser el belga Simón Stevin, que va escriure en 1582 713 (0) 7 (1) 9 (2) 4 (3) per a escriure el número 713,794. Deu anys després el suís Jost Bürgi va escriure 713 794. Aquest mateix any l'italià Magini va substituir la circumferència per un punt per 713.794. I quant a la coma d'avui, el neerlandès Wilbord Snellius va inventar el XVII. principis del segle: 713,794. La racionalització de l'escriptura de les fraccions va facilitar la invenció del sistema decimal de mesurament.

a. C. VI. Abans del segle XX els matemàtics grecs coneixien l'existència dels nombres irracionals: arrels 2, arrels 71, ... Els pitagòrics van tractar d'ocultar aquests números (per no enfadar-se als déus), però després van aparèixer com a “immensos”. No obstant això, a causa de fallades en els sistemes de numeració no es van definir correctament. Els matemàtics europeus, aprofitant els avanços, es van adonar que eren nombres decimals inesgotables (en els quals no es repetien xifres). D'aquesta manera van aconseguir diferenciar-se dels nombres racionals. Des de llavors va sorgir el concepte de nombres algebraics i de nombres transcendents. Avui es distingeix:

• Nombre irracional: que no és la solució de cap equació amb un coeficient global de primer ordre: , e, erro 7, erro 10, …
• Nombre algebraic: solució d'un coeficient complet i una equació algebraica: Solucions de les equacions 2, erro 2, erro 7, ... x -2 = 0, x 2 - 2 = 0, x 3 - 7 = 0,...
• Nombre transcendent: coeficient total o fraccionat i no solució d'equació: , e, log 2, cos 25è,...

Encara que en el nou sistema es pot escriure qualsevol nombre natural, els científics han adoptat una escriptura especial: 1000 = 10 3 ; 100.000 = 10 5 ; 82765900000000000 - 827659 x 10 11 o utilitzant l'escriptura de la coma mòbil 8,27659 x 10 16 .

Amb el nou sistema es pot plazar una pregunta: quin és el número més gran que es pot escriure? Aquesta pregunta va donar lloc al concepte d'infinit. Avui representem l'infinit amb el símbol. Va ser utilitzat per primera vegada en 1655 per l'anglès John Wallis. Cal diferenciar el concepte físic i matemàtic de l'infinit. El major valor mesurat físicament ha estat 1042. És el nombre de protons i neutrons que hi ha en l'univers entre altres coses.

Els matemàtics han anat més lluny i han inventat números transfinits. El primer d'ells és 0 (aleph-zero) (és la primera lletra de l'alfabet hebraico). Això representa el nombre de nombres naturals, imparells, parells, racionals, etc.

Els dos descobriments que van permetre l'avanç de l'àlgebra van ser el nou sistema de xifres i l'escriptura simbòlica lineal. La seva inventiva (1591) es deu a François Viète. Viète va generalitzar l'àlgebra quan va expressar números desconeguts amb x, i,... Aquest va alliberar l'àlgebra i el pensament dels objectes concrets i va contribuir a aproximar-se al raonament abstracte.

Quant als símbols, en l'Edat mitjana el signe (-) es va denominar minus i el signe (+) più. Les paraules van ser substituïdes per ñ i p, fins que en 1489 l'alemany Ricardo Widmann va reconèixer per primera vegada els símbols coneguts (+, -). En 1557 l'anglès Robert Receke va inventar el signe =, Thomas Harriot en 1631 en diferències i símbols, William Oughtred en x (multiplicació) XVII. A principis del segle XX i (arrel quadrada), símbol (derivat de la lletra R), va ser creat per Christoph Rudolf en 1525.

Aquí acaba aquesta petita història de les xifres, una petita part de la història general de l'ésser humà.