¿Ultrafero olvidado o la gente sabe quién es el momento lineal?

Hay magnitudes físicas muy conocidas, como la velocidad, la fuerza, la potencia, el trabajo, la energía… que son muy famosas y que son conocidas no sólo por los científicos, sino por cualquier otro.
¿Velocidad? Sí, claro, indica la rapidez de los desplazamientos, en metros por segundo, o en kilómetros por hora, para medir los movimientos de los automóviles (y poner multas), etc.
¡Fuerza! ¿Quién no conoce la fuerza? Los harrijasotzailes tienen algo terrible, los remeros también actúan a tope… la unidad de fuerza lleva el nombre del famoso Newton, aunque es una combinación de unidades simples: kg·m/s2.
¡Potencia! Honorable… ¡La magnitud sagrada con la que valoramos aparatos e instrumentos! Los automóviles necesitan lo máximo posible, los aparatos domésticos también… La unidad es el vatio (kg·m2/s3) y la unidad de potencia equina equivalente…
Trabajo o energía. Eso también es bastante prestigioso. A veces resulta algo confuso porque hay muchos tipos de energía: potencial, cinética...; todos los tipos de energía tienen la misma unidad, otra denominación digna: el julio (kg·m2/s2).
Algo más escondido que esas magnitudes tan famosas, existe otra magnitud física, más desconocida que las mencionadas; no es famosa… casi nadie la menciona. Siempre se dedica a trabajos ocultos. Siempre a oscuras y nadie se da cuenta de ello. Sin embargo, es una magnitud física de gran importancia. Más importante que casi todos. Merece la pena ser citado y tratado con amabilidad.
Antiguamente se le denominaba cantidad de movimiento, pero en la actualidad ha prevalecido otro nombre: momento lineal o P. Multiplica la masa y la velocidad de los cuerpos: M·V. Es un vector, es decir, tiene una dirección, la misma dirección que la velocidad. La unidad del momento lineal (kg·m/s) nunca ha merecido la pena, al parecer, el nombre de algún físico reconocido, ya que no tiene ni nombre corto ni nombre, por el momento.Pues bien, el momento lineal gobierna las interacciones entre los cuerpos. Es dueña de interacciones entre cuerpos. Yo diría Dios. Aunque el cuerpo vaya, venga, choce, parta, explota, pegue o tenga cualquier tipo de interacción, el momento lineal se mantiene: P = cte. No cambia de cualquier manera. Mantiene el valor. Vale lo mismo si tenemos en cuenta todo el conjunto aislado de todos los cuerpos que intervienen (lo que se debe a la ley de acción y reacción de Newton, según la cual si un cuerpo ejerce una fuerza sobre otro, el otro ejerce una fuerza del mismo valor sobre el primero, pero en sentido contrario: SIEMPRE).
Ten en cuenta que cuando un cuerpo de cualquier tipo atrae o repele a otro, pase lo que pase entre ambos, no consiguen cambiar el momento lineal total. Por ejemplo:
Supongamos que dos patinadores están juntos, parados y de repente se empujan unos a otros (da igual que uno empuje al otro, o viceversa, o ambos se empujan mutuamente).
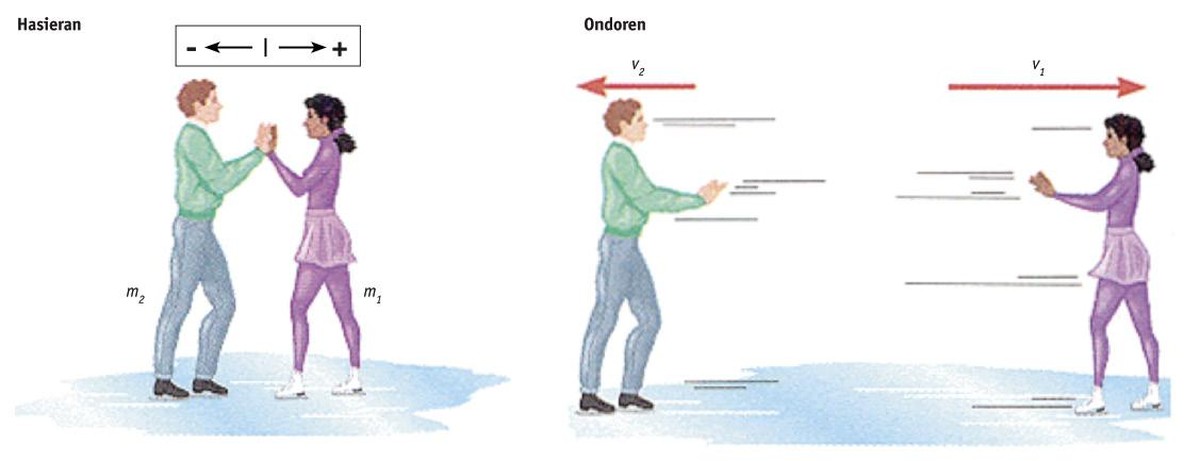
Anotemos el valor del momento lineal, el producto de las masas y de las velocidades:
Inicialmente (antes del empuje), Phas= m1·0 + m2·0 = 0 es nulo porque los dos patinadores están parados.
A continuación, ?= m1·v1 + m2·v2
El momento lineal no cambia, por lo que Phas= ? o bien: 0 = m1·v1 + m2·v2;
Con un poco de matemática elemental se puede escribir la siguiente expresión:
v2/v1 = - m1/m2
Por ejemplo, si los dos patinadores tienen la misma masa (m1 = m2) y uno de ellos, por empuje, toma una velocidad de 1 m/s, el otro alcanzará una velocidad de –1 m/s (igual valor pero en sentido contrario). O si una a 5 m/s, la otra a 5 m/s. Asimismo, si un patinador tiene la mitad de la masa (m1/m2 = 0,5), detectará el doble de velocidad v1/v2 = 2. Siempre más rápido (el menos masivo). En función de la proporción de las masas, las velocidades serán justamente inversas.
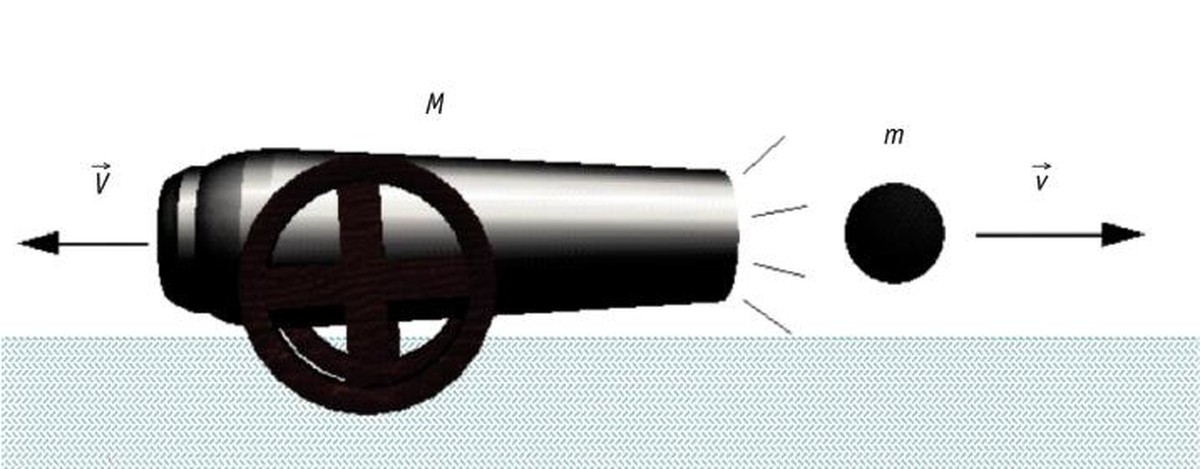
Por ejemplo, cuando una escopeta o un cañón disparan, si la relación de masas es M/m = 100 y se sabe que la velocidad de la bala es v = 100 m/s, la velocidad del cañón hacia atrás será: V = 1 m/s.Esta velocidad de retroceso del cañón es inevitable porque el momento lineal así lo establece la ley de acción y reacción de Newton; incluso cuando lancemos algo, el proyectil nos empujará hacia atrás.
En la misma línea, supongamos que dos coches chocan entre sí y quedan pegados. ¿Cómo saber hacia dónde se moverán tras el choque? Aplicando de nuevo la conservación del momento lineal:
P antes = m1·v1 + m2·v2 Después = m1·V + m2·V;
Si quedan adheridos, ambos tendrán la misma velocidad (V).
Escribir después Pllehen = P, de donde se puede calcular la velocidad V después del choque:
m1 v1 + m2·v2 = (m1 + m2)·V; V = (m1v1 + m2·v2) / (m1 + m2)
Incluso pueden quedar paradas en determinadas condiciones: la misma masa y velocidades de igual valor (de sentido contrario), o la doble masa y la mitad de la velocidad, etc., pudiendo combinarse con condiciones previas al impacto.

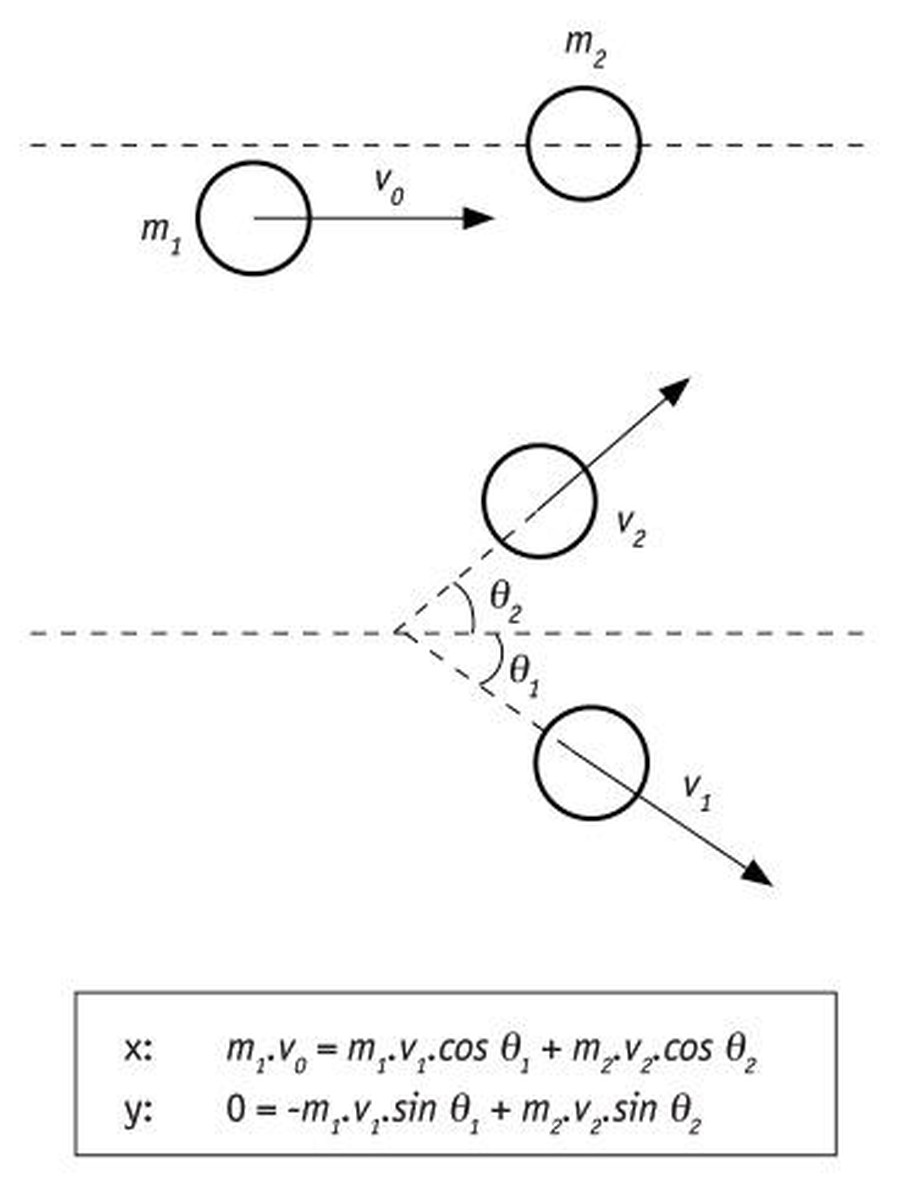
Es más, como el momento lineal tiene carácter vectorial, también gobierna los choques entre bolas de billar [1].

Este carácter vectorial se analiza en dos direcciones convencionalmente (x e y) y estudiando por separado las dos proyecciones del momento lineal. Ser P constante significa que ambas proyecciones deben ser constantes a la vez:
Px= cte. y Py = cte.
En el caso de patinadores, balas de cañón, coches o bolas de billar, sólo dos cuerpos han participado en la interacción, pero pueden existir más cuerpos, y entonces se conserva el momento lineal total, como los fuegos artificiales. En el momento de la explosión, si el explosivo está parado, la suma de los momentos lineales de todas las partes (explosiones simétricas) debe ser igual a cero.

Por el contrario, si el artefacto estaba en movimiento en el momento de la explosión, después de la explosión el momento lineal debe ser el mismo entre todos los compartimentos, y no sale la explosión simétrica, sino la dirección que llevaba antes.
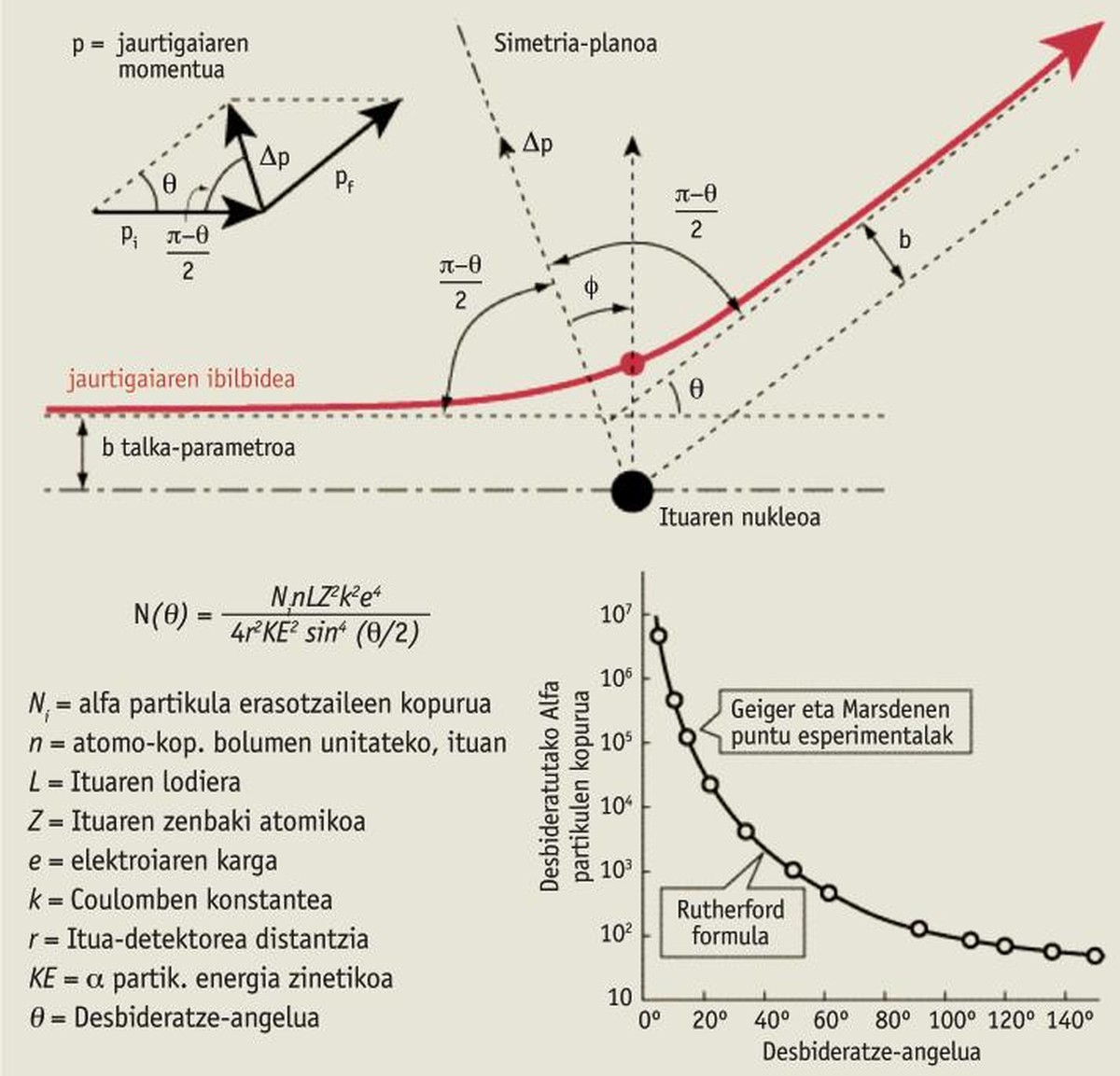
La capacidad del momento lineal abarca todos los ámbitos de la física, desde el nivel microscópico hasta el nivel astronómico. Desde choques o explosiones entre asteroides y planetas hasta interátomos. Por ejemplo, en el intento de comprender y explicar la estructura de los átomos, Ernest Rutherford descubrió el núcleo de los átomos en 1911 gracias a la “conservación del momento lineal”.
Así, Rutherford descubrió los rayos alfa en la radiación emitida por los elementos radiactivos (carga eléctrica positiva y energía muy elevada), descubriendo posteriormente que son núcleos de helio, unidos a dos protones y dos neutrones, y, para conocer mejor estas partículas alfa, se le ocurrió lanzar una gama de rayos alfa contra un fino papel de oro. Así lo prometió a dos jóvenes estudiantes: Hans Geiger y Ernest Marsden. Esperaban que aquel poderoso rayo atravesara de lado a lado aquel fino papel de oro, aunque quizás se desviara un poco. El resultado fue sorprendente. Casi todas las partículas alfa tuvieron un recorrido correcto, tal y como se esperaba, pero algunas de ellas se desviaron enormemente y otras ¡incluso rebotaron hacia atrás! ¡Sorprendente! “Lanza un cañonazo contra una fina capa de papel y rebota balas de cañón! !” [2].
La explicación teórica de Rutherford y el ejemplo de las bolas de billar son muy similares, aplicando la conservación del momento lineal, y es perfectamente coherente con los resultados de este experimento (ver cuadro adjunto).
Las conclusiones de esta investigación revolucionaron la estructura del átomo: los átomos deben tener un pequeño centro, el núcleo (unos 10-14 m). Este núcleo debe tener carga eléctrica positiva y casi toda la masa del átomo, y a su alrededor, dejando casi todo el espacio vacío, los electrones deben estar [3]. Si no hubiera aplicado la conservación del momento lineal, no hubiera podido obtener tal efecto.
Además de este importante descubrimiento del núcleo del átomo, la conservación del momento lineal ha traído consigo otros muchos descubrimientos.
El propio Rutherford postuló el neutrón en 1920 recogiendo las masas y velocidades de los productos que se producen en las desintegraciones radiactivas, pero no encontró neutrón, ya que al no tener carga eléctrica es difícil encontrar la huella de neutrones. Doce años después, en 1932, J. El físico inglés Chadwick descubrió experimentalmente estos neutrones. Siempre en los cálculos de desintegración se tiene en cuenta el momento lineal, como en el caso de los patinadores [4].
En 1923, A. El estadounidense Compton demostró que, además de las partículas de materia, la radiación electromagnética también tiene un momento lineal y sirvió para reforzar el modelo corpuscular de los fotones creados en los últimos años. La demostración teórica del efecto Compton utiliza también la conservación del momento lineal, como las bolas de billar [5].
Wolfgang Pauli utilizó también la conservación del momento lineal en 1930 para postular la partícula denominada neutrino. Y en 1956, C. Cowan y F. Fue descubierto por Reines [6].
Al comienzo de este artículo he mencionado la lista de las magnitudes físicas más prestigiosas (velocidad, fuerza, potencia…). No quisiera quitar importancia, pero creo que en la parte superior de esa famosa lista habría que incluir otra magnitud: el momento lineal. Esta magnitud no es suficientemente conocida (ultraprecisión olvidada) y, según hemos visto más adelante, debería ocupar un lugar entre las magnitudes físicas más prestigiosas.
Bibliografía
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian