Ultrafero forgotten or do people know who the linear moment is?

There are well-known physical magnitudes, such as speed, force, power, work, energy... that are very famous and are known not only by scientists, but by any other.
Speed? Yes, of course, it indicates the speed of travel, in meters per second, or in kilometers per hour, to measure the movements of cars (and put fines), etc.
Force! Who does not know strength? The harrijasotzailes have something terrible, the rowers also act butt... the force unit is named after the famous Newton, although it is a combination of simple units: kg·m/s2.
Power! Honorable… The sacred magnitude with which we value devices and instruments! Cars need as much as possible, household appliances also… The unit is the watt (kg·m2/s3) and equine power unit equivalent…
Work or energy. That is also quite prestigious. Sometimes it is confusing because there are many types of energy: potential, kinetic...; all types of energy have the same unit, another worthy denomination: July (kg·m2/s2).
Something more hidden than those famous magnitudes, there is another physical magnitude, more unknown than those mentioned; it is not famous... almost nobody mentions it. Always dedicated to hidden jobs. Always in the dark and nobody realizes it. However, it is a physical magnitude of great importance. More important than almost all. It is worth being quoted and treated with kindness.
Formerly it was called the amount of movement, but at present another name has prevailed: linear moment or P. Multiply the mass and speed of the bodies: M·V. It is a vector, that is, it has a direction, the same direction as speed. The unity of the linear moment (kg·m/s) has never been worth, apparently, the name of some recognized physicist, since it has neither short name nor name, for the moment.Well, the linear moment governs the interactions between bodies. It owns interactions between bodies. I would say God. Although the body goes, comes, collides, breaks, explodes, sticks or has any type of interaction, the linear moment remains: P = cte. It does not change in any way. It keeps the value. It is the same if we take into account the whole isolated set of all the intervening bodies (which is due to Newton's law of action and reaction, according to which if one body exerts one force on another, the other exerts a force of the same value on the first, but in the opposite sense: ALWAYS).
Keep in mind that when a body of any kind attracts or repels another, whatever happens between the two, they fail to change the total linear moment. For example:
Suppose two skaters are together, standing up and suddenly pushing each other (no matter what one pushes the other, or vice versa, or both push each other).
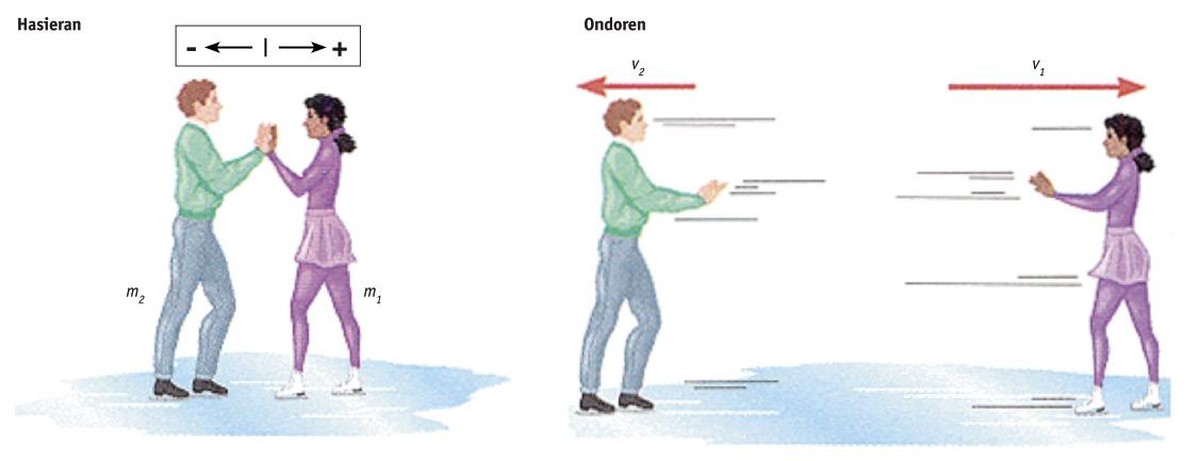
Note the value of the linear moment, the product of masses and speeds:
Initially (before the push), Phas= m1·0 + m2·0 = 0 is zero because the two skaters are standing.
Then, ?= m1·v1 + m2·v2
The linear moment does not change, so Phas= ? or: 0 = m1·v1 + m2·v2;
With some elementary mathematics you can write the following expression:
v2/v1 = m1/m2
For example, if the two skaters have the same mass (m1 = m2) and one of them, by push, takes a speed of 1 m/s, the other will reach a speed of –1 m/s (equal value but in the opposite direction). Or if one at 5 m/s, the other at 5 m/s. Also, if a skater has half the mass (m1/m2 = 0.5), it will detect twice the speed v1/v2 = 2. Always faster (the least massive). Depending on the proportion of the masses, the speeds will be just reverse.
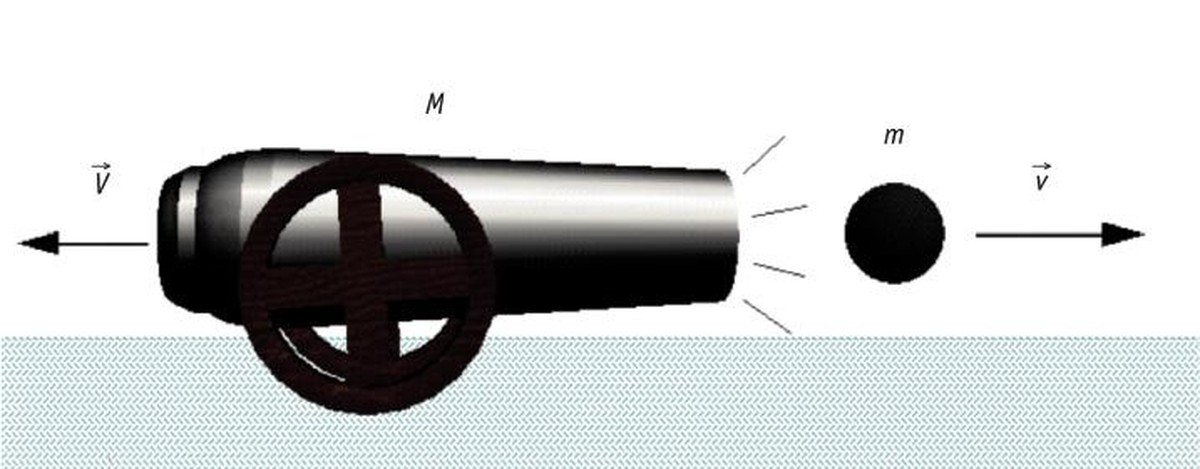
For example, when a shotgun or cannon fire, if the mass ratio is M/m = 100 and it is known that the speed of the bullet is v = 100 m/s, the speed of the cannon back will be: V = 1 m/s.This reverse speed of the cannon is inevitable because the linear moment is established by Newton's law of action and reaction; even when we throw something, the projectile will push us back.
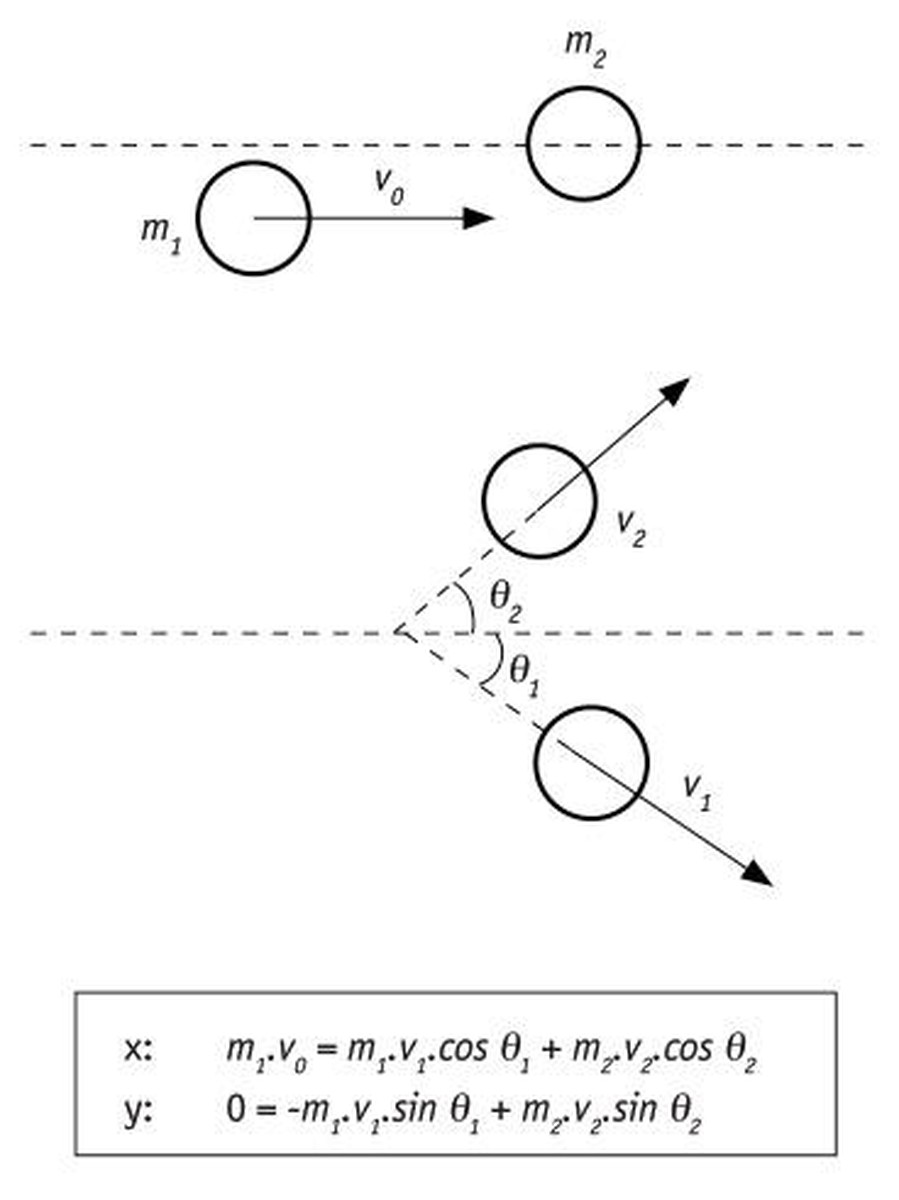
On the same line, suppose two cars collide with each other and are stuck. How to know where they will move after the crash? Applying the conservation of the linear moment again:
P before = m1·v1 + m2·v2 After = m1·V + m2·V;
If they are attached, both will have the same speed (V).
Write then Pllehen = P, from where you can calculate the speed V after the crash:
m1 v1 + m2·v2 = (m1 + m2)·V; V = (m1v1 + m2·v2) / (m1 + m2)
They can even stand in certain conditions: the same mass and speeds of equal value (in the opposite direction), or the double mass and half of the speed, etc., and can be combined with pre-impact conditions.

Moreover, since the linear moment has vector character, it also governs the shocks between billiard balls [1].

This vector character is analyzed in two directions conventionally (x and y) and studying separately the two projections of the linear moment. Constant P means that both projections must be constant at once:
Px= cte. and Py = cte.
In the case of skaters, cannon balls, cars or billiard balls, only two bodies have participated in the interaction, but there can be more bodies, and then the total linear moment, such as fireworks, is preserved. At the time of the explosion, if the explosive is stopped, the sum of the linear moments of all parts (symmetrical explosions) must be zero.

On the contrary, if the artifact was in motion at the time of the explosion, after the explosion the linear moment must be the same among all the compartments, and the symmetric explosion does not come out, but the direction it had before.
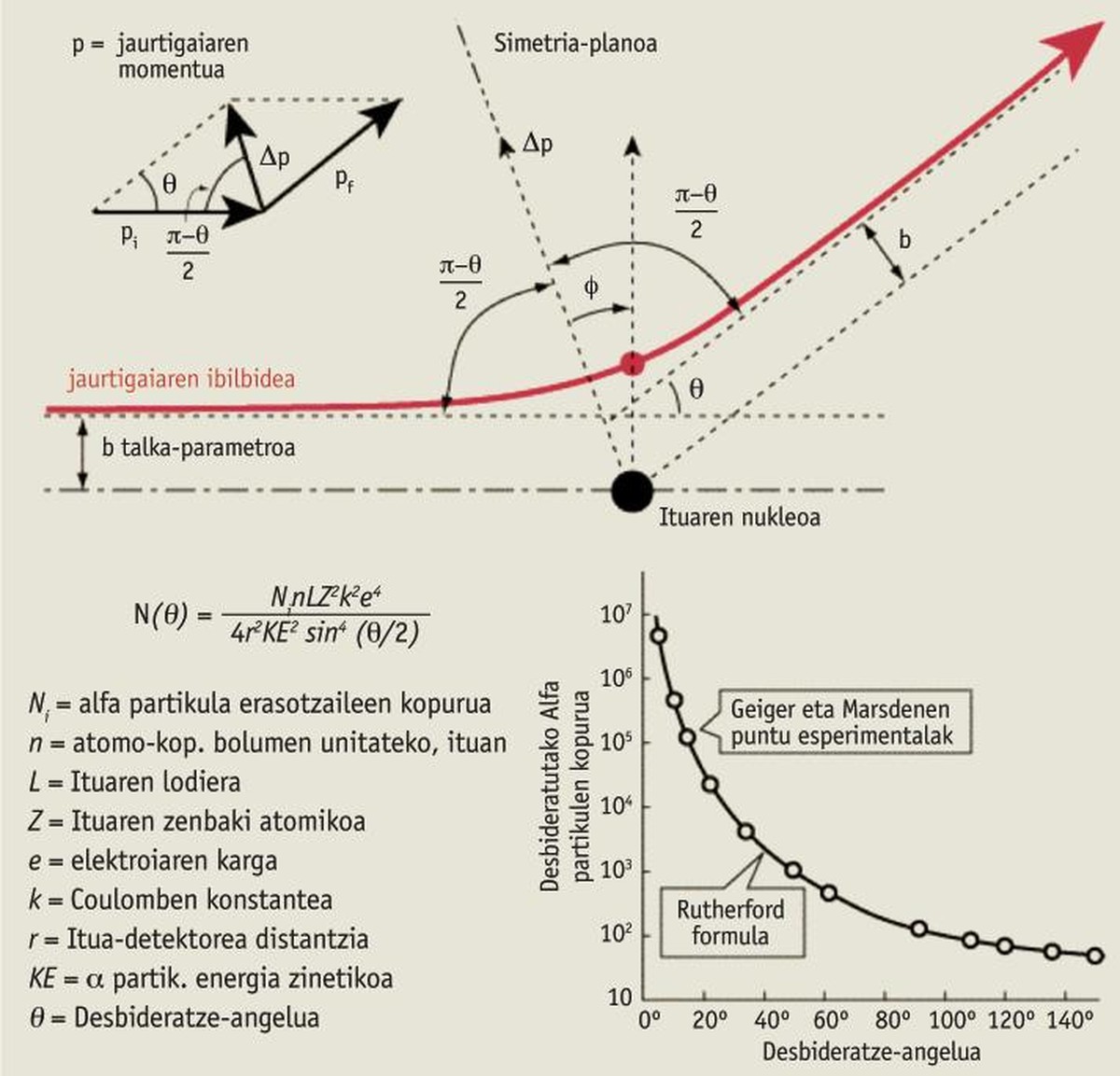
The ability of the linear moment encompasses all areas of physics, from the microscopic level to the astronomical level. From collisions or explosions between asteroids and planets to interatoms. For example, in an attempt to understand and explain the structure of atoms, Ernest Rutherford discovered the nucleus of atoms in 1911 thanks to the “conservation of the linear moment”.
Thus, Rutherford discovered the alpha rays in the radiation emitted by the radioactive elements (positive electric charge and very high energy), later discovering that they are nuclei of helium, attached to two protons and two neutrons, and, to know better these alpha particles, it occurred to him to launch a range of alpha rays against a thin golden paper. He promised two young students: Hans Geiger and Ernest Marsden. They expected that powerful ray to cross the fine golden paper from side to side, even if it might be diverted a little. The result was surprising. Almost all alpha particles had a correct course, as expected, but some of them diverted greatly and others even bounced back! Amazing! “Throw a shot at a thin layer of paper and bounce cannon balls! 2.
Rutherford's theoretical explanation and the example of billiard balls are very similar, applying linear moment conservation, and is perfectly consistent with the results of this experiment (see attached table).
The conclusions of this research revolutionized the structure of the atom: the atoms must have a small center, the nucleus (about 10-14 m). This nucleus must have positive electric charge and almost the entire mass of the atom, and around it, leaving almost all the space empty, the electrons must be [3]. If he had not applied the conservation of the linear moment, he could not have obtained such an effect.
In addition to this important discovery of the nucleus of the atom, the conservation of the linear moment has brought with it many other discoveries.
Rutherford himself postulated neutron in 1920 collecting the masses and velocities of products that occur in radioactive disintegrations, but he did not find neutron, since having no electric charge it is difficult to find the neutron footprint. Twelve years later, in 1932, J. The English physicist Chadwick experimentally discovered these neutrons. The linear moment is always taken into account in disintegration calculations, as in the case of skaters [4].
In 1923, A. The American Compton demonstrated that, in addition to matter particles, electromagnetic radiation also has a linear moment and served to reinforce the corpuscular model of photons created in recent years. The theoretical demonstration of the Compton effect also uses the conservation of the linear moment, as the billiard balls [5].
Wolfgang Pauli also used the conservation of the linear moment in 1930 to postulate the particle called neutrino. And in 1956, C. Cowan and F. It was discovered by Reines [6].
At the beginning of this article I mentioned the list of the most prestigious physical magnitudes (speed, strength, power…). I don't want to remove importance, but I think that at the top of that famous list would have to include another magnitude: the linear moment. This magnitude is not sufficiently known (ultraprecision forgotten) and, as we have seen later, should occupy a place among the most prestigious physical magnitudes.
Bibliography
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian