Problema abierto

1992/11/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

inquemos la circunferencia de diámetro 1. A su alrededor representaremos polígonos inscritos y circunscritos que no serán normales.

Ramón Urkola me propuso este problema.

Fijemos una circunferencia de diámetro 1. A su alrededor representaremos polígonos inscritos y circunscritos que no serán normales. Seguiremos el siguiente procedimiento: representaremos el polígono circunscrito de la zona k y calcularemos su perímetro P0(k). En el segundo paso tomaremos este perímetro P0(k) como el número de lados de los nuevos polígonos inscritos y circunscritos y calcularemos sus nuevos perímetros; P1(k) y P1(k); P1(k) como el número de lados de los dos nuevos polígonos, P1(k) y P2(Pk). Continuando de esta forma obtenemos dos secuencias de polígonos y sus correspondientes perímetros:

Inscrita: P0, p1(k), p2(k), ..., pn(k), ...Circunscrita: P0, P1, P2, ..., Pn(k), ...

Recordar que cada Pn(k) tiene dos significados: el perímetro de un polígono circunscrito y el número de lados de los siguientes polígonos inscritos y circunscritos.

La pregunta es ¿tienen límites estas dos secuencias?.

Cabe destacar que los polígonos que aparecen aquí son “polígonos teóricos”. De hecho, el perímetro Pn(k) es un número real que no tiene por qué ser siempre un número normal. Por ejemplo, mirando al tablero, cuando cogemos k = 3,5950 nos aparece un polígono de 3,5950. Eso no es un polígono muy común, claro.

Nº(s) de interiores3.01005,173,594,83,83,83,82,83,82,83,83,82,83,83,82,83,83,82,83,82,83,82,83,82,83,82,83,82,82,83,82,83,83,82,83,82,83,83,82,83,83,82,83,83,83,83,83,82,83,83,83,83,83,83,83,83,83,83,82,83,83,83,83,82,83,83,83,83,83,83,83,82,82,83,82,83,83,83,82,82,83,83,83,82,82,83,83,82,83,83,83,83,83,82,82,83,83,83,83,83,82,83,83,83,83,82,82,83,82,82,83,83,82,82,83,83,83,83,83,83,

Para calcular el perímetro de los polígonos es necesario conocer el ángulo central. Aprovechamos para ampliar el concepto de polígono: los polígonos regulares de m (normal) pueden dividirse en m triángulos isósceles, con un ángulo ? = 2p/m formado por las mismas caras. En este problema tomaremos el número m real.

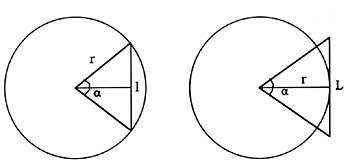
Las fórmulas de los perímetros de los polígonos inscritos y circunscritos son: ángulo central correspondiente a los polígonos ?; longitudes de los lados de los polígonos l; número de lados k y radio r.

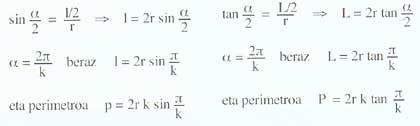
Ramón Urkola obtuvo los datos que aparecen en la tabla. El primer número de diferencias que eligió para iniciar la secuencia fue k = 3,0100. A partir de ahí calcula los perímetros P0 = 2,6014 y P0 = 5,1718. En la siguiente k = 5,1718, obteniendo p1 = 2,9519 y P1 = 3,5950. Así consiguió todos los siguientes perímetros.

Analizando la tabla se observa que la sucesión perimetral pn oscila alrededor de 2,82... Lo mismo ocurre con el perímetro Pn y el número 4. Eso nos da la pista. 2,82... (o más concretamente 2) 2) y 4 son los límites de las series Pn y Pn? En ambos casos, los perímetros 2 y 4 corresponden a cuadrados inscritos y circunscritos.

En esta circunferencia, de diámetro 1, los perímetros de los polígonos inscritos se dirigen hacia el valor 2, es decir, se obtiene un polígono de 2 perímetros (número de lados). Este polígono es cuadrado. Los perímetros de los polígonos circunscritos tienen como límite el valor 4. Este valor también corresponde a un cuadrado. En ambos casos las aproximaciones se producen alternando valores más o menos aproximados (ver tabla).

La siguiente pregunta es que el diámetro de la circunferencia está estrechamente unido a los perímetros de los polígonos. Por lo tanto, ¿se obtendrán diferentes resultados para distintos diámetros?, ¿cuál es la relación entre diámetro y límites?

Otra pregunta, si en lugar de tomar como número de lados los perímetros de los polígonos circunscritos los inscritos, ¿qué resultado obtendríamos?.

Por último, ¿puede ser cualquiera el número de primeros lados que se elija para iniciar las secuencias de perímetros?.