Open problem

1992/11/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

inquemos the circumference of diameter 1. Around it we will represent inscribed and circumscribed polygons that will not be normal.

Ramón Urkola proposed this problem to me.

We fix a diameter circumference 1. Around it we will represent inscribed and circumscribed polygons that will not be normal. We will follow the following procedure: we will represent the circumscribed polygon of zone k and calculate its perimeter P0(k). In the second step we will take this perimeter P0(k) as the number of sides of the new inscribed and circumscribed polygons and calculate their new perimeters; P1(k) and P1(k); P1(k) as the number of sides of the two new polygons, P1(k) and P2(Pk). Continuing in this way we obtain two sequences of polygons and their corresponding perimeters:

Registered: P0, p1(k), p2(k), ..., pn(k), ...Circumscribed: P0, P1, P2, .., Pn(k), ...

Remember that each Pn(k) has two meanings: the perimeter of a circumscribed polygon and the number of sides of the following inscribed and circumscribed polygons.

The question is, do these two sequences have limits?

It should be noted that the polygons that appear here are “theoretical polygons”. In fact, the Pn(k) perimeter is a real number that does not have to always be a normal number. For example, looking at the board, when we take k = 3,5950 we see a polygon of 3,5950. That is not a very common polygon, of course.

3,82,83,83,82,83,83,83,83,83,83,83,83,83,83,83,83,82,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,82,83,83,83,83,83,83,82,83,83,83,83,83,83,83,83,83,82,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,82,83,83,83,83,82,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,8

To calculate the perimeter of the polygons it is necessary to know the central angle. We use to expand the polygon concept: regular m (normal) polygons can be divided into m isosceles triangles, with a <unk> = 2p/m angle formed by the same faces. In this problem we will take the actual number m.

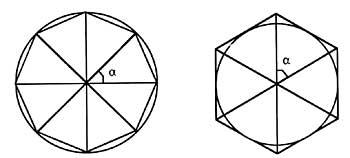
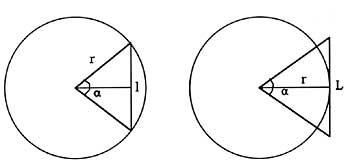
The formulas of the perimeters of the inscribed and circumscribed polygons are: central angle corresponding to the <unk> polygons; lengths of the sides of the l polygons; number of k sides and r radius.

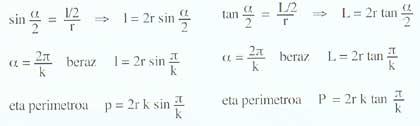
Ramón Urkola obtained the data that appear in the table. The first number of differences you chose to start the sequence was k = 3,0100. From there he calculates the perimeters P0 = 2,6014 and P0 = 5,1718. In the next k = 5,1718, obtaining p1 = 2,9519 and P1 = 3,5950. Thus he got all the following perimeters.

Analyzing the table it is observed that the perimeter succession pn oscillates around 2.82... The same goes for the Pn perimeter and number 4. That gives us the clue. 2.82... (or more specifically 2) 2) and 4 are the limits of the Pn and Pn series? In both cases, perimeters 2 and 4 correspond to inscribed and circumscribed squares.

In this circumference, of diameter 1, the perimeters of the inscribed polygons are directed towards value 2, that is, a polygon of 2 perimeters (number of sides) is obtained. This polygon is square. The perimeters of the circumscribed polygons have as limit the value 4. This value also corresponds to a square. In both cases the approximations occur by alternating more or less approximate values (see table).

The next question is that the diameter of the circumference is closely attached to the perimeters of the polygons. Therefore, will different results be obtained for different diameters?, What is the relationship between diameter and limits?

Another question, if instead of taking as number of sides the perimeters of the polygons circumscribed those inscribed, what result would we get?.

Finally, can anyone be the number of first sides chosen to start perimeter sequences?