Poliminos (I)

1990/01/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

A palabra omino provén do Dominus latino e significa Jaun. Con todo, nós inventaremos outra orixe: Domino = dous minos.

Trátase dun popular xogo de 28 pezas dominou. A palabra dominou provén do Latín e significa Jaun. Con todo, nós inventaremos outra orixe: Domino = dous minos. É dicir, Dominou podería significar dous minos. Mirando as pezas do xogo, descubrirás que todas están formadas por dous cadros. Por tanto, seguindo a nosa hipótese, a palabra mino correspondería á palabra cadrado.

Esta será a escusa paira construír outros poliminos desde o dominou. A partir de agora esquecerémonos do xogo dominical e ocuparémonos da súa estrutura, sempre baixo a hipótese de que "mino = cadrado".

Engadindo dous minos obtense una peza. A peza parece ser única aínda que se engadan de calquera xeito. A esta peza chamarémoslle dominou e ao ser única en forma non dá moito xogo.

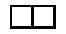
Antes de seguir adiante, avisámosche de que as pezas obtidas a través de todas as simetrías (no plano) e xiros (no plano e no espazo) posibles son iguais. Posteriormente porémoslle un exemplo para que o entenda facilmente.

Abordemos a construción de triminos. Paira iso engadimos un mino máis ao dominou, obtendo dous triminos diferentes:

Os triminos tampouco nos dan moito xogo. Con todo, con estas dúas pezas pódense realizar varias figuras, como se ve a continuación:

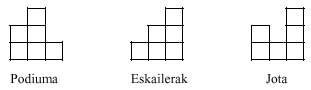
Con todo, non é posible realizar un rectángulo de 2x3, como se pode comprobar facilmente.

Podemos pasar, por tanto, á seguinte, os tetraminos. Paira a formación dos tetraminos, imos reter o trimino de todos os xeitos:

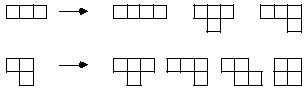
Restando os mesmos obtéñense cinco tetraminos diferentes:

O cinco tetraminos recollen un total de 20 minos. Con elas pódense realizar rectángulos de 2x10 e 4x5. Con todo, ningún do cinco tetraminos pode completarse. Pola contra, si con cinco pezas pódense realizar as seguintes imaxes:

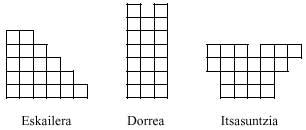
Avanzemos formando pentaminos. De novo retomamos os tetraminos cun mino, de todos os xeitos:

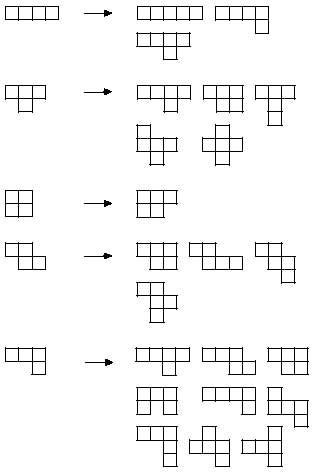
Seleccionando só diferentes, obtense 12 pentaminos:

Vexamos agora o exemplo inicialmente prometido:

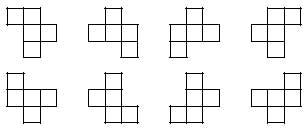
Consideramos todas as pezas que aparecen na imaxe como iguais.

Con 12 pentaminos recóllense 60 minos que permiten realizar rectángulos de 2x30, 3x20, 4x15, 5x12 e 6x10. Está claro que o primeiro non se pode completar con 2x30 pentaminos, xa que a metade das pezas necesita 3 anchas en ambas as direccións. Atopamos una solución de rectángulo 3x20 e non creemos que sexa a única.

Tamén temos outra solución paira a medida 4x15. Paira 5x12 non se atopou ningunha solución. A nosa sesión non foi completa. Por tanto, non podemos dicir que non teña solución. Se Vd. atopase algún, agradeceriámoslle que nolo enviase.

Temos máis información sobre o rectángulo de dimensión 6x10 e podemos afirmar que hai solución e que non é a única; que ademais das simétricas ten moitas solucións (máis de 1.000), como aparece na presentación dunha marca que produce o xogo de pentamino.

Ademais dos rectángulos existen outras figuras que poden formar pentaminos. Imaxes como:

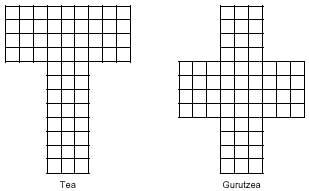
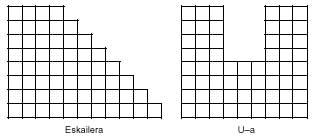
A partir dos pentaminos obtéñense 119 hexaminos, dos que só 35 son diferentes. Se xa é difícil utilizar os 12 pentaminos, pensa en 35 examinos manexando. De todos os xeitos, si es valente, aquí tes 35 hexaminos diferentes:

Tendo en conta que nos 35 hexaminos hai 210 minos, pódense formar rectángulos de dimensións 2x105, 3x70, 5x42, 6x35, 7x30, 10x21 e 14x15. Do mesmo xeito que nos casos anteriores, a primeira non se pode completar con hexaminos. Non sabemos si pódense formar ou non outros. Aí tes o traballo se tes curiosidade. Nos hexaminos da imaxe, cales son os que se poden conseguir encartando o cubo da tridimensión?

Hai outras opcións paira xogar cos poliminos. Una vez máis temos que fuxir dos dominios, triminos e tetraminos, que nos ofrecen poucas posibilidades. Pola contra, os pentaminos e os examinados son adecuados en número de pezas paira o seguinte xogo.

Paira xogar cos pentaminos utilizaremos una táboa de 8x8 cuadraditos (de xadrez) e as medidas dos cadrados serán as do mino.

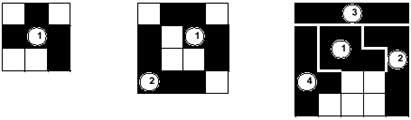
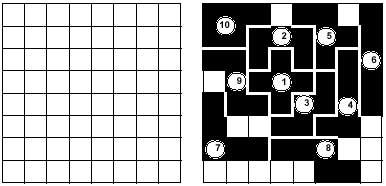
Aínda que o xogo admite moitas modalidades, no fondo non cambia. Os xogadores (dous, tres, catro,...) colocarán as pezas na táboa por quendas. Gañará quen poña o último pentamino. No exemplo da imaxe, o segundo xogador ha gañado o partido, xa que colocou o último pentamino (10). Os 12 pentaminos poderían repartirse aleatoriamente entre os xogadores, ou ben outra posibilidade é que os xogadores poidan elixir as pezas do mesma chea. Tamén se pode xogar por parellas de dúas maneiras.

Tamén se poderían modificar as dimensións do taboleiro. A talla máis pequena é 3x3, xa que algunhas pezas así o requiren. Na táboa 3x3 o xogo non ten fondo, xa que o primeiro xogador sempre gana, xa que nela só se inclúe un pentamino. Na táboa 4x4, pola contra, sempre gañará o segundo xogador. Con isto queremos dicir que aínda que o primeiro xogador elixa a peza que desexe, o segundo sempre terá a opción de colocar a última peza. Ademais, en todos os demais casos a elección do segundo xogador non será única. Deixámosche que inventes este caso especial (o caso do xogador 2 ten una única oportunidade).

Na táboa 5x5 sempre gañará o primeiro xogador si seleccionamos ben a primeira peza. Cal é esa peza?

A partir de agora as posibilidades multiplícanse en táboas de maior dimensión e é difícil realizar unha análise detallada. Por outra banda, o taboleiro non ten cuadrilátero e poderíanse elixir outros tamaños como os rectángulos 5x6, 3x20, 4x15, 5x12 ou 6x10. Na táboa 5x6 hai una xogada adecuada para que o primeiro xogador sempre gañe. Cal é?

Pódese facer o mesmo paira xogar cos hexaminos. O estudo paira este caso converteríase en inacabable, xa que hai 35 pezas. Ademais, ofrece máis posibilidades en canto ao número de pezas. Aí está o rectángulo de 14x15 paira xogar cos hexaminos.