Poliminos (I)

1990/01/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

The word omino comes from the Latin Dominus and means Jaun. However, we will invent another origin: Domino = two minos.

This is a popular 28-piece domino game. The word domino comes from Latin and means Jaun. However, we will invent another origin: Domino = two minos. That is, Domino could mean two minos. Looking at the pieces of the game, you will discover that they are all made up of two paintings. Therefore, following our hypothesis, the word mino would correspond to the square word.

This will be the excuse to build other poliminos from the domino. From now on we will forget the Sunday game and deal with its structure, always under the hypothesis that "mino = square".

Adding two minos you get one piece. The piece seems to be unique even if they are added in any way. We will call this piece domino and the unique being in shape does not give much play.

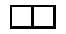
Before moving forward, we warn you that the pieces obtained through all possible symmetries (in the plane) and twists (in the plane and in space) are equal. We will then set an example for you to understand easily.

We approach the construction of triminos. To do this we add one more mino to the domino, obtaining two different triminos:

Triminos don't give us much play either. However, with these two pieces you can make several figures, as seen below:

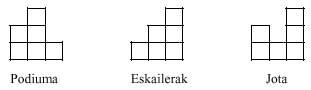
However, it is not possible to make a 2x3 rectangle, as you can easily check.

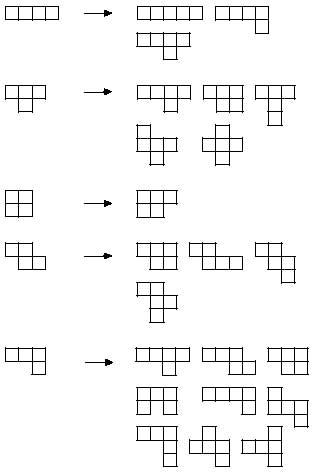
We can pass, therefore, to the next, the tetraminos. For the formation of the tetraminos, we will retain the trimino anyway:

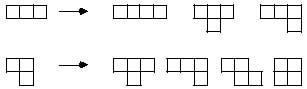
Subtracting them are obtained five different tetraminos:

The five tetraminos collect a total of 20 minos. With them, rectangles of 2x10 and 4x5 can be made. However, none of the five tetramines can be completed. On the contrary, if five pieces can be made the following images:

Let's move forward forming pentamines. Again we take the tetraminos with a mino, anyway:

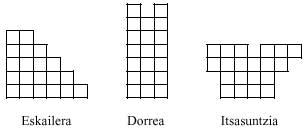
Selecting only different, you get 12 pentamines:

Let us now look at the example initially promised:

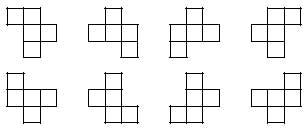
We consider all the pieces that appear in the image as equal.

With 12 pentamines 60 minos are collected that allow to realize rectangles of 2x30, 3x20, 4x15, 5x12 and 6x10. It is clear that the first one cannot be completed with 2x30 pentamines, since half of the pieces need 3 wide in both directions. We found a 3x20 rectangle solution and we don't think it's the only one.

We also have another solution for 4x15 measurement. No solution found for 5x12. Our session has not been complete. Therefore, we cannot say that it has no solution. If you are We would thank him for sending it to us.

We have more information about the rectangle of dimension 6x10 and we can affirm that there is solution and that it is not the only one; that in addition to the symmetrical has many solutions (more than 1,000), as appears in the presentation of a brand that produces the game of pentamino.

In addition to the rectangles there are other figures that can form pentamines. Images such as:

From pentamines 119 hexamines are obtained, of which only 35 are different. If it is already difficult to use the 12 pentamines, think of 35 examines driving. Anyway, if you are brave, here are 35 different hexaminos:

Considering that in the 35 hexamines there are 210 minos, rectangles of dimensions 2x105, 3x70, 5x42, 6x35, 7x30, 10x21 and 14x15 can be formed. As in previous cases, the first cannot be completed with hexamines. We do not know whether or not others can be formed. There you have the job if you are curious. In the image hexamines, what can be achieved by folding the tridimensional cube?

There are other options to play with the miners. Once again we have to flee domains, triminos and tetraminos, which offer us few possibilities. On the contrary, pentamines and examiners are suitable in number of pieces for the next game.

To play with the pentamines we will use a table of 8x8 squares (chess) and the measures of the squares will be those of the mino.

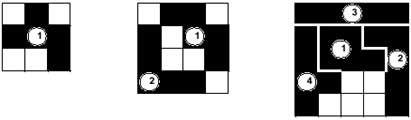
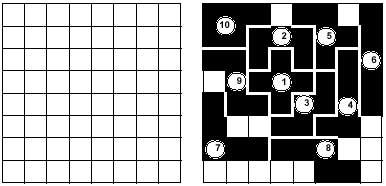
Although the game supports many modalities, in the background it does not change. Players (two, three, four,...) will place the pieces in the table in turns. Whoever puts the last pentamino will win. In the example of the image, the second player has won the match, since he has placed the last pentamino (10). The 12 pentamines could be distributed randomly among the players, or another possibility is that the players can choose the pieces of the same stack. You can also play by pairs in two ways.

The dimensions of the board could also be modified. The smaller size is 3x3, as some parts require it. In the 3x3 table the game has no background, since the first player always wins, since it only includes a pentamino. In the 4x4 table, on the contrary, the second player will always win. With this we mean that even if the first player chooses the piece they want, the second will always have the option to place the last piece. In addition, in all other cases the choice of the second player will not be unique. We let you invent this special case (player 2's case has only one chance).

In table 5x5 the first player will always win if we select the first piece well. What is that piece?

From now on the possibilities are multiplied in larger tables and it is difficult to perform a detailed analysis. On the other hand, the board has no quadrilateral and other sizes such as 5x6, 3x20, 4x15, 5x12 or 6x10 rectangles could be chosen. In table 5x6 there is a suitable move for the first player to always win. What is it?

The same can be done to play with Hexamines. The study for this case would become endless, as there are 35 pieces. In addition, it offers more possibilities in terms of the number of pieces. There is the rectangle of 14x15 to play with the Hexamines.