pi, constante circular

2001/05/01 Roa Zubia, Guillermo - Elhuyar Zientzia Iturria: Elhuyar aldizkaria

• Matematika

El matemático William Oughtred era un hombre pequeño, de ojo negro. Acostaba muy tarde, normalmente dormía intentando resolver algún problema. Cuando circulaba por la calle, la cabeza trabajaba y de vez en cuando paraba y dibujaba en el polvo del suelo los diagramas matemáticos. En 1647 se le ocurrió que para realizar algunos cálculos de círculos se utilizara la letra griega.

Oughtred no utilizó en la relación entre el diámetro y la circunferencia en cambio. Pero así se conoce hoy en día y sería un trabajo inútil cambiar eso. La propia constante matemática es más antigua que la expresión. Lo que sabemos es que desde que el ser humano se preocupó de las matemáticas, hemos conocido el número en. Y es que, comenzando por los babilonios, los geometristas han querido medir su valor exacto.

En la actualidad se ha asignado esta función a ordenadores gigantes. Sin embargo, la reputación del número© se ha extendido fuera del ambiente matemático.

Esta constante se ha utilizado durante 2.500 años, muchas veces sin valor específico. En la Biblia, el primer libro de los Reyes y el segundo de las Crónicas, se describe la construcción del templo de Salomón. Entre otras, se ofrecen medidas concretas del gran depósito de agua denominado Mar de Bronce, de 10 brazos de diámetro y de 30 brazos de cuerda (o perímetro). De esta descripción se deduce que el número amarre amparado por el amante de la memoria daba el valor "3". Otros pueblos le dieron un valor más concreto. Los egipcios y algunas culturas mesopotámicas le otorgaban valores de 3,125 y 3,162, respectivamente. Estos valores pueden asociarse con 25/8 y 10 operaciones.

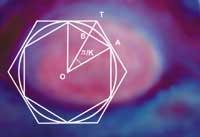
Sin embargo, los griegos Arquímedes de Siracusa (a.C.) 287-212) nos dejó el primer método escrito para el calco teórico del n. Se trata de un cálculo sobre una circunferencia de radio determinado. Por un lado, inscribió en el interior de la circunferencia un polígono regular y, por otro, lo circunscribió dentro de otro polígono mayor de igual número de lados. Al aumentar el número de lados de los polígonos, al aproximarse al infinito, los perímetros exteriores e interiores son iguales, la longitud de la circunferencia.

Con la aplicación de este método, Arquímedes no sacó ningún valor concreto, pero logró una buena aproximación. Alcanzó el polígono de la zona 96 y determinó que el número en g debía estar comprendido entre los valores 223/71 y 22/7 (entre 3,1408 y 3,1429 aproximadamente). La media entre ambos es de 3,1418, que difiere 0,0002 del valor actualmente conocido.

Es un esfuerzo reseñable, ya que Arquímedes no disponía de nuestra notación matemática actual ni de herramientas avanzadas. Otros llevaron la misma metodología más adelante. El dominio de la ciencia se movió poco a poco hacia el este. La siguiente aportación teórica llegó de la mano del matemático Tsu Ch'ung Chi (430-501). Seguramente no conocía Arquímedes. Sin embargo, el resultado de las estimaciones fue de 3,1416, valor que consideramos válido para muchas operaciones.

En Occidente

Próximas referencias europeas XVII. dependientes. El más conocido de esta época es el propuesto por el matemático escocés James Gregory (1638-1675) (aunque a veces el matemático Gottfried Wilhelm von Leibniz sea considerado autor):

6.5/4 = 1 - 1/3 + 1/5 - 1/7 + …

Se trataba de metodologías de origen geométrico, pero con un marcado carácter matemático moderno. No obstante, a medida que se añaden los términos el error aumenta considerablemente. Con fórmulas similares, algunas matemáticas introdujeron muchas horas en el cálculo de los decimales del número©. El matemático inglés William Shanks (1812-1882) obtuvo 707 decimales, de los cuales sólo 527 eran correctos.

El alemán Carl Louis Ferdinand von Lindemann (1852-1939) demostró que también es trascendente, es decir, que no es la solución de un polinomio con números enteros.

Época de los circuitos

XX. A mediados del siglo XX se introdujeron los ordenadores en la historia del número©. F. El inglés Ferguson calculó 808 decimales en 1947 mediante un programa informático. Dos años después llegó a los 2.000 decimales. A partir de ahí, tanto los algoritmos como las calculadoras (ordenadores) han mejorado mucho y, por tanto, el conocido número de decimales ha aumentado considerablemente. Por ejemplo, los matemáticos David Bailey, Peter Borwein y Simon Plouffe, sin necesidad de decimales anteriores, desarrollaron la fórmula para calcular cualquier decimal.

En 1999 eran 68.719.470.000 decimales, pero la competencia continúa. En este sentido, los matemáticos plantean cuestiones casi filosóficas. ¿Cuántas veces aparece una cifra? ¿Hay grandes secuencias repetitivas? ¿Cuál es realmente la naturaleza del número en...?

La verdad de la mentira estadística

XVIII. El matemático francés Georges Buffon del siglo XX descubrió el teorema binomial. Este matemático, sin embargo, se recuerda por el método de cálculo estadístico del n. ¡Curioso! A modo de parrilla dibujó líneas en el suelo y además aleatoriamente lanzó palitos de la mitad de la distancia entre filas. Contaba un punto cada vez que queda cruzado sobre la línea. Dividiendo el número de puntos de 25 tiros por 100 permite una aproximación al n. Con este método, Lazzerini obtuvo en 1901 3.1415929 resultados.