Changement de base

1989/09/01 Arrojeria, Eustakio - Elhuyar Zientziaren Komunikazioa | Lizaso, Pili - Informatika SailaElhuyar Fundazioa Iturria: Elhuyar aldizkaria

• Programazioa

Sous prétexte que nous étions dans le dernier numéro en été, nous vous avons offert un jeu. Bien sûr, vous aurez joué suffisamment et à la fin de l'été, nous devons revenir sur la voie. Nous sommes au début d'un nouveau cours et il est temps de commencer à démarrer les moteurs. Nous espérons que le programme de ce numéro vous aidera dans ce travail.

Le système normal utilisé pour représenter les nombres est l'harmatique, c'est-à-dire un système composé de dix signes ou chiffres différents (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). De toute façon, vous saurez que les ordinateurs travaillent sur le système binaire, c'est-à-dire sur le système à 0 et 1 chiffres, de sorte que pour pouvoir traiter les données saisies par nous doit passer d'une base à l'autre et la même chose, mais vice versa, pour présenter à l'utilisateur les résultats obtenus.

Ce que nous avons voulu analyser dans ce programme a été: les changements de base.

Nous avons pris comme exemple les bases 10, 2 et 16, qui sont les plus utilisées à notre avis.

Conversion de base 10 à base n

Supposons que nous voulions convertir à la base n un nombre qui est à la base 10. Nous divisons le nombre décimal par n et gardons les restes de ces divisions jusqu'à ce que le rapport soit 0.

Ex. : Si nous voulons convertir le nombre décimal 408 à la base 2:

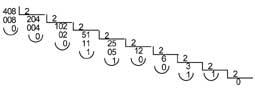
Le numéro 408 dans la base 2 sera 110011000.

Ex. : Conversion du nombre décimal 420 à la base 16

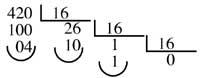
1A4 sera le nombre 420 à la base 16.

Remarque: Le système décimal emploie 10 chiffres et le binaire 2. Par conséquent, l'hexadécimal doit avoir 16 chiffres ou symboles. Comme il n'y a que 10 chiffres décimaux, les 6 premiers caractères de l'alphabet sont utilisés comme chiffres.

Conversion de base n à base 10

Supposons que nous voulions passer un numéro à la base n (a1 a2 ... à la base 10.

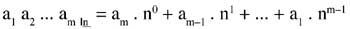
Nous devons le faire.

Il ne peut pas être fait directement pour convertir le nombre m-tar en n-tar sans passer par la base 10. Le nombre m doit devenir décimal puis n-tar le nombre décimal.

Cependant, pour convertir les nombres binaires en hexadécimaux, nous avons un chemin plus simple que pour le cas général. Pourquoi cela ? Car les quatre chiffres binaires forment un nombre hexadécimal. Par conséquent, prendre les chiffres binaires de droite à gauche, si dans le groupe de gauche il manque chiffre en ajoutant les 0 à gauche, et en suivant le tableau ci-joint il suffit de convertir directement à seize.

Parties du programme:

• 10-130: Présentation du menu principal et sélection d'une option.
• 140-200: Définir le nombre d'exercices que vous souhaitez effectuer dans une session.
• 250-550: Résolution d'un ensemble d'exercices.
  • 270: 270 Un nombre décimal est tiré au hasard.
  • 290-330: Le nombre décimal passe à la base 2.
  • 340-400: Le nombre décimal passe à la base 16.
  • 410-430: La base sur laquelle les questions ou les entrées et les résultats doivent être présents est définie.
  • 450-530: Vérification du résultat.
• 610-640: Action d'écrire lentement les chaînes de caractères vers la droite.
• 660-690: Action d'écrire les chaînes de caractères vers la gauche.
• 710-730: Données du programme.

(Note: Pour bien voir l'image aller au pdf).