Musique, hasard ou sagesse ?

1992/01/01 Abajo, Javier | Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Introduction

La musique, celle des jeux des basques, nous ne la découvrirons pas ici. Notre objectif n'est pas d'inventer quelque chose de nouveau. Mais nous essayerons de faire une petite analyse mathématique (probabiliste). Comme dans tous les jeux de hasard, le hasard a beaucoup d'influence, mais si le jeu est correct, nous devons tous être la même chance. Par conséquent, en dehors du hasard, la connaissance et l'expérience sont très précieuses.

Les chances des paires et des points pour cet article, à la fois sur quatre et huit rois, nous les avons calculées et nous nous appuierons sur eux. Les cotes unitaires des quatre joueurs n'ont pas été prises en compte, ni les cotes des cas après le mus. Par conséquent, l'étude sera très superficielle.

Figure . Quatre rois.

Règlementation des normes

Quatre joueurs entrecoupés en deux couples.
Quatre cartes sont distribuées.
L'ordre des lettres va de un au roi.
Quatre sections: grand, petit, paires et jeu (ou point), sont jouées séparément:

• grand: les plus grandes cartes (rois, chevaux, casquettes...)
• petite: cartes inférieures (une, deux, trois,...)
• paires : cartes égales paires deux cartes égales moyennes trois cartes égales duas ou quatre cartes égales
• Jeu : les valeurs des cartes sont ajoutées au point : Priorité 30 ou moins: Jeu 30, 29, 28... Plus de 30 priorité: 31, 32, 40, 37, 36, 35, 34, 33 a) Une fois les cartes distribuées, les joueurs doivent dire s'il y a des
  
  mus
  ou non de la main. b) En cas de mus, les joueurs peuvent enregistrer les cartes qu'ils souhaitent et modifier au moins une d'entre elles. De nouveau au point
  a). c) S'il n'y a pas de musique, les cartes ne peuvent pas être modifiées. d) Le système de pari
  en quatre parties est le même: les joueurs peuvent sauter ou passer (en gardant l'ordre); si un couple frappe envoyer, l'autre aura trois options:

avoir (nahi), dans ce cas à la fin de la main vous verrez qui
gagne; ne pas avoir (ne pas vouloir), dans ce cas le couple qui a frappé l'envoi prendra un
point; toucher plus, monter le pari. Dans ce cas, l'autre partenaire peut choisir entre avoir, ne pas avoir ou toucher plus. A cette occasion, si nous avons le dernier pari, à la fin de la main vous verrez qui est le gagnant, ou si un couple revient (ne l'a pas), l'autre recevra tous les points du pari jusqu'alors.

e) L'envoi est de deux points. Le pari peut être aussi grand que vous voulez, mais tout le jeu est joué là pour parier.
f) Avant de frapper le mur et le jeu, vous devez savoir s'ils ont un partenaire ou jeu. Pour pouvoir frapper l'envoi, il est nécessaire qu'au moins un joueur de couples différents ait un partenaire ou un jeu. Si les quatre joueurs ne jouent pas, vous jouez à des points.
g) Si vous passez au plus grand, au plus petit et au point le cas échéant, le gagnant final recevra un point. Si nous passons au mur et au jeu n'est pas pointé. Cependant, le couple avec le meilleur partenaire ou jeu reçoit des points:

par paires =
1 moyenne = 2
duples = 3

jeux 31 points = 3
repos = 2

Si un couple frappe le point par envoi et que l'autre ne l'a pas, le premier prend un et deux points.

h) Les coups sont joués à 40 points (parfois à 30
points). i) Dans ces règles se trouvent quatre rois et quatre rois. Cependant, il ya une autre alternative à jouer, avec les deux par un et les trois par le roi, c'est à dire avec huit rois et huit par un (un et deux), quatre, cinq, six et sept, casquettes, chevaux et rois (rois et trois).

Figure . A huit rois.

Dictionnaire

Comme tous les jeux, la musique a son propre vocabulaire. Voici la base.

Quand les cartes sont distribuées, décidez s'il y a de la musique ou non :

Esku : à droite du joueur qui a distribué les cartes.
Dessert: partage de cartes.
Mus: le joueur veut changer plusieurs cartes.
Pas de musique: le joueur ne veut pas changer ses cartes.
Avec la main: le couple de la main correspond à la main. Cela signifie généralement qu'il y a mus.
Regardez: le couple de dessert passe la décision au poster (mus ou non).

Sans musique:

Étape, donc, le joueur ne parie pas.
Envoyer: 2 points de pari. Plus
d'envoi, 7 plus : au pari précédent le joueur ajoute 2, 7 plus.
Hordago: le joueur mise toute la main.
Si accepté, il est vu à l'heure actuelle.
Izan, nahi: le joueur accepte le pari, il verra à la fin de la main.
Je ne veux pas: le joueur n'accepte pas le pari.

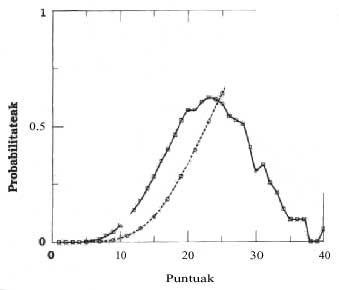
Les figures 1 et 2 montrent les probabilités des points à quatre et huit rois respectivement.

Le point le plus probable pour les quatre rois est 23 avec une probabilité de 0.623, diminuant les chances des deux côtés (ligne continue). Le point 31 est évident, où la probabilité monte un peu, puis descend. La probabilité du point 31 est 0,033.

Dans la figure 1, vous pouvez voir aussi la ligne discontinue. Cette ligne discontinue explique les probabilités accumulées. Par exemple, la probabilité d'avoir 23 ou moins de points est de 0,520. Cette ligne nous dit que la probabilité d'avoir 30 points ou moins est de 0,871, ou la même chose, la probabilité de jouer est de 0,128.

Dans la deuxième image, concernant les huit rois, la ligne continue change radicalement. Le point culminant, par le changement et par son importance dans le jeu, est la probabilité du point 31, étant dans ce cas le plus grand 0,091. L'autre changement significatif est celui de 22 points, dont la probabilité est de 0,086. Dans le jeu, la probabilité du point 40 augmente considérablement.

La ligne discontinue, dans ce cas, nous dit que la probabilité de ne pas jouer est 0, 732 et que la probabilité d'être est de 0,267.

Description des tables

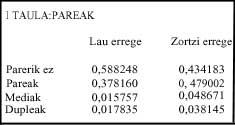
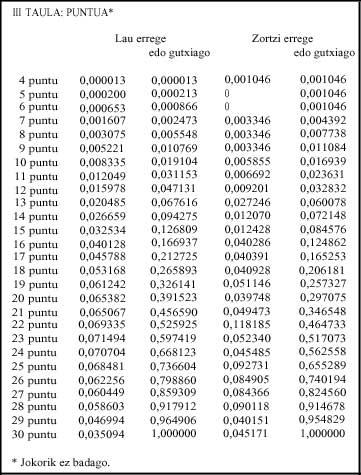
1. Tableau : Le tableau suivant montre la probabilité de chaque type de paire dans quatre ou huit rois. Les cas sont indépendants, c'est à dire, si un joueur a des moyennes, si elle a une paire d'entre eux, nous ne le prendrons en moyenne. La même chose si vous avez duples.
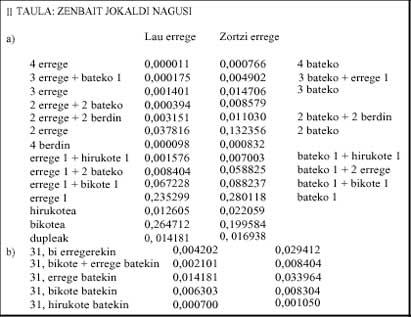
2. Tableau: cette fois, nous pouvons voir les chances de certaines des principales parties. Ces cas sont également indépendants. Par exemple, dans le cas de deux rois n'est pas inclus le cas de deux rois et deux as.
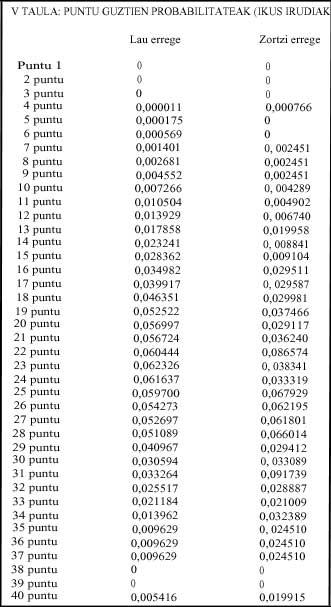
3. Tableau : s'il n'y a pas de jeu, c'est-à-dire que les chances des points apparaissent.
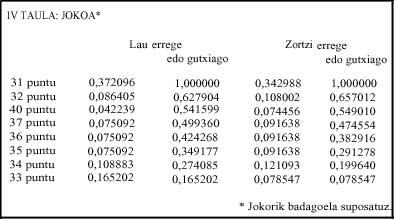
4. Tableau : Considérant qu'il ya jeu, il explique la probabilité de l'égalité de jeu.

Commentaires

La probabilité de ne pas avoir une paire à quatre rois (0,588) est plus grande que celle de l'avoir. L'absence à huit rois (0,434) est moindre (Tableau I).

Notez que dans le mus de huit rois la probabilité des moyennes est supérieure à 0,048 (Table I), dans les deux, 0,038. En revanche, dans le mus de quatre rois est plus grand que celui des duples, 0,017, celui des moyens, 0,015. Cela nous dit que la muse de huit rois est plus directe que l'autre, car le cas le plus probable est évalué.

La probabilité d'un jeu est de 0,128 sur quatre rois et de 0,267 sur huit.

Dans le jeu se produit à l'envers. Dans le mus de huit rois la probabilité de 31 augmente considérablement (0,091) par rapport au carré (0,033). Comme on peut le voir dans la table IIb, les chances de toutes les combinaisons qui se présentent pour obtenir 31 sont mineures dans le mus de quatre rois que dans le zortziko. Par conséquent, nous pourrions dire que la musique de quatre rois est plus directe.

A quatre rois, si tous les joueurs ont moins de 31 points, c'est-à-dire s'il n'y a pas de jeu, la moitié de la probabilité de gagner le pari est obtenue avec 22 points. P(22 ou moins) = 0,525 (Tableau III).

Dans le jeu, à savoir si au moins un joueur de deux paires a plus de 30 points, la probabilité est supérieure à 31, 0,033; parmi tous les jeux (31, 32, 40, 37, 36, 35, 34, 33) un tiers des probabilités (0,372) (tableau IV). Dans ce cas, la moitié des chances de gagner le pari est dépassée avec 40 points; P(40 ou moins) =0,541.

A huit rois, s'il n'y a pas de jeu, c'est à dire si tous les joueurs ont entre 4 et 30 points, avec 22 points n'atteint pas la moitié de la probabilité de gagner le pari. P(23 ou moins) = 0,517 (tableau III).

En cas de jeu, la plus grande probabilité est de 31, 0,091; 0,342 des jeux. Enfin, la moitié des promesses de gagner le pari est obtenue avec 40 points: P(40 ou moins) = 0,549.

Pour finir, il faut dire que les probabilités n'assurent pas les cas et donc vous ne pouvez pas faire confiance. Cependant, comme l'expérience, ils aident. Nous espérons que vous apprécierez cet article et apprendrez à mieux vous comporter.