Mathematica

1998/04/01 Angulo, Patxi | Lazkano, Elena Iturria: Elhuyar aldizkaria

• Matematika

Paira coñecer algo da historia, digamos que a primeira versión de Mathematica saíu en 1988 paira os computadores Apple Macintosh, pero foi rapidamente desenvolvida paira o seu uso noutras plataformas: IBM PC, Silicon Graphics, Hewlett Paccard, Sun, etc… A segunda versión lanzouse en 1991 e foi a que se utilizou nos computadores até setembro do ano pasado, cando finalizou a terceira versión: Mathematica 3.0. Son basicamente similares. A modificación máis significativa é o conxunto de caracteres utilizados paira expresar expresións matemáticas ( mathematical typesetting ). Os novos símbolos matemáticos teñen un significado tipográfico e funcional. Por exemplo, cada operación tiña o seu código ou clave de palabra en versións anteriores. Nesta última versión, a maioría das operacións pódense expresar tanto por clave de palabra como por escritura matemática. Por exemplo:

Power[2,10] ou 210
Sqrt[28 ] ou “w28

Ao mesmo tempo , os ficheiros creados por Mathematica versión 3.0 son expresións propias de Mathematica, o que permite manipulalos en programas como calquera outra expresión simbólica. A capacidade de computación tamén é maior nesta versión, con maior velocidade de execución e menor memoria nalgunhas operacións. Tamén se incorporaron novas funcións e ferramentas, e melloráronse outras xa coñecidas. Mencionar tamén que é necesario dispor dun computador simpático suficiente paira utilizar esta última versión de forma cómoda, xa que recomendan 16 MB de Ram e 75 MB de disco duro. Paira finalizar, indicar que todos os exemplos que se van a expor serán realizados con Mathematica versión 3.0.

A súa principal vantaxe é a súa capacidade paira traballar con expresións simbólicas. “Calquera cousa pode expresarse como simbólica expresiva”. Esa foi a idea básica dos que construíron Mathematica. Por tanto, pode utilizarse como calculadora numérica ou simbólica, serve paira visualizar datos e funcións, ofrece unha linguaxe de alto nivel paira escribir programas, é unha contorna idónea paira a análise de datos e, sobre todo, é una ferramenta capaz de combinar texto, gráficos (si deséxase animados) e fórmulas activas en documentos interactivos. Tamén pode manexar o son, xa que permite definir obxectos de son.

Mathematica pode realizar tres tipos de operacións: numéricas, simbólicas e gráficas. En canto á computación numérica, a forma máis sinxela de utilizar Mathematica é utilizala como calculadora. Con todo, as calculadoras teñen una precisión fixa, é dicir, o número de cifras decimais está fixado de antemán, mentres que en Mathematica pódese indicar na propia orde a precisión requirida ao cálculo. No seguinte exemplo os que están en negrita son os pedidos realizados a Mathematica e en letra simple as respostas dadas por Mathematica (as palabras crave In:=[número] e Out=[número] que aparecen anteriormente son engadidas polo propio programa paira diferenciar as entradas e saídas, relacionar cada saída coa entrada correspondente e despois facer referencias a ditas entradas/saídas mediante un número sinxelo).

l n[1]:=log[4Pi]
Out[1]=log(4cer)
l[2]:=n[Log[4ler]] Out[2]=2.53102
ln[3]:=n[Log
4cer],10]
Out[3]=2.531024247

Por outra banda, o conxunto de operacións é maior, unhas 750 funcións de integral elíptica e Bessel, incluíndo a factorización de funcións hipergeométricas e números enteiros.

Tamén pode aplicar operacións numéricas como integración numérica, programación lineal, etc. Ademais, proporciona solucións a ecuacións algebraicas e a ecuacións diferenciais convencionais.

Entre as computaciones simbólicas que realiza destaca a manipulación de fórmulas algebraicas. O polinomio e a expresión racional poden simplificarse, estenderse ou factorizarse. Tamén pode atopar solucións algebraicas de ecuacións polinomiales e sistemas de ecuacións. A diferenza da segunda versión, na última versión incorpora facilidades paira traballar con matrices e non é obrigatorio o uso de táboas paira a definición de matrices.

Así mesmo, avalía simbólicamente as integrais e os seus derivados, manexando aproximacións por series e calculando límites.

No campo dos gráficos, realiza gráficos bidimensionales e tridimensionales, plots densidade e contour (visións superiores), tanto desde funcións como desde listas de datos. Ademais, existen numerosas posibilidades de controlar os detalles do gráfico, p.ex. : enfoque, cor, luminosidade…

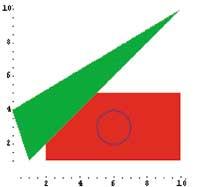
Dispón dunha biblioteca paira gráficos predefinidos, que mediante unha serie de ordes primitivas de obxectos xeométricos (por exemplo, polígonos) mostra os obxectos gráficamente mediante unha representación simbólica.

} rectángulo


=

Graphics[{RGBColor[1,0,0], Rectangle[{2,1}, 10, 5}] rectángulo
=




Graphics[{RGBCcolor[1,0,0], Angle[{2,1}, {10, 5}]>
Graphics

•Graphics•

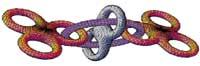
Todos os gráficos formados por Mathematica teñen formato PostScript (PS) polo que poden ser transportados a outras aplicacións.

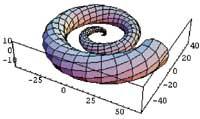
ParametricPlot3D[{uCos[ou] (4+Cos[v+ou]),
uSin[ou] (4+Cos[v+ou]), uSin[v+ou]}, {ou,0,4>}, {v,0,2>}, PlotPoints > {60,12}]

Ademais, ten unha linguaxe propia, polo que se poden escribir programas na linguaxe Mathematica.

Por outra banda, a linguaxe de programación Mathematica admite diferentes estilos de programación: procedimental, con estrutura de bloques, ordes condicionais e flejes repetitivos; funcional, con axentes funcionais; programación baseada en regras, equiparación modal ( pattern matching ) e programación orientada a obxectos.

O programa Mathematica estrutúrase en dous grandes partes: o kernel e o front-end. Kernel é o núcleo, a parte encargada de realizar os cálculos, e o front-end é só a parte que interacciona co usuario, una interfaz cómoda paira o usuario e cuxas ordes son enviadas ao kernel. Se o kernel é o mesmo en todas as plataformas de computador, poderiamos atopalo con diferentes front-end, que se optimizou paira certas arquitecturas. Este front-end ofrece ao usuario documentos denominados “notebook”, é dicir, texto graduado por prioridade, gráficos animados e expresións matemáticas (fórmulas, etc.) Cadernos que admite. Nestes cadernos pódese elaborar material pedagóxico ou doutro tipo, e a característica máis singular é que, ademais das explicacións escritas, pódense realizar operacións nos mesmos.

En xeral, Mathematica caracterízase pola súa compatibilidade comunicativa con outros moitos programas. Isto permítelle ler datos en diferentes formatos (C, Fortran, TEX). Ao utilizar o estándar MathLink, pode intercambiar datos e comandos con outras aplicacións.

Durante a execución do mathematica cárganse algunhas bibliotecas estardíes. Nelas inclúense funcións básicas de cálculo matemático, gráficos e outras áreas matemáticas comúns. Con todo, Mathematica tamén dispón doutras bibliotecas máis específicas que non se cargan cando se inicia o programa. A carga dos mesmos ou dos Packages definidos paira as súas necesidades específicas está a disposición do usuario. Por exemplo, supoñamos que definimos as funcións “factorial” e “exponencial” na libraría “gurelib”.

DeclarePackage[“Calculus`gurelib`”,{”factorial”,”exponencial”}]

una vez executada a orde, poderemos utilizar as operacións factorial e exponencial segundo a norma de orde dada na definición. A biblioteca que Mathematica ten cargada en cada momento se garda na variable global $Packages.

Como non podía ser doutra maneira, Mathematica tamén ten a súa propia dirección Web, onde se poden atopar información, gráficos e últimas noticias: http://www.wolfram.com