Mathematica (III)

1998/06/01 Angulo, Patxi | Lazkano, Elena Iturria: Elhuyar aldizkaria

• Matematika

3. Extremos condicionados dunha función

• Enunciado

Moitas veces, ao calcular os extremos dunha función, dannos as condicións que deben cumprir eses extremos. É dicir, só teremos que aceptar algúns resultados. No exemplo seguinte veremos como se poden calcular os extremos condicionados dunha función mediante Mathematica.

• Pasos da resolución

Primeiro calcularemos os extremos normais da función paira logo poder comparalos cos extremos condicionados. Calcularemos os extremos condicionados utilizando o método de multiplicadores de Lagrange.

• Ordes a utilizar

D: calcula a derivada dunha función respecto da variable dada.

Solve: é a orde de resolución de ecuacións.

Unión: fai a recompilación de listas eliminando elementos repetidos.

/ : aplica a regra ou conxunto de regras que se indica á dereita á expresión esquerda.

Plot3D: fai una imaxe tridimensional dunha función.

ViewPoint: mostra a imaxe tridimensional desde un punto de vista concreto.

AspecRatio: representa a proporción entre os eixos do gráfico.

DisplayFunction: permite visualizar o gráfico ou non.

PlotRange: permite limitar os valores da función no gráfico.

Axes: característica de representar ou non os eixos dos gráficos.

Boxed: representa a caixa en imaxes tridimensionales.

RGBColor: serve paira seleccionar a cor da imaxe dun gráfico.

Point Size: indica o tamaño que terá o punto na imaxe.

Point: adapta as bandas de dúas ou tres elementos a un plano ou punto do espazo.

Show: mostra os compoñentes gráficos.

ParametricPlot3D: realiza un gráfico tridimensional a partir de ecuacións paramétricas. Utilízase paira representar superficies que non poden expresarse como funcións.

Box Cocientes: permite expresar as proporcións entre os eixos dos gráficos tridimensionales.

Contour Plot: representa as curvas de nivel dunha imaxe tridimensional.

ParametricPlot: grafico bidimensional a partir de ecuacións paramétricas. Utilízase paira representar curvas que non se poden representar como funcións.

PlotStyle: permite definir algunhas características da imaxe.

Graphics: converte o dato que se lle dá nun elemento representable.

Polygon: une os puntos outorgados mediante un polígono.

• Resolución por Mathematica

g[x_, e_]:= y3 + ^x2 e + ^2x2 + 2y2 - ^4e – 8

Extremos comúns:

d1[x_,e_]:=D[g[x,e],x]d2[x_,e_]:=D[g[x,e],e]

punegon=Solve[{d1[x,e]==0,d2[x,e]==0},{x,e}]punegon=Union[punegon]

{{X B 0, e Regra -2}, {x Regra 0, e Regra -2}, {x B 0, e
B 2},{x B 0, e
B/3}{{x B 0, e -2}, {x 0, e B/3}}

d11[x_,e_]:=D[g[x,e],{x,2}]d22[x_,e_]:=D[g[x,e],{e,2}]d12[x_,e_]:=D[g[x,e],x,e]

h1[x_,e_]:=d11[x,e]h2[x_,e_]:=d11[x,e]d22[x,e]-d12[x,e]2

hess={1,h1[x,e],h2[x,e]}
hess / punk

{1, 4 + 2 e, -4 x2 + (4 + 2e) (4 + 6e)}{{1,
0, 0}, {1, 16/3, 128/3}

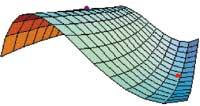
No primeiro punto (0,-2), este método non nos di o que pasa porque hai temas da serie que son cero. Por tanto, non podemos decidir a natureza deste punto. No segundo punto (0,2/3), en cambio, a función ten un mínimo relativo xa que todos os temas da sucesión de barreiras son positivos.

p0=Plot3D[g[x,e], {x,-1,1}, {e,-3,1}, ViewPoint} {1,0.5,0.25}, AspectRatio False Automatic, DisplayFunction Identity, PlotRange> All, Axes False, Bose False]

-Surface Graphics-

mut=Graphics3D[{{RGBColor[0.5.0.0.5], Point[0.03], Point[{0,-2.g[0,-2]}], {RGBColor[1.0,0], Point[0.03], Point[{0,2/3.g[0]+0.1}]

-Graphics3D-

Show[p0, mut, DisplayFunction:>$DisplayFunction]

-Graphics3D-

Extremos condicionados:

Condición x2+y2=1

F[x_,e_]:=g[x,e]+l(x2+y2-1)

d1F[x_,e_]:=D[x,e],x]d2F[x_,e_]:=D[F[x,e],e]d11F[x_,e_]:=D[F[x,e],{x,2}]d22F[x_,e,12_]:

pungel=Solve[{d1F[x,e]==0,d2F[x,e]==0,x2+y2==1}, ^{x,e, l}]

{{l Territorio -(5/2), x Regra 0, e Regra
-1},{l -(3/2), x Regra 0, e Regra 1}

h1F[x_,e_]:=d11F[x,e]h2F[x_,e_]:=d11F[x,e]d22F[x,e]-d12F[x,e]2

hessF={1,h1F[x,e],h2F[x,e]}

{1, 4 + 2e + 2l, -4 x2 ⁺ (4 + 2e + 2l) (4 + 6e + 2l)}

hessF / pungel

{{1,-3,21},{1,3,21}

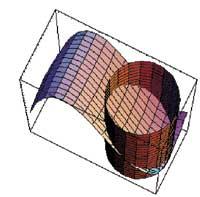
Por tanto, no primeiro punto, (0,-1), ten un mínimo e no segundo, (0,1), o máximo, segundo os signos dos temas da sucesión de valos.

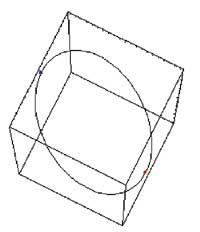
zi=ParametricPlot3D[{Cos[t], Sen[t], z}, {t,0,2>}, {z,-10,0}, Box Cocientes Regula Automatic, DisplayFunction Identity]

-Graphics3D-

p1=Plot3D[g[x,e],{x,-1,1},{e,-3,1}, Box Cocientes Regula Automatic, DisplayFunction Regra Identity]

Show[p1, zi, DisplayFunction:>$DisplayFunction,ViewPoint
B {1,0.5,8}]

-Graphics3D-

ps1=Graphics3D[{{RGBColor[1,0,0], Point[0.025], Point[{0,1,-9}]}, {RGBColor[0,0,1], Point[0.025], Point[{0,-1,-3}]]

-Graphics3D-

mb1=ParametricPlot3D[{Cos[t], Sen[t], -3Sen[t]-6}, {t,0,2{}, ViewPoint
{1,.0.5,8},DisplayFunction> Identity]

-Graphics3D-

Show[mb1, ps1, DisplayFunction:>$DisplayFunction]

-Graphics3D-

kp2=ConcanalPlot[g[x,e], {x,-2.5,2.5}, {e,-3,1},
AspectRatio> Automatic,DisplayFunction Regra
Identity]

-Contour Graphics-

mb2=ParametricPlot[{Cos[t], Sen[t]}, {t,0.2},
PlotStyle> RGBCcolor[0,1,0],

AspectRatio Establecido
Automatic,DisplayFunction Identity]

-Graphics-

ps2=Graphics[{{RGBColor[1,0,0], Point[{0.06], Point[{0,1}]}, {RGBColor[0,0,1], Point Size[0.06], Point[{0,-1}]]

-Graphics-

mut2=Graphics[{{RGBColor[0.5.0.5],Polygon[{-0.025,-2.025},{-0.025,-1.975},{0.025,-1.975},{0.025,-2.025},{-0.025,{-0.025},{-0.025,}

-Graphics-

Show[kp2, mb2, mut2, ps2, DisplayFunction:>$DisplayFunction]

-Graphics-

• Comentarios

En primeiro lugar, calculamos os extremos normais mediante o método tradicional. É dicir, calculamos as primeiras derivadas parciais utilizando a orde D e resolvemos o sistema de ecuacións que se xera igualando con cero a través de Solve. Utilizouse a orde Unión paira eliminar as solucións repetidas do sistema. Por último, coas segundas derivadas parciais completamos a sucesión de barreiras e determinamos os extremos en función da sucesión correspondente a cada punto. Estes extremos son os que se poden distinguir na imaxe realizada coas ordes Plot3D, Graphics3D e Show.

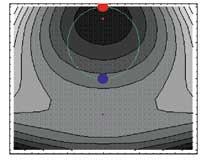
Na segunda parte utilizouse o método de Lagrange paira calcular os extremos condicionados. Paira iso valémonos como antes de as ordes D e Solve. A continuación realizáronse as imaxes tridimensionales de función e condición utilizando Plot3D e ParametricPlot3D. Máis abaixo representouse a curva de intersección entre función e condición e os puntos atopados coas ordes Graphics3D, ParametricPlot3D, Point e Show.

Por último, realizouse una proxección superior de función e condición (Contour Plot) na que se colocaron os extremos normais (Polygon, cadrado) e condicionados (Point, círculo).