Da Terra á Lúa

2001/06/01 Bandres Unanue, Luis Iturria: Elhuyar aldizkaria

• Fisika

Primeiro, analicemos si teoricamente, polo menos, é posible tirar un proxectil cun canón e non caer este a a Terra. A teoría dinos que si. Vexamos as dúas posibilidades extremas. Na primeira delas, o tiro realizarase verticalmente cara arriba e coa Terra soa (nin aire nin calquera outro tipo de fricción) bastará con dotar ao proxectil da enerxía cinética necesaria para que salga da influencia da Terra. No caso de que o cálculo non moi complicado dea ao proxectil una velocidade de 12.386 km/s (ou superior), pódese observar que ocorrerá o devandito.

Outra opción é lanzar o proxectil horizontalmente. Por que en casos normais cae o proxectil á Terra? Porque a terra tira de abaixo. Por iso, o seu percorrido é o da liña que se inclina cara ao chan en lugar de ser rectilíneo e finalmente atópase con el. É certo que a superficie da Terra é curva, pero a inclinación da traxectoria do proxectil é moito máis pechada que a da Terra. Si reducísemos a inclinación da traxectoria do proxectil e fixésemolo tan grande como a superficie da Terra, o proxectil nunca caería á Terra e seguiría virando ao redor dela, converténdose no satélite da Terra. Pero como se pode conseguir? Como antes, dando ao proxectil a velocidade necesaria.

Nel temos a sección dun sector da esfera terrestre. O canón atópase na cima A de un monte. Si a Terra non tivese gravidade algunha, despois dun segundo de tiro horizontal, o proxectil sería no punto B. Pero a forza da gravidade cambia esta situación e, tras un segundo, o proxectil sitúase a cinco metros por baixo do punto B, é dicir, no punto C (calquera corpo que caia libremente sobre a Terra e no baleiro ocupa un percorrido de cinco metros no primeiro segundo). Por tanto, se despois de baixar eses cinco metros o proxectil fóra á mesma altura do punto A de a superficie terrestre, a súa traxectoria sería una curva concéntrica coa superficie da esfera terrestre.

Agora temos que calcular a lonxitude do segmento AB, é dicir, o camiño horizontal que ocupa o proxectil no primeiro segundo, polo que a velocidade que debe ter o proxectil ao saír da boca do canón paira conseguir o noso obxectivo. O cálculo é sinxelo: Tomando o triángulo AOB, este é recto no vértice A. Por outra banda, considerando OA = OC = radio da esfera terrestre, 6.370.000 m aproximadamente, e OB = OC - BC = 6.370.005 m. Disporémolo a través do teorema de Pitágoras, uns 8.000 m.

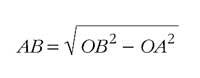
É dicir, se non fose aire (isto ponlle un gran obstáculo a calquera corpo que vaia a velocidade moi alta), calquera proxectil lanzado horizontalmente e a unha velocidade inicial de 8 m/s nunca caería sobre a Terra.

E se a velocidade fose maior, que pasaría? Segundo a mecánica de amasado. O proxectil de 8 km/s a 11,2 km/s cubriría as elipses ao redor da Terra e as elipses serán máis longas a medida que aumenta a velocidade inicial. Pero con esta velocidade de 11,2 km/s, en lugar de ser elipse, teremos una curva aberta, é dicir, una parábola, que abandona a Terra paira sempre.

Por tanto, teoricamente podemos lanzar una bala de canón até a Lúa. Paira iso só hai que darlle una alta velocidade inicial.

Agora imos analizar a viaxe á Lúa en función de Xullo Verne e da realidade. O sucedido tras a lectura de devandita novela. Nese momento sucedeu algo sorprendente: todos os obxectos que estaban dentro do proxectil perderon o seu peso, e os propios viaxeiros, que quedaron suspendidos no aire sen agarrarse a ningunha parede. Pero o autor non tivo en conta que debía suceder o mesmo antes de pasar por este punto e tamén despois, é dicir, que tantos pasaxeiros como obxectos estarían ingravemente desde o mesmo momento en que comezou a viaxe.

Isto parece una desfiguración, pero despois de pensar un pouco, veremos que ten que ser así. Paira darse conta disto tomemos outro episodio da mesma novela de Xullo Verne. Como se lembrará ao lector, os viaxeiros viron que tras arroxar o corpo do can fóra, en lugar de caer este a a Terra, sorprendidos, seguían no espazo xunto co proxector. Vern dá resposta adecuada a este fenómeno con precisión e acerto. É dicir, como sabemos, como no baleiro a Terra dá a mesma aceleración a todos os corpos, todos caen á mesma velocidade. Neste caso, tanto o proxectil como o corpo do can, debido á influencia da Terra, desprazaríanse exactamente igual. Por tanto, a velocidade relativa entre eles será cero, ou o que é o mesmo, o corpo lanzado e os pasaxeiros irían xuntos.

Pero o que Verne non tivo en conta era: se o corpo do can está fóra do proxectil e non cae cara á Terra, por que cae cando está dentro? Se o corpo do can colócase no interior do proxectil (sen ningún tipo de soporte, como cando está fose), cólgase ou queda no espazo, é dicir, a velocidade relativa entre ambos os corpos é cero, polo que se detén un do outro.

Cando un corpo e o seu soporte móvense no espazo coa mesma aceleración, non hai ningunha presión entre eles.

Sen beizos, todo o que dixemos sobre o can ocorre ademais cos corpos, cos pasaxeiros ou con todos os aparellos que están dentro do proxectil e por tanto, aínda que se perdan os puntos de apoio, non caen. É dicir, a cadeira situada sobre o pavimento no interior do proxectil que vai en voo, se se colocase patas para arriba contra o teito, non caerá cara abaixo e continuará contra o teito. Calquera pasaxeiro pode sentar sobre el sen medo a caer ao chan do proxectil (de non ser así a cadeira caería). Pero iso non é posible, porque sabemos que todas as cousas que están dentro do proxectil teñen a súa propia aceleración.

Ao parecer, Jules Verne non se deu conta de que, na súa opinión, dentro do proxectil, en voo libre, os obxectos presionarían nos seus puntos de apoio, como o fan cando o proxectil está parado. É certo que os corpos, cando están sobre unha superficie da zona gravitatoria, presionan sobre ela se o gaizanal está a moverse parado ou a unha velocidade uniforme, pero cando un corpo e o seu soporte móvense no espazo coa mesma aceleración, non se realiza ningunha presión (se as aceleracións son debidas a forzas externas, como é o caso, e non á influencia do motor do proxectil).

Isto significa que, una vez finalizado o efecto dos gases do canón no proxectil, os viaxeiros e demais obxectos interiores perderon o seu peso e permanecerían sen gravidade. Sabendo isto, os viaxeiros podían recoñecelo facilmente no espazo libre ou no interior do canón. Pero o novelista non se deu conta diso e na primeira metade da viaxe sideral cóntanos os quebradizos de cabeza que tiveron os viaxeiros paira saber se voaban ou non:

• Nicholl, estamos a mover?
• Nicholl e Ardan miráronse. Non sentían as vibracións do proxectil.
• Ou estamos tranquilos sobre o chan de Florida? Nicholl preguntou.
• Ou no fondo do golfo de México, engadiu Michele.

Estas condicións poden ser paira os pasaxeiros do barco, pero non paira os proxectís en voo libre. Os primeiros terán o seu peso propio, mentres que os segundos perderían a súa gravidade e serían inmediatamente a conta.

A viaxe deste tipo de proxectil debería ser sorprendente! Un mundo pequeno no que os corpos non pesan e deixarían as cousas libres da man e seguirían nun lugar tranquilo sen caer; os obxectos terían o seu equilibrio en calquera posición e a auga non caería cando a botella tivésese que dobrar...

Desgraciadamente Xullo Verne tivo en conta todas estas cousas que non tiña no seu traballo "Da Terra á Lúa" e perdeu una gran oportunidade. Con todo, a novela é realmente marabillosa, a pesar de ter algún erro físico.