Matemáticas de Leonardo

1992/05/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Leonardo dá Vinci (1452-1519) é o exemplo dos científicos do Renacemento. Este científico, como é coñecido, dedicouse a moitos campos da ciencia: Anatomía, Óptica, Botánica, Bioloxía, Xeografía, Xeoloxía, Mecánica, Xeometría, Pintura, Escultura, Urbanismo, Arquitectura, Astronomía, Náutica, Física, etc. Non había quen non animase a investigar as súas curiosidades. Tiña que explorar todo.

Aínda que é máis coñecido nas artes, non podemos descartar achegas noutros ámbitos. Leonardo foi autodidacta e, a diferenza doutros científicos de entón, non sabía nin latín nin grego. Con todo, isto non significa que as súas obras carezan dunha base sólida. Pola contra, cando se mergullaba nunha obra (ciencia) estudaba en profundidade todas as formas. A súa curiosidade era tan grande que deixaba a miúdo o traballo que estaba a realizar.

Sabemos que cando regresou a Florencia en 1501, tras estar con Luca Pacioli, mergullouse na Xeometría. Mentres tanto , o tímpano do cadro de Santa Ana non parou de facer. Desde 1501 dedicouse á Xeometría; entre 1504 e 1506 á Hidráulica; en 1505 estudou a xeometría dos sólidos nun escribo; en 1510 foi atraído pola Anatomía; etc.

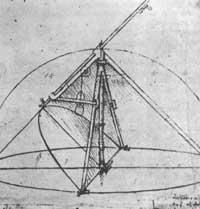
Pero neste artigo queremos mencionar as matemáticas de Leonardo, menos coñecida.

O mozo Leonardo aprendeu moito na escola de Andrea Verrocchio. No taller de Verrocchio estudábase non só a pintura, senón tamén o bronce fundido, a pedra, os planos, a apertura de canles, a construción de casas, etc. En todas estas “artes”, o coñecemento da perspectiva tamén na pintura tiña gran importancia, pedíase una base científica (sobre todo matemática) enorme. A formación de Leonardo era práctica, fundamentalmente Enxeñeiro Leonardo, maquinista, non teórica. Por iso, é da súa xeometría mecánica. As solucións que busca son prácticas (que se poden facer con ferramentas reais) e non teóricas.

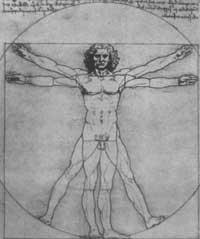
Exemplos desta tendencia práctica son os estudos sobre a construción de polígonos regulares inscritos en círculo. Nos seus escritos aparecen estas imaxes e moitas propiedades. Entre outras cousas, as relativas ao cadro do círculo; a inscrición dos polígonos de 3, 6, 8, 24 (é fácil e Leonardo faio coa apertura constante do compás), una aproximación á construción dos polígonos regulares (como o pentágono e o haptágono que non se poden construír directamente mediante regras e compases, é máis difícil de realizar, pero Leonardo ten suficiente solución próxima).

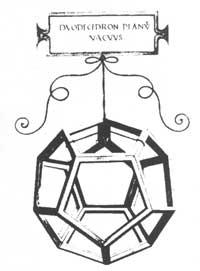
Probablemente serán seus os cheos e baleiros de poliedros regulares e semi-regulares que ilustran o código “Divina Proportione” que Luca Pacioli ofreceu a Ludovico Mairua en 1498. Realiza a dirección do círculo e arroxa un cuadratura, círculo ou rodete sobre una recta ou un plano. Esta solución supón un descoñecemento do problema teórico. Con todo, enténdese desde o punto de vista do enxeñeiro.

Sen dúbida, Leonardo debía a súa sabedoría matemática a Luca Pacioli. E é que o conseguiu axiña que como publicaba Summa e logo reconciliouse co seu autor. Tamén coñeceu a Alberto de Sajonia, Jordanus Nemorarius (a quen moitas veces se refería) e Nicolás de Cusa (que sen dúbida influíu nel). Seguramente non estudou directamente a Arquímedes, pero está claro que o coñeceu indirectamente a través de Eutocio e Giorgio Val.

É raro que non cee de Leonardo Algebra. Era difícil ou demasiado abstracto?. Era, con todo, una xeometría pura que substituía o descoñecemento teórico do espazo polo seu poder visual. As reflexións sobre os conceptos básicos da xeometría son moi interesantes, aínda que a influencia de Aristóteles e Nicolás de Cusa é evidente.

Leonardo non retrocede ante o uso de conceptos infinitesimais (é o paso ao límite). Por exemplo, propón dividir o centro de gravidade do semicírculo en pirámides (triángulos) de determinación, tantas pirámides como sexan necesarias para que a fraxilidade das súas bases sexa inapreciable e case directa. Con todo, leste é un caso excepcional e, en xeral, os métodos de Leonardo son máis simples, correctos e elementais.

As ideas intuitivas, probablemente, leváronlle ao seu maior descubrimento, a calcular o centro de gravidade da pirámide. Parece que trasladando ao espazo o mesmo razoamento que fixo sobre o centro de gravidade do triángulo do plano, pasando polo tetraedro regular, puido situar o seu centro de gravidade no punto de corte dos seus eixos (é dicir, as rectas que unen un vértice co centro de gravidade ao lado oposto) e ao cuarto da distancia da base.

Máis tarde descubriu que as rectas que unen os puntos centrais das esquinas contra un tetraedro córtanse no centro de gravidade. Finalmente, xeneralizou o descubrimento, indicando que o centro de gravidade de calquera pirámide atópase no seu eixo (da base á cuarta parte).

As investigacións sobre a transformación recíproca de sólidos baséanse en “De transmutationibus geometricis” de Nicolás Cusa, quen aplica os métodos de Val paira resolver problemas enunciados polo cusés (formando a confluencia de varios cubos, convertendo un cubo nun prisma e viceversa). Con todo, Leonardo tamén considera transformacións especiais. Por exemplo, entre o cubo e a pirámide.

Leonardo tamén se ocupou das lumulas de Hipócrates. Ademais das numerosas mencións dos seus Cadernos, en 1514 tentou escribir un tratado: De ludo xeométrico, que quedou incompleto como toda a súa obra. Enténdese que exista una certa paixón polo valor estético das lumulas. De paso, en Occidente descubriu unhas proposicións xeométricas que aínda non se coñecían. Por exemplo, estableceu que a suma das superficies das lumulas construídas sobre os lados dos triángulos equiláteros era igual á do triángulo.

Cabe mencionar a enxeñosa solución mecánica que Leonardo atopou paira o problema de Óptica da o-Hazi cun compás especial. Esta solución de Leonardo indica profundos coñecementos sobre as propiedades dos cortes cónicos. Geométricamente 150 anos despois foi resolto por Huygens.

As investigacións sobre perspectiva realizadas por Leonardo publicáronse no “Tratado da pintura” en 1651.

Hai que dicir que a Leonardo débenselle imaxes e proxectos de ferramentas matemáticas, compases de proporción e un parabológrafo que utilizou paira construír espellos parabólicos.

A influencia das matemáticas tamén se pode apreciar nas súas pinturas. Leonardo codificó as proporcións do corpo facendo a xeometría infraestrutura das súas pinturas. A súa composición responde a un esquema armónico facilmente localizable, con estruturas radiais, troncos de cono, triángulos, arcos, espirales, trapecios, pentágonos, etc.