Matemàtiques de Leonardo

1992/05/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Leonardo da Vinci (1452-1519) és l'exemple dels científics del Renaixement. Aquest científic, com és conegut, es va dedicar a molts camps de la ciència: Anatomia, Òptica, Botànica, Biologia, Geografia, Geologia, Mecànica, Geometria, Pintura, Escultura, Urbanisme, Arquitectura, Astronomia, Nàutica, Física, etc. No hi havia qui no animés a investigar les seves curiositats. Havia d'explorar tot.

Encara que és més conegut en les arts, no podem descartar aportacions en altres àmbits. Leonardo va ser autodidacta i, a diferència d'altres científics de llavors, no sabia ni llatí ni grec. Tanmateix, això no significa que les seves obres manquin d'una base sòlida. Per contra, quan se submergia en una obra (ciència) estudiava en profunditat totes les formes. La seva curiositat era tan gran que deixava sovint el treball que estava realitzant.

Sabem que quan va tornar a Florència en 1501, després d'estar amb Lucca Pacioli, es va submergir en la Geometria. Mentrestant , el timpà del quadre de Santa Ana no va parar de fer. Des de 1501 es va dedicar a la Geometria; entre 1504 i 1506 a la Hidràulica; en 1505 va estudiar la geometria dels sòlids en un escric; en 1510 va ser atret per l'Anatomia; etc.

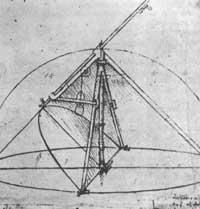
Però en aquest article volem esmentar les matemàtiques de Leonardo, menys coneguda.

El jove Leonardo va aprendre molt a l'escola d'Andrea Verrocchio. En el taller de Verrocchio s'estudiava no sols la pintura, sinó també el bronze fos, la pedra, els plans, l'obertura de canals, la construcció de cases, etc. En totes aquestes “arts”, el coneixement de la perspectiva també en la pintura tenia gran importància, es demanava una base científica (sobretot matemàtica) enorme. La formació de Leonardo era pràctica, fonamentalment Enginyer Leonardo, maquinista, no teòrica. Per això, és de la seva geometria mecànica. Les solucions que cerca són pràctiques (que es poden fer amb eines reals) i no teòriques.

Exemples d'aquesta tendència pràctica són els estudis sobre la construcció de polígons regulars inscrits en cercle. En els seus escrits apareixen aquestes imatges i moltes propietats. Entre altres coses, les relatives al quadre del cercle; la inscripció dels polígons de 3, 6, 8, 24 (és fàcil i Leonardo ho fa amb l'obertura constant del compàs), una aproximació a la construcció dels polígons regulars (com el pentàgon i l'haptágono que no es poden construir directament mitjançant regles i compassos, és més difícil de realitzar, però Leonardo té suficient solució pròxima).

Probablement seran seus els plens i buits de poliedres regulars i semi-regulars que il·lustren el codi “Divina Proportione” que Lucca Pacioli va oferir a Ludovico Mairua en 1498. Realitza la direcció del cercle i llança un quadratura, cercle o corró sobre una recta o un pla. Aquesta solució suposa un desconeixement del problema teòric. No obstant això, s'entén des del punt de vista de l'enginyer.

Sens dubte, Leonardo devia la seva saviesa matemàtica a Lucca Pacioli. I és que ho va aconseguir tan aviat com publicava Summa i després es va reconciliar amb el seu autor. També va conèixer a Alberto de Saxònia, Jordanus Nemorarius (a qui moltes vegades es referia) i Nicolás de Cusa (que sens dubte va influir en ell). Segurament no va estudiar directament a Arquimedes, però és clar que ho va conèixer indirectament a través d'Eutocio i Giorgio Valle.

És estrany que no hagi sopat de Leonardo Algebra. Era difícil o massa abstracte?. Era, no obstant això, una geometria pura que substituïa el desconeixement teòric de l'espai pel seu poder visual. Les reflexions sobre els conceptes bàsics de la geometria són molt interessants, encara que la influència d'Aristòtil i Nicolás de Cusa és evident.

Leonardo no retrocedeix davant l'ús de conceptes infinitesimals (és el pas al límit). Per exemple, proposa dividir el centre de gravetat del semicercle en piràmides (triangles) de determinació, tantes piràmides com siguin necessàries perquè la fragilitat de les seves bases sigui inapreciable i gairebé directa. No obstant això, aquest és un cas excepcional i, en general, els mètodes de Leonardo són més simples, correctes i elementals.

Les idees intuïtives, probablement, li van portar al seu major descobriment, a calcular el centre de gravetat de la piràmide. Sembla que traslladant a l'espai el mateix raonament que va fer sobre el centre de gravetat del triangle del pla, passant pel tetraedre regular, va poder situar el seu centre de gravetat en el punt de tall dels seus eixos (és a dir, les rectes que uneixen un vèrtex amb el centre de gravetat del costat oposat) i al quart de la distància de la base.

Més tard va descobrir que les rectes que uneixen els punts centrals de les cantonades contra un tetraedre es tallen en el centre de gravetat. Finalment, va generalitzar el descobriment, indicant que el centre de gravetat de qualsevol piràmide es troba en el seu eix (de la base a la quarta part).

Les recerques sobre la transformació recíproca de sòlids es basen en “De transmutationibus geometricis” de Nicolás Cusa, qui aplica els mètodes de Vall per a resoldre problemes enunciats pel cusés (formant la confluència de diverses galledes, convertint una galleda en un prisma i viceversa). No obstant això, Leonardo també considera transformacions especials. Per exemple, entre el cub i la piràmide.

Leonardo també es va ocupar de les lumulas d'Hipócrates. A més dels nombrosos esments del seu Quaderns, en 1514 va intentar escriure un tractat: De ludo geomètric, que va quedar incomplet com tota la seva obra. S'entén que existeixi una certa passió pel valor estètic de les lumulas. De pas, a Occident va descobrir unes proposicions geomètriques que encara no es coneixien. Per exemple, va establir que la suma de les superfícies de les lumulas construïdes sobre els costats dels triangles equilàters era igual a la del triangle.

Cal esmentar l'enginyosa solució mecànica que Leonardo va trobar per al problema d'Òptica d'Al-Hazi amb un compàs especial. Aquesta solució de Leonardo indica profunds coneixements sobre les propietats dels talls cònics. Geomètricament 150 anys després va ser resolt per Huygens.

Les recerques sobre perspectiva realitzades per Leonardo es van publicar en el “Tractat de la pintura” en 1651.

Cal dir que a Leonardo se li deuen imatges i projectes d'eines matemàtiques, compassos de proporció i un parabológrafo que va utilitzar per a construir miralls parabòlics.

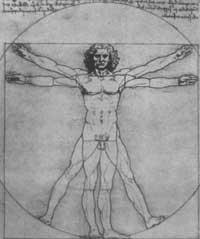
La influència de les matemàtiques també es pot apreciar en les seves pintures. Leonardo va codificar les proporcions del cos fent la geometria infraestructura de les seves pintures. La seva composició respon a un esquema harmònic fàcilment localitzable, amb estructures radials, troncs de con, triangles, arcs, espirals, trapezis, pentàgons, etc.