Leonardo-ren Matematika

Leonardo da Vinci (1452-1519) dugu Errenazimentuko zientzilarien eredua. Zientzigizon hau, ezaguna denez, zientziaren arlo askotan aritua zen: Anatomia, Optika, Botanika, Biologia, Geografia, Geologia, Mekanika, Geometria, Pintura, Eskultura, Hirigintza, Arkitektura, Astronomia, Nautika, Fisika, eta abarretan. Ez zegoen bere jakinminak ikertzera bultzatzen ez zuenik. Dena arakatu behar zuen.

Arteetan ezagunagoa bada ere, ezin ditugu beste arloetan egindako ekarpenak baztertu. Leonardo autodidakta izan zen eta, orduko beste zientzilariek ez bezala, ez zekien ez latina eta ez grekoa. Hala ere, horrek ez du esan nahi bere lanek oinarri sendorik ez zutenik. Aitzitik, lan batean (zientzian) murgiltzen zenean sakonki aztertzen zituen forma guztiak. Bere jakinmina hain handia zen, ezen egiten ari zen lana (artean) maiz uzten bait zuen.

Badakigu 1501ean Florentziara itzuli zenean, Luca Pacioli-rekin egon eta gero, Geometrian murgildu zela. Bitartean Santa Ana koadroaren zirrimarra bukatugabea besterik ez zuen egin. 1501. urteaz gero Geometriaz arduratu zen; 1504-1506 bitartean Hidraulikaz; 1505ean eskuskribu batean solidoen geometria aztertu zuen; 1510ean Anatomiak erakarri zuen; eta abar.

Konpas parabolikoa.

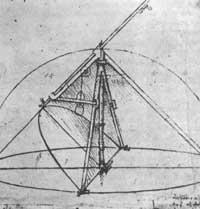
Baina, artikulu honetan hain ezaguna ez den Leonardoren matematika aipatu nahi dugu.

Leonardo gazteak Andrea Verrocchio-ren eskolan asko ikasi zuen. Verrocchioren lantegian pintura ezezik brontzea urtzen, harriak lantzen, planoak egiten, ubideak irekitzen, etxeak eraikitzen, eta abar ere ikasten zen. “Arte” guzti horietan iharduteko, pinturan ere perspektiba ezagutzeak garrantzi handia bait zuen, oinarri zientifiko (bereziki matematiko) izugarria eskatzen zen. Leonardoren formazioa praktikoa zen, funtsean Leonardo injinerua zen, makinagilea; ez teorikoa. Hori dela eta, bere geometria mekanikariarena da. Bilatzen dituen soluzioak praktikoak (tresna errealez egin daitezkeenak) dira eta ez teorikoak.

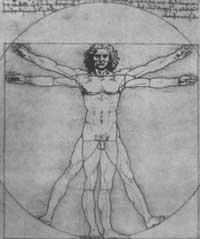
Joera praktiko horren adibide ditugu poligono erregularren eraikuntzari (zirkuluan inskribatutakoei) buruzko ikerlanak. Bere eskuskribuetan irudi horiek eta propietate asko azaltzen dira. Besteak beste, zirkuluaren koadraturari buruzkoak; 3, 6, 8, 24 aldeko poligonoen inskribatzea, (erraza da eta Leonardok konpasaren irekidura konstantez burutzen du) poligono erregularren eraikuntzarako hurbilketa (erregela eta konpasen bidez zuzenean eraiki ezin diren pentagono eta haptagonoa, esaterako, egitea zailagoa da, baina, Leonardok aski du soluzio hurbilduekin).

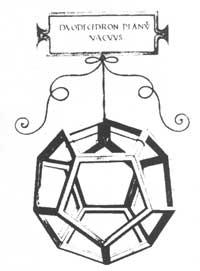
Seguraski bereak izango dira 1498an Luca Paciolik Ludovico Mairua-ri eskaini zion “Divina Proportione” kodea irudiz hornitzen duten poliedro erregular eta erdierregular beteak eta hutsak. Zirkuluaren zuzendapena eta koadratura, zirkulu edo arrabol bat zuzen baten edo plano baten gainean arrodatuz burutzen du. Soluzio horrek, problema teorikoa ez ezagutzea adierazten du. Hala ere, injineruaren ikuspegitik ulertzen da.

Pacioli. De Divina Proportione. 1509.

Ezpairik gabe, Leonardok Luca Pacioliri zor zion bere jakinduria matematikoa. Izan ere, Summa argitaratu bezain laster eskuratu zuen eta gero bere egilearekin adiskidetu egin zen. Bestalde, Alberto Saxoniakoa, Jordanus Nemorarius (askotan aipatzen zuena) eta Nikolas Cusakoa (dudarik gabe beregan eragina izan zuena) ere ezagutu zituen. Seguraski ez zuen Arkimedes zuzenean ikasi, baina, argi dago zeharka, Eutocio eta Giorgio Valla-ren bitartez, ezagutu zuela.

Arraroa da Leonardo Algebraz afanatu ez izatea. Zail edo abstraktuegia ote zen?. Geometra hutsa zen ordea, eta espazioari buruzko ezagutza teoriko eza bere begi-ahalmenaz ordezkatzen zuen. Geometriako oinarrizko kontzeptuei buruzko hausnarketak interesgarriak dira oso, Aristotele eta Nikolas Cusakoaren eragina nabaria bada ere.

Leonardok ez du kontzeptu infinitesimalen (limiterako urratsa da) erabilpenaren aurrean atzera jotzen. Esate baterako, zirkuluerdiaren grabitate-zentrua determinatzeko piramidetan (triangelutan) banatzea proposatzen du; beren oinarrien ahurtasuna ohartezina eta ia-ia zuzenak izan daitezen adina piramidetan banatzea hain zuzen. Hala ere, hori aparteko kasua da eta, oro har, Leonardoren metodoak sinple, zuzen eta elementalagoak dira.

Leonardo da Vinciren poliedro hutsak.

Ideia intuikorrek, seguraski, eraman zuten bere aurkikuntzarik handienera; piramidearen grabitate-zentrua kalkulatzera, alegia. Badirudi planoko triangeluaren grabitate-zentruari buruz egin zuen arrazonamendu bera espaziora trasladatuz, tetraedro erregularretik pasatuz, honen grabitate-zentrua kokatu ahal izan zuela, bere ardatzen (hau da, erpin bat kontrako aldearen grabitate-zentruarekin lotzen duten zuzenen) ebaki-puntuan eta oinarritik distantziaren laurdenera.

Leonardoren pinturetan soma daiteke matematikaren eragina. Leonardok gorputzaren proportzioak kodetu egin zituen, geometria bere pinturen azpiegitura eginez. Konposizioa erraz aurki daitekeen eskema harmoniko baten arabera dago egina; egitura erradial, kono enbor, triangelu, arku, kiribil, trapezio, pentagono eta abarren arabera.

Gero aurkitu zuen tetraedro baten aurkako ertzetako erdiko puntuak lotzen dituzten zuzenek grabitate-zentruan ebakitzen dutela elkar. Azkenik, aurkikuntza orokortu egin zuen, edozein piramideren grabitate-zentrua bere ardatzean (oinarritik horren laurdenera) dagoela esanez.

Solidoen elkarrekiko transformazioari buruzko ikerketak, Nikolas Cusakoaren “De transmutationibus geometricis” lanean daude oinarriturik, cusarrak enuntziatutako problemak ebazteko Vallaren metodoak aplikatzen dituelarik (zenbait kuboren bildura osatuz, kubo bat prisma bihurtuz eta alderantziz). Hala ere, Leonardok transformazio bereziak ere kontsideratzen ditu. Esaterako, kubo eta piramidearen artekoa.

Hipokratesen lunulez ere arduratu zen Leonardo. Bere Cuadernos-eko aipamen ugariez gain, 1514ean saiatu zen tratatu bat idazten: De ludo geometrico, bere obra osoa bezala osatu gabe geratu zena. Lunulen balio estetikoaz horrelako grina izatea ulertzen da. Bide batez, mendebaldean artean ezagutzen ez ziren proposizio geometriko batzuk aurkitu zituen. Adibidez, triangelu aldekideen aldeen gainean eraikitako lunulen azaleren batura triangeluarenaren berdina zela ezarri zuen.

Aipa dezagun Al-Hazin-en Optikako problemarako Leonardok konpas berezi baten bidez aurkitu zuen soluzio mekaniko burutsua. Leonardoren soluzio horrek ebakidura konikoen propietateei buruzko ezagumendu sakonak zituela adierazten du. Geometrikoki 150 urte geroago Huygens-ek ebatzi zuen.

Perspektibari buruz Leonardok egin zituen ikerketak “Pinturaren tratatua” lanean argitaratu ziren 1651n.

Leonardori besteak beste tresna matematikoen irudi eta proiektuak, proportzio-konpasak eta ispilu parabolikoak eraikitzeko erabili zuen parabolografo bat zor zaizkiola esan behar da.

Bere pinturetan ere soma daiteke matematikaren eragina. Leonardok gorputzaren proportzioak kodetu egin zituen, geometria bere pinturen azpiegitura eginez. Konposizioa erraz aurki daitekeen eskema harmoniko baten arabera dago egina; egitura erradial, kono-enbor, triangelu, arku, kiribil, trapezio, pentagono eta abarren arabera.