¿Imaginería?

1988/12/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

En este mundo en el que todos los seres, tanto los vivos como los inanimados, tenemos tres dimensiones: altura, anchura y grosor, aunque alguna de ellas pueda ser nula. A la hora de plasmar en una hoja bidimensional como la que vemos, utilizamos diferentes técnicas para introducir estas tres dimensiones en dos dimensiones.

Por ejemplo, si lo que queremos representar es un cuerpo geométrico, utilizaremos la técnica de la perspectiva. Si por el contrario el cuerpo es la cara de una persona, por ejemplo, la técnica de las sombras. Por supuesto, ambas se pueden utilizar simultáneamente.

En cuanto a la perspectiva, podemos decir que además de ser una rama de la Geometría, es una herramienta muy útil para los artistas. Y es que tanto los científicos como los artistas han visitado el XV. Se acepta lo que introdujeron en el siglo XIX, y científicos y artistas escribieron numerosos libros sobre perspectiva. Entre los artistas que utilizaron la técnica de la perspectiva destacan Filippo Brunelleschi, Piero della Francesca (autor del libro De perspectiva pingendi, entre otros), Leon Battista Alberti (autor del libro De pictura en este libro, que escribió un resumen de todos los descubrimientos de entonces sobre la Geometría aplicada a la imagen y la pintura), escribimos en el Tratado de la pintura horizontal (Adenda de la pintura).

Científicos: El traductor Federico Commandino (en 1558 publicó una obra sobre la perspectiva), Daniele Barbarbaro (autor del libro La práctica de la perspectiva ... obra muy útil a pintores, escultores y arquitectos), el arquitecto Jacopo Barozzi (autor del libro Las dos reglas de la perspectiva práctica), autor del libro Carribiolo, publicado en 1583. En él aparece por primera vez el siguiente teorema: se trata de un conjunto de perspectivas rectas y convergentes de un haz de rectas paralelas. En este libro el área de perspectiva alcanzó el nivel científico).

Es comprensible este espacio, los pintores de entonces (XIV. y XV. si pensamos que trataban de estudiar las bases científicas de su arte (siglos XVI). Uno de los mayores problemas que presentaban los artistas era la representación de rectas paralelas, que se resolvieron con perspectiva.

Pero dejando la historia volvemos a nuestro tema. Ahora sí, podemos decir que todo lo tridimensional se puede representar en una página. Si resolvemos este problema, demos la vuelta y veamos qué podemos responder a la siguiente pregunta: ¿Todas las imágenes bidimensionales representan un ser tridimensional?

Para presentar esta respuesta solo tienes que mirar las tres primeras imágenes.

En la primera imagen se tapa con un papel, primero la parte inferior (por debajo del centro) y luego la parte superior. Si lo haces, descubrirás cómo combinando imágenes de dos cosas tridimensionales se puede conseguir una imagen imposible, que no se puede materializar en tres dimensiones. El autor de esta imagen es Roger Hayward y su título es un monumento indecible. No podemos decir que la perspectiva juegue un papel importante en este efecto. Sin embargo, en la parte superior se utiliza la perspectiva y en la parte inferior la sombra para representar las tres dimensiones.

En la segunda y tercera figura, la perspectiva juega un papel importante, pero no como se podía esperar, es decir, para representar cosas que realmente existen, sino para expresar seres imposibles. ¡Sorprendente! Lo que fue la invención de Cristo, ahora se convierte en un rival y parece que sólo nos va a producir quebraderos de cabeza. Sin embargo, no debemos pensar así. Las imágenes no pierden su adorno. Por el contrario, ganan belleza, encanto, fascinación y misticismo.

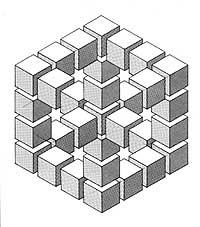
La segunda, aunque imposible, es distinta. En esta imagen se obtiene la representación óptica mediante la perspectiva. A primera vista parece que la imagen es real, es decir, que se puede materializar en tres dimensiones. Son sólo cubos. Pero si miras bien y siguiendo las líneas de cubo por diferentes caminos, te darás cuenta de que un cubo de un vértice tiene que estar a la vez a la altura y debajo del cubo del otro vértice. Esto nos dice que es imposible.

Este tipo de figuras imposibles las convirtió en arte. C. Escher. Puedes volver a ver otro cuadro aquí. Ya aparecían en los números 3 y 5. En esta tercera imagen tienes un trabajo titulado La relatividad. Escher nació en la localidad holandesa de Leeawarden en 1898 y ha estudiado en la Escuela de Arquitectura y Diseño Decorativo de Harlem. Su tipo de arte ha sido denominado arte matemático. Y es que, como ha dicho el propio Escher: "muchas veces me encuentro más cerca de los matemáticos que de los artistas". Su frase es: "todos mis trabajos son juegos. Juegos serios". Y eso es precisamente lo que se ve en la tercera figura, el juego de escaleras.

Otro tipo de imágenes son aquellas que ocultan dos imágenes. Te traemos:

En el cuarto tenemos un prisma cuadrado y un escarabajo (idea de introducir el escarabajo L.S. Penrose y R. Penrose fue padre e hijo). ¿Dónde ves el escarabajo dentro o fuera del prisma? Para conseguir ambos efectos debes mirar al prisma (no al escarzano) y acercar un vértice interno (es decir, suponer que está más cerca) o alejarlo (es decir, suponer que está más lejos) como quieras. Este efecto es también la influencia de la perspectiva.

La quinta imagen corresponde a la bandera canadiense, con la hoja de arce en la parte blanca central. Pero si lo miras con mucho cuidado también puedes ver a dos personas hablando. Inténtalo.

En el sexto, la joven anciana de Boring, conocida por su edad. En esta imagen mucha gente ve a un joven fascinante y otros muchos a una locura fea. ¿Qué ves tú? La respuesta permite dar interpretaciones diferentes sobre tu identidad. Pero eso es obra de otros y no de nosotros.

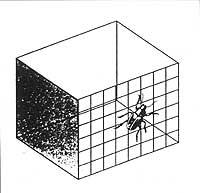
Otra representación para terminar. Al final de esta página tienes un clavo en la figura 7. Dejar la revista sobre la mesa, a la altura de un borde. Si miras de arriba a abajo los clavos, los verás tumbados en la página. Ahora flexiona ligeramente y coloca un ojo (cerrar el otro) en el punto que apuntan los clavos aproximadamente y mira los clavos a ras. En esta posición te parecerá que los clavos están clavados en la hoja. ¿No es así?