Infinito

1998/10/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

El infinito es difícil de definir y todas las definiciones tendrán argumentos a favor y en contra. Si nos dirigimos a un vocabulario común se define como aquel que no tiene fin y no puede ser indefinido. La definición es detallada y parece razonable. La intuición también va por ahí, pero ahora nos preguntamos ¿hay algo que no tiene límites? Si no hubiera nada sin límites, no definiríamos nada. Por lo tanto, hay que buscar algo sin límites.

La primera idea que viene a la mente es el universo, porque es lo más grande que conocemos. Sin embargo, hace 2.000 años Arquímedes demostró que el universo era también finito cuando calculó el número de granos de arena necesarios para llenar el universo, menos de 1063. A pesar de su gran cantidad, es finita. Muchas veces los seres humanos mezclamos infinito y cosas grandes. Muchas cosas son grandes pero tienen límites. Por lo tanto, no son infinitos.

Esto agota todas las posibilidades existentes en el mundo real/físico. Por tanto, tenemos que ir al mundo de la imaginación. En el mundo de la imaginación encontramos los mayores obstáculos para comprender el infinito, ya que el mundo de la imaginación es amplio y sin límites. Por otro lado, cada uno tiene su propia imaginación y para entendernos con otro amigo, el mundo de las ilusiones que yo tenía tiene que unir.

El propio Arquímedes nos dio la idea de encontrar algo sin límites. Él calculó la cantidad de granos de arena necesarios para llenar el universo. Este número de granos, 1063, era un número natural finito. Pero ¿los números que utilizamos para contar son finitos? No, claro. Ahí está algo ilimitado, el conjunto de los números naturales,

N = {1, 2, 3, 4, 5, ..., 1.000.000, 1.000.001, ..., 1063, ...}.

Si añadimos a los números naturales los opuestos, los negativos y los 0 obtendremos números enteros, que también son infinitos:

Z ={...., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...}.

El conjunto de números enteros es la parte del conjunto de números racionales. Por tanto, los números racionales también son infinitos:

Q = anteriores..., -3, -1/3, -1/2, -2, -1, 0, 1, 2, 1/2, 1/3, 3, ...}.

Finalmente, añadiendo irracionales a los números racionales (…e,p,…) obtendremos números reales que también son infinitos. Por lo tanto, hemos elaborado una cadena como la siguiente:

N C Z C Q C R.

En él todos los conjuntos son infinitos.Cuando
contamos los elementos de los conjuntos finitos se define la aplicación bijetiva entre el conjunto y un subconjunto del grupo N. Por ejemplo, conjunto de vocales = {a, e, i, o, u}. ¿Cuántos elementos tiene?

a -1, e -2, i -3, o -4, u -5

Por lo tanto, entre los grupos {a, e, i, o, u} y {1, 2, 3, 4, 5} hemos definido una aplicación bijetiva.Los grupos finitos
tienen distintos elementos: el conjunto de vocales 5 elementos, el conjunto de consonantes 21 elementos. ¿Qué pasará con los conjuntos infinitos?

Para saber cuántos elementos hay en el grupo Z más que en el grupo N utilizaremos el hotel infinito, el hotel N. Supongamos un hotel con infinito habitaciones (1º, 2º, 3º, …) todas las habitaciones están llenas. Debido a una mala comunicación, un grupo de infinitos amigos se adelanta un día y los responsables del hotel deben proporcionarles una habitación para corregirla. ¿Cómo introducirán los nuevos infinitos amigos (-1, -2, -3, ...) en cada habitación los responsables del hotel?

Una solución puede ser: (-1) meter al nuevo amigo en la habitación 1, meter al compañero de la habitación 1 (1) en la habitación 2, meter al compañero de la habitación 2 (2) en la habitación 3 y así con los demás. Al primer amigo le hemos adaptado su habitación. Ahora situaremos (-2) al segundo amigo. Introducimos al compañero (-2) en la habitación 1, pasamos al compañero (-1) en la habitación 1 a la habitación 2. Amigo de 2º (1) habitación a 3º y así con los demás. En general, para introducir un nuevo amigo, empezando por la primera habitación, las personas que se encuentren en las habitaciones pasarán a las siguientes habitaciones y dejaremos el primero vacío.

En el último momento (0) han llegado nuevos amigos a buscar sitio. Siguiendo el procedimiento anterior, vaciaremos la 1ª habitación para acceder a ella.

Así pues, en el Hotel N había amigos 1, 2, 3, ... y hemos incluido -1, -2, -3, ... y 0 personas, adaptando cada uno de ellos en una habitación. En consecuencia, podemos decir que hay tantas personas como habitaciones. Es decir, tienen tantos elementos como los grupos Z y N.

Habitaciones	1.	2.	3.	4º	5.	...
Hotel completo	1.	Servicios	Servicios	Seguridad	Servicios	...
Introducir un nuevo amigo	-1	1.	Servicios	Servicios	Seguridad	...
Añadir nuevo amigo 2	-2	-1	1.	Servicios	Servicios	...

Otro día hemos vuelto a encontrar el hotel N lleno. Pero a mediodía infinitas personas han dejado el hotel. Estimados amigos, 4º, 6º, … estaban en las habitaciones. Por lo tanto, la mitad de las habitaciones han quedado vacías. Por la tarde ha venido otro grupo infinito (1,2,3, ...). Los responsables del hotel no han tenido problemas para adaptarse a las habitaciones vacías. (1) meter al compañero en la habitación 2, (2) al compañero en la habitación 4, (3) al amigo en la habitación 6 y así con los demás.

Habitaciones	1.	2.	3.	4º	5.	6º	...
Hotel completo	a)	b)	c)	d)	e	f)	...
Medio hotel vacío	a)		c)		e		...
Hotel de nuevo lleno	a)	1.	c)	Servicios	e	Servicios	...

Podemos decir que en el centro de las habitaciones hemos metido tantas personas como en todo el hotel. En otras palabras, un conjunto infinito (1,2,3,...) puede tener tantos elementos como subconjuntos infinitos (2,4,6,...).

El siguiente grupo es Q, los números racionales son cocientes entre dos números enteros, sin que el divisor sea 0. Los cocientes para contar los números del grupo Q serán considerados como un número único. Como en el caso anterior, demostraremos que en el grupo Q hay tantos números como en el grupo N mediante una aplicación bijetiva. Esta aplicación la proporcionaremos mediante una tabla en la que sólo aparecerán los números positivos, pero los números negativos se contabilizarán de la misma manera.

Los números que indican las fracciones entre paréntesis ya han aparecido. Por eso no se computan en la tabla inferior.

1349101827…281626…5715192939…6142538…11132024374353…123652…21233035445168…22345067…..........................

A partir de esta tabla se puede comprobar que por cada elemento del grupo N hay un elemento del grupo Q y por el contrario, por cada elemento del grupo Q hay un elemento del grupo N. En definitiva, se puede demostrar que la aplicación es un bijetivo.

Todos estos infinitos conjuntos parecen tener el mismo número de elementos, A1. En el grupo siguiente, R, además de los números racionales, se incluyen los números irracionales. ¿Cuántos son los números irracionales? Antes de contar todos los números reales contabilizaremos los comprendidos entre 0 y 1.

Comprobamos que en el intervalo (0,1) hay más números que en el grupo N. La idea de la demostración es: Suponemos que entre los grupos N y (0,1) la aplicación bijetiva está definida y veremos que un número situado entre 0 y 1 no tiene imagen en el grupo N. Por lo tanto, concluiremos que no es posible definir este tipo de aplicaciones. de donde se deduce que en el grupo (0,1) hay más elementos que en el grupo N. Este mayor número de elementos se denominará c y se cumplirá con A1 < c. Vamos a explicar la demostración.

Si entre los grupos N y (0,1) estuviera definida la aplicación bijetiva, podríamos escribir la siguiente correspondencia:

Números naturales (0,1)
alternos intercalos10,a1a2a3a4a5 ...20,b1b2b3b3b4b5 ...30,c1c2c3c4c5 ....40,d1d3d4d5 ....50,e1e2e3e4e5 ..........

A la izquierda todos los números naturales y a la derecha, en forma decimal, todos los elementos del grupo (0,1). Tomemos los siguientes números:

z1a1, z2b2, z3c3, z4d4, z5e5,...

y completemos el siguiente número decimal:

0,z1z2z3z4z5...

Este número está entre 0 y 1 y no es el mismo que los que aparecen a la derecha porque así hemos elegido (z1a1, z2b2, z3c3, z4d4, z5e5, ...). Por lo tanto, no corresponde ningún elemento del grupo N situado a la izquierda. En el grupo (0,1) hay más elementos que en el grupo N.

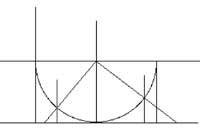
El rango (0,1) es sólo una pequeña parte del conjunto R, pero tiene más elementos que el conjunto N. Comparemos ahora los grupos (0,1) y R. La comparación la realizaremos mediante una figura geométrica.

En el eje OX de las coordenadas del plano se sitúa el intervalo (0,1). (1/2,1/2) se dibuja una semicircunferencia superior con centro y radio 1/2. Desde el punto x del intervalo (0,1) se eleva una vertical hasta alcanzar la media circunferencia. Se dibuja la recta que pasa por el centro de la circunferencia y por el punto anterior. Esta recta cortará el eje OX en el punto y. y es el punto correspondiente a x. También se puede hacer al revés. Tomando el punto y´ del grupo R, se dibuja la recta que une este punto con el centro de la circunferencia. Esta recta corta la semicircunferencia en un punto. Desde este punto baja unida al eje OX hasta encontrar el eje OX en el punto x´. x´ corresponde al punto y´.

Así, entre los grupos (0,1) y R se ha definido una aplicación bijetiva. Esto significa que los grupos (0,1) y R tienen el mismo número de elementos, es decir, c.

Igual que el número 1 es el siguiente 2 del número natural, podemos llamar A2 al siguiente del infinito A1 y A3 al siguiente y así sucesivamente. También hemos encontrado el infinito c y hemos demostrado que A1 < c. La pregunta que nos viene ahora a la mente es: ¿existe el infinito c A2? Es decir, ¿existe c = A2? Esta pregunta está por el momento pendiente de respuesta.

La aritmética de los números finitos es conocida, mientras que la de los números infinitos no. Se podría demostrar que:

A1 + n = A1c + n = cA1 + A1 = A1c + A1 = cn . A1 = A1c + c = cA1 . A1 = A1n . c = c(A1)n = A1c . c = c(2)A1 = (A1)A1 ⁼ c(c)n = c(c)A1 = c(2)c ⁼ (c)c = (c)c = otro ^infinito

A1 N es el número de elementos de los conjuntos Z y Q. c es el
número de elementos del conjunto R. En todos ellos n
es el número normal.

El resultado final significa que hay diferentes números infinitos.