Infinitua

Infinitua definitzea zaila da eta definizio guztiek izango dituzte aldeko eta kontrako argudioak. Hiztegi arrunt batera jotzen badugu, honela definitzen da: amaierarik ez duena eta izan ezin duena, mugagabea. Definizioa xehea da eta zentzuzkoa dirudi. Intuizioak ere hortik jotzen du, baina, orain, gure galdera hau da: ba al dago mugarik ez duen ezer? Mugarik gabeko ezer ez balego, ez genuke ezer definituko. Beraz, mugarik ez duen zerbait bilatu behar da.

Burura datorkigun lehenengo ideia unibertsoa da, izan ere ezagutzen dugun gauzarik handiena baita. Baina, duela 2.000 urte Arkimedes-ek unibertsoa ere finitua zela frogatu zuen, unibertsoa betetzeko behar ziren harea-pikorren kopurua kalkulatu zuenean; 1063 baino gutxiago, hain zuzen. Kopuru hori handia izan arren, finitua da. Askotan, gizakiok infinitua eta gauza handiak nahastu egiten ditugu. Gauza askok handia izan arren muga dute. Beraz ez dira infinituak.

Horrek mundu errealean/fisikoan egon litezkeen aukera guztiak agortzen ditu. Hortaz, irudimenaren mundura jo beharko dugu. Irudimenaren munduan, hain zuzen, aurkituko ditugu oztoporik handienak infinitua ulertzeko, irudimenaren mundua zabala eta mugarik gabekoa baita. Bestalde, norberak bere irudimena du eta beste lagun batekin elkar ulertzeko bion irudimenen munduek bat egin behar dute.

Arkimedesek berak eman zigun ideia mugarik gabeko zerbait aurkitzeko. Berak unibertsoa betetzeko zenbat harea-pikor behar zen kalkulatu zuen. Pikorren kopuru hori, 1063, zenbaki arrunt finitua zen. Baina zenbatzeko erabiltzen ditugun zenbakiak finituak al dira? Ez, jakina. Horra hor mugagabea den zerbait, zenbaki arrunten multzoa,

N = {1, 2, 3, 4, 5, ...., 1.000.000, 1.000.001, ...., 1063, ....}.

Zenbaki arruntei aurkakoak, negatiboak, eta 0 eransten badizkiegu zenbaki osoak lortuko ditugu, eta horiek ere infinituak dira:

Z = {...., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ....}.

Zenbaki osoen multzoa zenbaki arrazionalen multzoaren partea da. Hortaz, zenbaki arrazionalak ere infinituak dira:

Q = {...., -3, -1/3, -1/2, -2, -1, 0, 1, 2, 1/2, 1/3, 3, ....}.

Azkenik, zenbaki arrazionalei irrazionalak (¯_2 ,e,p, ....) erantsiz gero zenbaki errealak lortuko ditugu, eta horiek ere infinituak dira. Beraz, honelako katea osatu dugu:

N C Z C Q C R.

Bertan multzo guztiak dira infinituak.
Multzo finituen elementuak zenbatzen ditugunean multzoa eta N multzoaren azpimultzo baten artean aplikazio bijektiboa definitzen da. Adibidez, bokalen multzoa = {a, e, i, o, u}. Zenbat elementu dauka?

a -1, e -2, i -3, o -4, u -5

Beraz, {a, e, i, o, u} eta {1, 2, 3, 4, 5} multzoen artean aplikazio bijektiboa definitu dugu.
Multzo finituek elementu-kopuru desberdinak dituzte: bokalen multzoak 5 elementu, kontsonanteen multzoak 21 elementu. Multzo infinituekin zer gertatuko da?

Z multzoan N multzoan baino zenbat elementu gehiago dagoen jakiteko, hotel infinitua, N hotela, erabiliko dugu. Suposa dezagun infinitu logela duen hotel batean (1., 2., 3., ....) logela guztiak beterik daudela. Komunikazio oker bat dela eta, infinitu lagun duen talde bat egun bat aurreratu da eta hoteleko arduradunek logela bana eman behar diete, okerra zuzentzeko. Nola sartuko dituzte infinitu lagun berriak (-1, -2, -3, ....) logela banatan hoteleko arduradunek?

Hau izan daiteke soluzio bat: (-1) lagun berria 1. logelan sartu, 1. logelako (1) laguna 2. logelan sartu, 2. logelako (2) laguna 3. logelan sartu, eta horrela besteekin. Lehenengo lagun berriari bere logela egokitu diogu. Orain, (-2) bigarren lagun berria kokatuko dugu. (-2) laguna 1. logelan sartuko dugu, 1. logelan dagoen (-1) laguna 2. logelara pasatuko dugu. 2. logelako (1) laguna 3. logelara, eta horrela besteekin. Oro har, lagun berri bat sartzeko, lehenengo logelatik hasita, logeletan dauden lagunak hurrengo logeletara pasatuko dira eta lehenengoa hutsik utziko dugu.

Azken unean, (0) lagun berri heldu da leku bila. Aurreko prozedura erabiliz 1. logela hustuko dugu bera sartzeko.

Hortaz, N hotelean 1, 2, 3, .... lagunak zeuden eta -1, -2, -3, .... eta 0 lagun berriak sartu ditugu, bakoitza logela batean egokituz. Ondorioz, logela adina lagun dagoela esan dezakegu. Hots, Z eta N multzoek adina elementu dute.

Logelak	1.	2.	3.	4.	5.	....
Hotela beterik	1	2	3	4	5	....
Lagun berri bat sartu	-1	1	2	3	4	....
2. lagun berria sartu	-2	-1	1	2	3	....

Beste egun batean N hotela berriro aurkitu dugu beterik. Baina eguerdian infinitu lagunek utzi egin dute hotela. Lagun horiek 2., 4., 6., .... logeletan zeuden. Beraz, logelen erdia hutsik geratu da. Arratsaldean beste talde infinitua etorri da (1,2,3, ....). Hoteleko arduradunek ez dute arazorik izan logela hutsetan egokitzeko. (1) laguna 2. logelan sartu, (2) laguna 4. logelan, (3) laguna 6. logelan eta horrela besteekin.

Logelak	1.	2.	3.	4.	5.	6.	....
Hotela beterik	a	b	c	d	e	f	....
Hotel erdia hutsik	a		c		e		....
Hotela berriro beterik	a	1	c	2	e	3	....

Logelen erdian hotel osoan adina lagun sartu dugula esan dezakegu. Bestela esan, multzo infinitu batek (1,2,3,...) bere azpimultzo infinitu (2,4,6,...) adina elementu izan dezake.

Hurrengo multzoa Q da, zenbaki arrazionalak bi zenbaki osoren arteko zatidurak dira, zatitzailea 0 izan gabe. Q multzoko zenbakiak zenbatzeko zatidurak zenbaki bakartzat hartuko ditugu. Aurreko kasuan bezala Q multzoan N multzoan adina zenbaki dagoela frogatuko dugu aplikazio bijektibo baten bidez. Aplikazio hori taula baten bidez emango dugu, taulan zenbaki positiboak bakarrik agertuko dira, baina zenbaki negatiboak era berean zenbatu behar dira.

Parentesien arteko zatikiek adierazten dituzten zenbakiak jada agertu dira. Horregatik ez dira zenbatzen beheko taulan.

1349101827…281626…5715192939…6142538…11132024374353…123652…21233035445168…22345067…...........................

Taula horretan oinarrituta froga liteke N multzoaren elementu bakoitzeko Q multzoaren elementu bat dagoela, eta, alderantziz, Q multzoaren elementu bakoitzeko N multzoaren elementu bat dagoela. Laburbilduz, aplikazioa bijektiboa dela froga liteke.

Badirudi multzo infinitu horiek guztiek elementu-kopuru bera, A1, dutela. Hurrengo multzoan, R, zenbaki arrazionalez gain zenbaki irrazionalak sartzen dira. Zenbat dira zenbaki irrazionalak? Zenbaki erreal guztiak zenbatu baino lehen 0 eta 1 artean daudenak zenbatuko ditugu.

(0,1) tartean N multzoan baino zenbaki gehiago dagoela frogatuko dugu. Frogapenaren ideia hau da: N eta (0,1) multzoen artean aplikazio bijektiboa definiturik dagoela suposatuko dugu eta 0 eta 1 artean dagoen zenbaki batek N multzoan irudirik ez duela ikusiko dugu. Beraz, horrelako aplikaziorik ezin dela definitu ondorioztatuko dugu. Eta hortik (0,1) multzoan N multzoan baino elementu gehiago dagoela aterako dugu. Elementu-kopuru handiago hori c izendatuko dugu eta A1 < c beteko da. Goazen frogapena azaltzera.

N eta (0,1) multzoen artean aplikazio bijektiboa definiturik balego, honelako korrespondentzia idatz genezake:

Zenbaki arruntak(0,1) tarteko
zenbaki errealak10,a1a2a3a4a5 ....20,b1b2b3b4b5 ....30,c1c2c3c4c5 ....40,d1d2d3d4d5 ....50,e1e2e3e4e5 .............

Ezkerraldean zenbaki arrunt guztiak eta eskuin aldean, era hamartarrean idatzita, (0,1) multzoko elementu guztiak. Har ditzagun zenbaki hauek:

z1a1, z2b2, z3c3, z4d4, z5e5, ....

eta osa dezagun zenbaki hamartar hau:

0,z1z2z3z4z5....

Zenbaki hori 0 eta 1 artean dago, eta ez da eskuinaldean agertzen direnen berdina horrela aukeratu dugulako (z1a1, z2b2, z3c3, z4d4, z5e5, ....). Beraz, ez dagokio ezkerrean dagoen N multzoko elementu bat ere. (0,1) multzoan, beraz, N multzoan baino elementu gehiago dago.

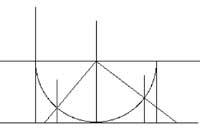
(0,1) tartea R multzoaren zati txikia besterik ez da, baina N multzoak baino elementu gehiago dauka. Konpara ditzagun, orain, (0,1) eta R multzoak. Konparaketa irudi geometriko baten bidez egingo dugu.

Planoko koordenatuen OX ardatzean (0,1) tartea kokatzen da. (1/2,1/2) zentroa eta 1/2 erradioa dituen goiko zirkunferentzierdia marrazten da. (0,1) tarteko x puntutik bertikal bat altxatzen da zirkunferentzierdia jo arte. Zirkunferentzierdiaren zentrotik eta aurreko puntutik pasatzen den zuzena marrazten da. Zuzen horrek OX ardatza y puntuan ebakiko du. y da x-ri dagokion puntua. Alderantziz ere egin daiteke. Har dezagun R multzoko y´ puntua, puntu hori eta zirkunferentzierdiaren zentroa lotzen dituen zuzena marrazten da. Zuzen horrek zirkunferentzierdia puntu batean ebakiko du. Puntu horretatik OX ardatzarekiko elkartzuta jaisten da OX ardatza x´ puntuan aurkitu arte. x´ da y´ puntuari dagokiona.

Horrela, (0,1) eta R multzoen artean aplikazio bijektiboa definitu da. Horrek (0,1) eta R multzoek elementu-kopuru bera dutela esan nahi du, c alegia.

1 zenbaki arruntaren hurrengoa 2 den bezala, A1 infinituaren hurrengoari A2 dei diezaiokegu, eta hurrengoari A3, eta horrela etengabe. Bestalde c infinitua ere aurkitu dugu eta A1 < c dela ere frogatu dugu. Orain burura datorkigun galdera hauxe da: ba al da c A2 infinitua? Hots, ba al da c = A2? Galdera hori erantzun gabe dago oraingoz.

Zenbaki finituen aritmetika ezaguna dugu, zenbaki infinituena, aldiz, ez. Berdintza hauek froga litezke:

A1 + n = A1c + n = cA1 + A1 = A1c + A1 = cn . A1 = A1c + c = cA1 . A1 = A1n . c = c(A1)n = A1c . c = c(2)A1 = (A1)^A1 = c(c)n = c(c)^A1 = c(2)^c = (c)^c = beste infinitu bat

A1 N, Z eta Q multzoen elementu-kopurua da.
c R multzoaren elementu-kopurua da.
Guztietan n zenbaki arrunta da.

Azken emaitzak zenbaki infinitu desberdinak daudela esan nahi du.