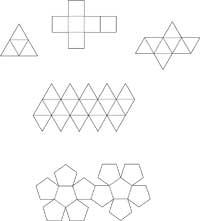
Platonic bodies

1998/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

No, those strong, slender and dark-haired bodies that we see in the sun or in the shade during the summer holidays. No, they are also not those who do bodybuilding. It is also wrong to think of the roasted lambs that are served in “Platós”. Platonic bodies are only regular polyhedra. Regular polyhedra have also been called cosmic body or platonic body by the forms that Plato applies in his work Timeo to scientifically explain phenomena. In total there are five: tetrahedron, hexahedron (cube), octahedron, dodecahedron and ikosaedro (figure 1). The five are characterized by being formed by regular polygons of the same type and convex; the tetrahedron, octahedron and icosahedron are formed by equilateral triangles, the square hexahedron and the pentagon dodecahedron.

Nombredelescanterpinactetraedro4 trianglo64Hexaedroa6 quadatu128Octaedro8 triangulo126 Dodecaedroa12 pentagono3020Ikosaedroaedro20 triangular 3012

Formula of Euler

Sides + Vertices = Edges + 2

Plato (BC) 427-347) did not in itself imply technical results for mathematics. However, it was the real center of the mathematical activity of the time and in addition to personally influencing its development, it also led it. The doors to the school of Athens read: “Not among anyone who does not know geometry.” His mathematical responsibility, rather than as mathematics, made him known as mathematics. It seems that Plato's recognition of mathematics did not come from his master Socrates. Architect, his friend, was the one who approached mathematics Plato. In the year 300 he visited him in Sicily. Perhaps there he first met the five regular bodies mentioned.

Tetrahedron, hexahedron, octahedron and ikosaedro were related to the four elements of Enpedokles in a cosmic scheme that has fascinated man for centuries (Figure 2). On the other hand, the Pythagoras admired the dodecahedron. Plato recognized the dodecahedron, fifth and last regular body, as a symbol of the universe.

Fire, air, water and soil are joined with tetrahedron, octahedron, ikosaedro and hexahedron respectively. Except those of the hexahedron, since the sides of the other polyhedra are equilateral triangles and, therefore, similar, the corresponding elements, fire, air and water, could become mutual, but not lands, since the faces of the hexahedron are square. Squares cannot be broken down into equilateral triangles, only they can be broken down into isosceles right triangles. On the other hand, the smaller polyhedron compared to its surface is the tetrahedron, from which the bond to fire appears to be detached. The most voluminous on the surface is the ikosaedro, so it has joined the water. The hexahedron, for its part, is stable with respect to its base, so it has joined the ground. By turning the octahedron grasped by two opposite vertices, it has adapted to the moving air. The fifth regular polyhedron, dodecahedron, consists of pentagons and the pentagons cannot be broken down into equilateral triangles, and the dodecahedron has 12 sides, reflecting the 12 signs of the zodiac, hence its relationship with the universe.

In Timeo, where he bears the name of his main interlocutor, he expounded his ideas on the regular platonic bodies. We do not know whether Timeo Lokia's actually existed or Plato invented it with the excuse of explaining his Pythagorean ideas.

Plato wrote this colloquium at the age of 70, in which he gives us the first accurate trace of the relationship between the four elements and the regular bodies, but many of the episodes of this fantasy are due to the Pythagoreans. According to Proklo, Pythagoras built the cosmic image, but scholastic Suidas said that Teetetus (friend of Plato, a. C.). Born in 414, he was the first to write about it.

Euklides dedicated the last book of “Elements”, 13th, to the regular polyhedra. In it he gave us relations between the edges of the polyhedra and the radii of the inscribed and circumscribed spheres. Finally, as a motto appeared the theorem that was added later: besides the five regular polyhedra known, there is no other regular polyhedron.

XIII Elements of Euklides. According to a school of unknown date of the book, the Pythagoreans only knew three regular bodies and the octahedron and the icosahedron were known by Teetetus. However, it seems that Teetetus performed one of the systematic analyses then of the regular polyhedra and he himself wrote the theorem that there are five and only five regular polyhedra. Apika, in the last book of “Elements”, is also his calculations of the causes between the edges of the regular bodies and the radius of the circumscribed sphere.

Both in arithmetic and geometry, Plato positioned himself in favor of pure mathematics, against the materialistic conceptions of the craftsman and technician. Plutarko collected in his work “The Life of Marcelo” Plato’s anger at the use of mechanical artifacts in geometry; Plato considered this use as corruption and the simple cancellation of the existing good in geometry, giving his back brazenly to objects without a body of pure intelligence. Consequently, Plato could be, to a large extent, responsible for the main constraint to geometry constructions that can only be made by compass and ruler. The reason for this reduction was probably not the simplicity of the instruments used, but the symmetry of the constructed ones: any diameter of the circle is the axis of symmetry; any point of the line is the center of symmetry; any union with a straight line is its axis of symmetry.

Platonic philosophy, divinizing ideas, had to put first the straight line and the circumference between all geometric figures. Similarly, Plato exalted the triangle. For Plato, the differences of the five regular polyhedra were not mere triangles, squares, and pentagons. For example, each side of the tetrahedron consisted of six minor straight triangles (obtained by heights), decomposing the tetrahedron into 24 straight escalene triangles. Likewise, octahedron and icosahedron in 48 and 120 scalene straight triangles, respectively, and hexahedron in 24 isosceles right triangles.

Plato gave a special role to the dodecahedron, as representative of the universe, saying that “God used it entirely” (Timaeus, 55). Plato considered the dodecahedron as a set of 360 straight triangles escalenos, since drawing in the pentagons the five diagonals and the intermediate are 30 triangles.

By uniting the first four regular polyhedra with the four elements of the universe, Timeon gave a beautiful unified theory of matter, according to which everything is formed by ideal rectilinear triangles and physiology, as a whole, like the science of inert matter, is based on the functioning of such triangles. The growth of an animal's body, for example, explained:

“The Constitution of the Creature, in its entirety, when it is still young and its components are of recent construction, its tips are strongly interrelated… Any of the triangles that make up food and drinks…, older and weaker than yours, they cut it their newly made triangles and therefore it takes the best advantage and that is what makes the animal grow quiet.In old age, on the contrary, the triangles that form the body breaks