Quand la fiction devient réalité

2014/05/01 Azkune Galparsoro, Gorka - Ikertzailea eta irakasleaEuskal Herriko Unibertsitateko Informatika Fakultatea Iturria: Elhuyar aldizkaria

• Fisika
• Sariak

Quantique, toujours quantique

L'idée scientifique qui se rapproche le plus du type de télétransport que nous avons vu dans des séries comme Start Trek est le télétransport quantique, dont l'objectif est de transporter un système quantique du point A au point B, sans aucun support ou canal physique. Mais pour comprendre tout cela correctement, nous devons expliquer quelques-unes des bases de la physique quantique. Ne paniquez pas ! Parce que nous le ferons d'une manière très simple.

Boîtes et billes

Quand on parle de systèmes quantiques, on parle de concepts comme les atomes, les électrons, les protons ou les photons. Pour faciliter les choses, les systèmes quantiques seront des billes spéciales gardées dans des boîtes spéciales. Ces billes peuvent avoir deux couleurs : rouge G polluo bleu U. La première particularité de ces billes, c'est que, tout en restant à l'intérieur de la boîte, ils peuvent être dans un état de combinaison d'G liveshow et U couleurs:

classé

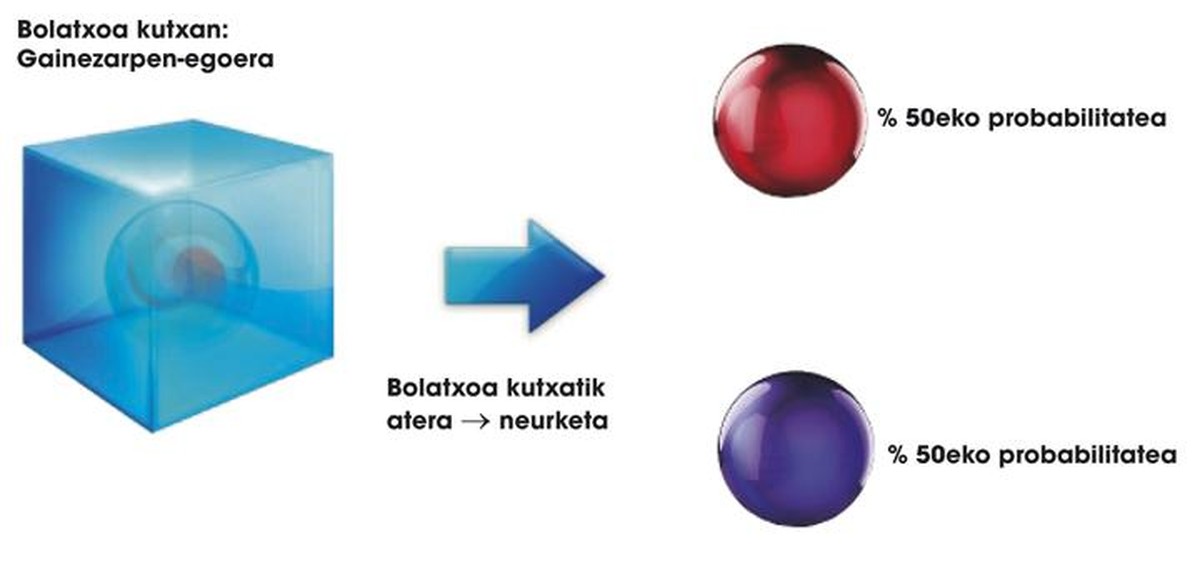
où a et b sont deux nombres réels. Sa signification est simple: ils indiquent la probabilité de la couleur que la bille aura en sortant de la boîte. En d'autres termes, si une bille est en état 0,5 G over + 0,5 U, alors que la probabilité d'avoir agi est ouverte de 50%. Dans la quantique cette propriété des billes est appelée propriété de la superposition. Cela nous amène à une autre loi spéciale: les billes à l'intérieur de la boîte peuvent être en état de chevauchement, mais lorsque nous ouvrons la boîte, elles ne peuvent être organisées qu'après. Il n'y a pas de superposition hors de la boîte. Le synonyme quantique d'ouverture de boîte est la mesure, où l'état de chevauchement des billes est annulé (voir figure 1).

Cependant, les boîtes ne sont pas utilisées uniquement pour stocker des billes. Si vous secouez la boîte différemment, nous pouvons changer l'état de la bille, par exemple en changeant les proportions des combinaisons. L'équivalent de l'agitation sont des opérations quantiques. Il y a beaucoup de types et nous n'allons pas approfondir. Pour le moment, il pense qu'en agitant la boîte, nous sommes capables de réaliser les opérations que nous voulons.

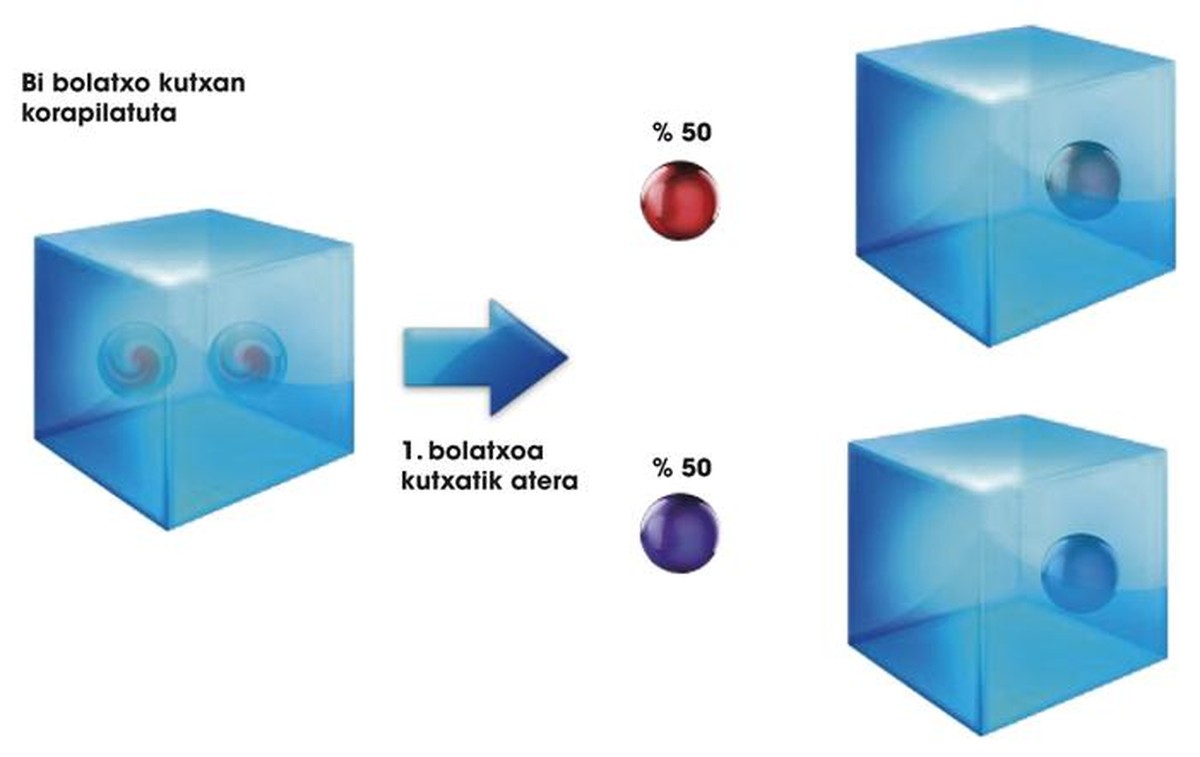
Pour terminer avec cette section, nous devons mentionner une autre particularité de nos boîtes et billes. Si nous plaçons deux billes dans la même boîte et agiter la boîte, nous pouvons couronner les billes ensemble. Ainsi, en agitant la Bolite 1 et la Bolite 2 dans la même caisse, nous pouvons obtenir l'état 0,5 G 1 G 2 + 0,5 U 1 U 2. En quantique, cette situation est appelée compliquée, car les deux billes sont compliquées. Dans cette situation, si l'on sort de la boîte seulement la bille 1 et que l'on voit qu'elle est en état G, on sait déjà que sans avoir à sortir de la boîte, la bille 2 sera en état d'état G (voir figure 2). Notez que ce n'est pas possible si les deux billes sont dans deux boîtes, même si elles sont superposées. En l'occurrence, si la première bille et G négocient, la deuxième bille peut être G négociée ou U. Il n'y a aucune relation entre les deux.

De nombreuses études sont menées sur les difficultés. Après avoir compliqué deux billes, elles restent compliquées jusqu'à ce qu'une mesure soit réalisée, même si la distance entre elles est très grande. Quelle que soit la distance, la mesure dans une bille agit brusquement sur l'autre bille et change son état même si nous ne l'avons pas touchée. Nous ne savons toujours pas pourquoi et comment il est compliqué, mais nous sommes déjà en mesure de l'utiliser. Comme vous pouvez l'imaginer, c'est la clé pour obtenir le télétransport.

Figure . Principe de superposition et mesure dans le cas d'une bille. Ed. Gorka Azkune

Figure . Le début de l'embrouillement et ses conséquences avec deux billes. Ed. Gorka Azkune

Rapport quantique

Nous avons deux bons amis, Alaitz et Beñat, et un jour ensemble ils ont décidé de compliquer deux boules. Après l'enchevêtrement, chacun a pris sa bille dans une boîte spéciale, sans jamais regarder la bille. Ainsi, quand chacun se déplaçait chez lui, les deux billes restaient emmêlées, bien qu'éloignées.

Alaitz a une autre bille chez elle, mise dans une autre boîte, dans un état de superposition inconnu. Alaitz, amoureux des défis, pense: « Comment envoyer à Beñat la nouvelle bille dans la situation où elle se trouve sans quitter la maison ? ". Il ne peut pas sortir le ballon de la boîte, car dans ce cas, il changerait son état naturel à G et autrement U. Il veut envoyer la bille à Beñat dans son état naturel, c'est à dire, à G + b onsU en situation de chevauchement. Alaitzena semble difficile, non ?

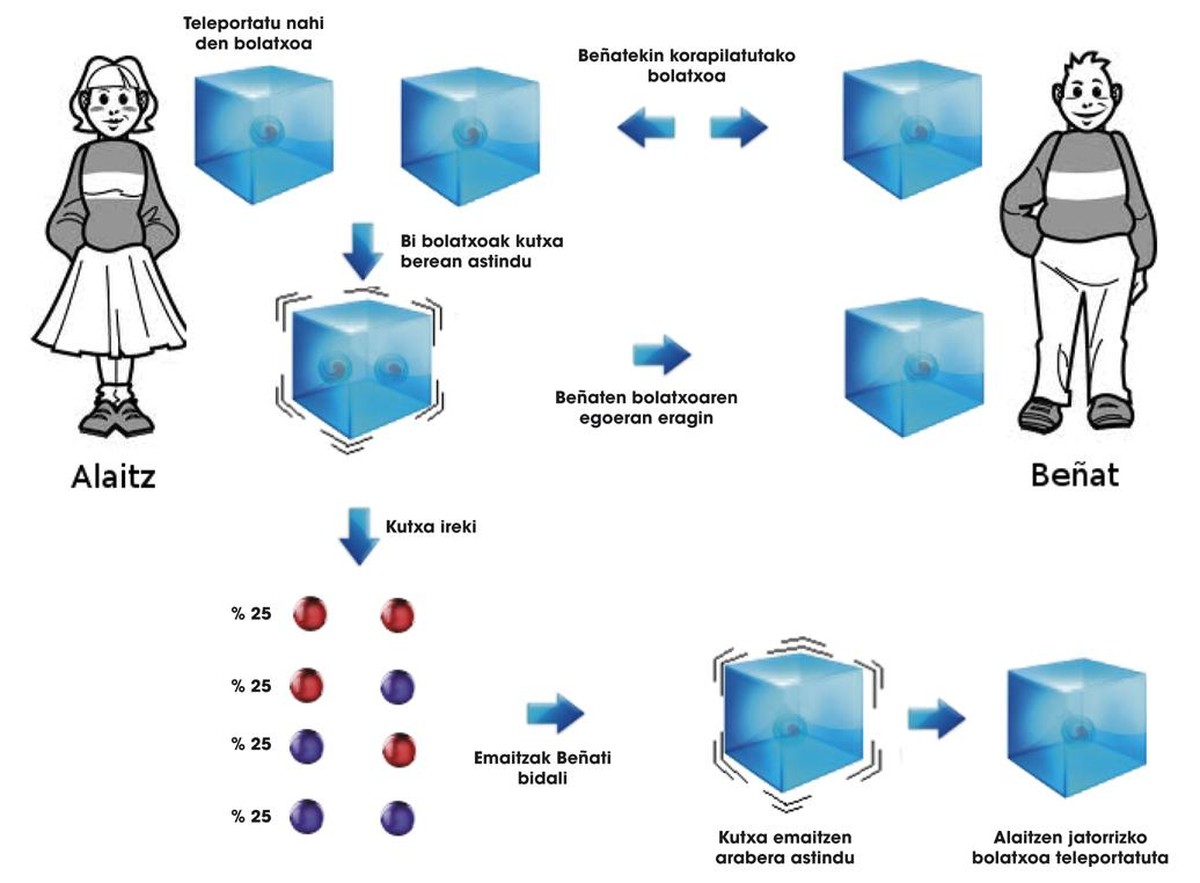
Mais comme Alaitz est une fille intelligente, elle trouve une solution. La bille qui veut envoyer Beñat la place dans la même boîte qu'elle avait déjà enveloppée de Beñat. Rappelez-vous que Beñat a sa bille gardée dans sa maison. Alaitz effectue plusieurs opérations sur les deux billes qu'il tient dans ses mains, secouant la boîte d'une manière spéciale. En conséquence de l'enchevêtrement, ces opérations affectent également la bille de Beñat, et Alaitz connaît en outre son influence. Il ouvre donc la boîte pour connaître l'état de ses deux billes. Les billes peuvent être en état GG polluants, GU négociants, UG simultané ou UU. Selon le résultat, Alaitz connaît l'état de la bille de Beñat. Étonnamment, à la suite des opérations d'Alaitz, ces situations potentielles sont envisagées par G négocier+ b U, à négocier U + bageG négocier, à harceler - G négocier et négocier.

Alors Alaitz, dès qu'il voit ses deux billes, l'appelle Beñat et lui dit comment agite la boîte de sa bille pour obtenir la bille qu'Alaitz veut envoyer. Quantique nous a montré que, sachant comment fouetter la boîte, des quatre situations que nous avons présentées, on peut obtenir l'état original de la bille d'Alaitz. Le processus décrit peut être vu dans la figure 3. À la fin du processus, la bille de démarrage d'Alaitz a été télécommandée chez Beñat !

Figure . Processus de télétransport d'une bille entre Alaitz et Beñat. Ed. Gorka Azkune

Est-ce le télétransport quantique le télétransport de nos rêves?

La réponse courte à cette question est négative. Selon la physique actuelle, vous ne pouvez pas obtenir quelque chose comme le télétransport de Star Trek. Pourquoi ? Quelles sont les différences entre le télétransport quantique que nous venons de voir et celui de Star Trek ?

1. Entre Alaitz et Beñat, les billes ne se sont jamais déplacées: L'état de la bille initiale d'Alaitz a été copié à la bille de Beñat, mais il n'y a eu aucun transport de matière.

2. Le téléportage quantique n'est pas instantané. Pour que le télétransport se produise, Alaitz doit informer Beñat de la situation de ses deux billes par téléphone, courrier électronique ou en criant. Cette communication peut se produire à la vitesse maximale de la lumière mais pas à la vitesse. Par conséquent, le télérapport quantique a besoin d'un temps pour être réalisé et ne peut pas dépasser la vitesse de la lumière.

Malgré les problèmes, il semble qu'au moins théoriquement, nous puissions faire téléporter une personne. Mais attention aux difficultés techniques :

1. Pour porter une bille de télétravail, il faut en avoir une autre à l'arrivée (bille de Beñat). Par conséquent, nous devons avoir d'autres particules dans le but de la personne que nous voulons téléporter.

2. Les opérations et mesures devraient être effectuées en tenant compte de toutes les propriétés des particules d'une personne. Dans le cas des billes, nous avons seulement mentionné la couleur, mais les particules quantiques ont de nombreuses propriétés.

3. Nous devrions envoyer toutes les informations de ces millions de mesures à destination en utilisant les canaux de communication habituels.

C'est juste le début. En Quantique, on a déjà vu qu'il est très difficile de maintenir le noeud entre deux particules, qui doivent être isolées du monde. Par conséquent, même s'il n'est pas méprisé, nous pouvons considérer presque impossible qu'une personne puisse se téléporter. De plus, et en passant à un domaine plus philosophique, est-ce la même personne que nous avons téléporté ainsi? En bref, nous avons copié l'information d'une personne à d'autres particules de matière. Nous laissons la question dans l'air.

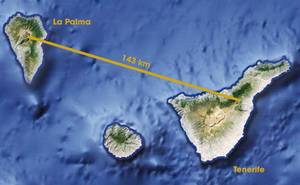
Cependant, la technologie actuelle a déjà permis de transporter des photons et des atomes. Dans le cas des photons, on a obtenu la télé-libéralisation entre les îles de Tenerife et La Palma, imposant un record de 143 km (voir figure 4). Les explications de cette expérience ont été publiées dans la prestigieuse revue Nature en 2012. En 2009, des chercheurs de l'Université du Maryland ont réussi à téléporter un atome à une courte distance.

Télétransport aujourd'hui et demain

Figure . Expérience de télétransport dans les îles Canaries. Ed. Google earth

Nous maîtrisons le télétransport quantique au niveau théorique: on connaît les propriétés de celui-ci, on sait comment le faire et on connaît ses limites. Technologiquement, des mesures très importantes ont également été prises, comme nous l'avons expliqué. Nous sommes convaincus qu'à l'avenir nous pourrons téléporter de plus longues distances et de plus grandes quantités d'informations, mais où est la limite ? Qui sait.

Le rapport quantique sera une technologie très importante à l'avenir. Indispensable dans la cryptographie quantique, ce sera l'une des clés à l'avenir pour l'obtention d'ordinateurs quantiques. Il sera certainement utilisé dans des applications que nous ne pouvons pas imaginer maintenant, qui n'existait en principe que dans le domaine de la fiction.

En Euskal Herria, nous avons l'honneur d'être un groupe de chercheurs de premier plan sur ces sujets. Le groupe Quantum Technologies for Information Science1, du Dr Enrique Solano, venu de la main d'Ikerbasque à Leioa, jouit déjà d'un grand prestige international. L'article publié dans la revue Nature en 2010 en est un exemple.

Ici et là, les chercheurs nous apporteront une nouvelle connaissance de notre monde fascinant. Le rapport quantique nous ouvre de nouvelles portes, mais personne ne peut savoir ce qui va être derrière elles. Comme le dit Pierre Michael Etxenike, la nouvelle connaissance augmente la méconnaissance, car chaque réponse soulève mille nouvelles questions.

Gorka Azkune Galparsoro

Ed. © Iñigo Ibáñez

(Azpeitia, 1982). Il a étudié le génie informatique à l'UPV. Le projet de fin de carrière a été réalisé à l'Institut Max Planck de l'optique quantique, sous la direction d'Ignacio Cirac. Il a travaillé chez Tecnalia dans le domaine de la robotique et de l'intelligence artificielle, et travaille actuellement comme chercheur chez Deusto Tech pour approfondir la recherche dans le domaine des systèmes intelligents dans le but de réaliser une thèse de doctorat.

Bibliographie Bibliographie