Sobre l'estereoscopi

1995/04/01 Bandres Unanue, Luis Iturria: Elhuyar aldizkaria

• Fisika

Per què els objectes que veiem semblen cossos i no figures planes? Encara que la imatge que apareix en la retina dels nostres ulls és plana, què passa perquè vegem els objectes en tres dimensions?

En aquest problema intervenen diferents factors. D'una banda, el diferent grau de lluminositat que reben les diferents parts dels objectes ens aporta la idea de l'aparença. D'altra banda, atès que les diferents parts d'un cos es troben a diferents distàncies del nostre ull, perquè nosaltres tinguem una imatge clara, l'ull ha de fer un treball d'adaptació, per la qual cosa atès que aquesta adaptació es realitza respecte a un punt del cos, respecte a una distància, és a dir, mentre veiem aquest punt completament net, la resta, d'alguna manera, el veurem borrós produint una sensació de relleu.

No obstant això, el factor de major importància en aquest procés és que la imatge que ens dóna cada ull sobre un mateix objecte és diferent. Per a comprovar-ho n'hi ha prou amb mirar un objecte que tenim al nostre costat, primer amb l'ull dret tancat amb l'esquerre i després amb el contrari. La imatge que ens dóna l'ull dret és diferent de la de l'esquerra i fan aparèixer en el nostre cervell la idea del relleu.

Ara agafarem en una pàgina d'un sol objecte, per tant, en un pla, dues imatges dibuixades, una com l'objecte real que veu l'ull esquerre i una altra com el que veu el dret. En aquestes imatges, si cada ull només veu la imatge corresponent, en lloc de veure dues figures planes veurem un objecte convex. Aquestes parelles de dibuixos s'observen mitjançant un dispositiu especial anomenat estereoscopi. En els estereoscopis antics la unió de les imatges s'obtenia mitjançant miralls, mentre que en els actuals s'utilitzen prismes convexos. Per tant, encara que la idea bàsica d'estereoscòpia és molt comuna, el que s'aconsegueix és realment sorprenent.

Estereoscopi natural

No obstant això, les imatges estereoscòpiques poden veure's sense l'ajuda de cap aparell. Per a això només és necessari realitzar una correcció especial dels ulls. El resultat obtingut és equivalent al que obtindríem amb l'aparell (sense augmentar, clar, perquè els estereoscopis aprofitem també per a augmentar la imatge). L'inventor de l'estereoscopi, Wheatston, va utilitzar inicialment la via natural.

A continuació seguirem una sèrie de dibuixos estereoscòpics, cada vegada més difícils i sense cap mena d'ajuda, que ens permeten mirar en directe. Cal fer alguns intents d'èxit.

Comencem per aquests dos punts negres de la imatge. Dirigirem la vista al buit que hi ha entre tots dos, sense moure's i durant uns segons; mentrestant, farem l'esforç com si volguéssim veure un objecte que està darrere del dibuix. Els punts que veurem en breu no seran dos, sinó quatre, que es produiran. Finalment, mentre els punts externs s'allunyen, els interns aniran acostant-se per a unir-se.

Una vegada aconseguit això, fem el mateix amb la següent parella d'imatges:

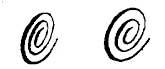
Una vegada aconseguida la suma d'ambdues, estem disposats a fer-ho amb la següent parella:

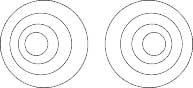
En aquesta última unificació veurem alguna cosa com l'interior d'una canonada la sortida de la qual està lluny.

Una vegada obtingut això, com hem dit, si observem aquesta altra figura, veurem les figures geomètriques com si estiguessin suspeses en l'aire.

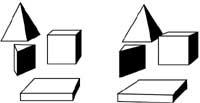
O aquest ens donarà la imatge interior d'un túnel llarg.

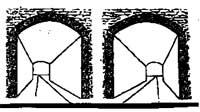
Veure aquestes parelles d'imatges tal com s'ha indicat no sol ser molt difícil. Les persones amb miop i vista cansada no han de retirar les ulleres i han de fer-ho com si miressin qualsevol altra imatge. No obstant això, convé allunyar o acostar el dibuix fins a aconseguir la distància òptima de la imatge. Tots aquests intents han de realitzar-se amb bona claredat i no dedicar-los massa temps perquè no es cansin els ulls.

Vista de gegants

Quan un objecte està molt lluny de nosaltres (a més de 450 m), la distància entre els nostres ulls no pot produir dues imatges diferents en els nostres dos ulls. Per això, les cases remotes, les muntanyes o els paisatges ens semblen plans, i tots els cossos del cel estan a la mateixa distància, encara que la Lluna estigui molt més a prop que el planeta i aquests més que les estrelles.

Per tant, amb objectes de més de 450 m d'altura, perdem la capacitat de detectar directament el relleu.

Aquests objectes són iguals per als nostres dos ulls, ja que la distància entre ells de 6 cm és molt petita comparada amb 450 m. Per això, a l'ésser les fotos estereoscòpiques obtingudes en aquestes condicions iguals, no s'aconsegueix cap sensació de relleu en l'estereoscopi.

Però això té una solució senzilla: als objectes llunyans cal fotografiar-los des de dos punts que disten més de la distància que separa els nostres ulls. En mirar aquestes dues fotos alhora a través de l'estereoscopi, veurem les coses com si la distància entre els nostres ulls fos molt major del normal.

Aquesta és la cua de les fotos estereoscòpiques dels paisatges. En la majoria dels casos els veiem amb prismes d'ampliació i l'efecte obtingut és sorprenent.

Basant-nos en tot això, podem aconseguir el mateix efecte que amb la càmera de fotos utilitzant la “ulleres estereoscòpiques”. Aquests estan formats per dos tubs situats a una distància major a la qual separa els nostres ulls. La imatge que pren cada tub, després de passar per diversos prismes, arriba als nostres ulls. La sensació que es percep en mirar amb aquestes ulleres és impressionant: les muntanyes llunyanes adquireixen relleu, les roques, les cases i els vaixells es veuen en l'espai i no com si estiguessin en una pantalla plana. Així veurien els nostres paisatges els grans gegants.

Aquest tipus d'ulleres solen ser utilitzades pels mariners, els artileros i els agrícolistas i generalment porten una escala de mesurament de distàncies (telemetro estereoscòpic). Els prismàtics habituals que utilitzem nosaltres mateixos sovint, amb una distància entre objectius major que entre els nostres ulls, donen un efecte estereoscòpic.