Errorea "h"-z ala "h"-rik gabe?

Hizkuntza batzuetan ahoskatzen ez bada ere, "h"-ak edozein hizkuntzatan bere funtzioa betetzen du, hitz bat ez baita berdina "h"-z ala "h" gabe. Zerbait haritzea (hari bihurtzea) edo zerbaitetan aritzea ez dira berdinak; zerbait "ahurka" (eskutadaka) izatea edo norbait "aurka" izatea ere ez. Era berean, errorea ere ez da berdina "h"-z ala "h" gabe. Batzuetan "h"-dun hitza eta "h"-rik gabea nahiz eta esanahi ezberdinekoak izan, konektatuta egon daitezke. Ingelesez hear entzutea da eta "h"-a galduz gero, ear , belarri bihurtzen da; nonbait, "h"-a galdu egiten du, entzumenean trabarik egin ez diezaion. Matematiketan "h"-z kalkulatzen den errorea eta "h"-rik gabea ere konektatuta daude, bata zein bestea zuzen egin ez den zerbaiten neurria baitira. "H" hizkiak hitzean hartzen duen tokia ere garrantzitsua da: funtzioa ahurra ala ganbila izan daiteke; haurra, berriz, txintxoa ala alproja. Biderketak duen propietate trukakorragatik matematiketan berdin du "h"-ak errorean zein posizio okupatzen duen, "h"-a dagoen ala ez baita kontua.

Errorearen estimazioa ezberdin errorea

Ekuazio diferentzial bat analitikoki ebazterik ez badago, zenbakizko metodoak erabiliz ebatz daiteke. Emaitza analitikoa zehatza da, zenbakizko metodoaz lortzen den emaitza, ostera, hurbildua da, eta pausoz pauso eraikitzen da. Ekuazio diferentzial bat zenbakizko metodoz askatzean egiten den errorea emaitza zehatzaren eta hurbilduaren arteko diferentzia da. Teorian kenketa bat egitea baino zailtasun gehiagorik ez duen kontzeptua, praktikan kalkulatu behar denean kontzeptu konplexu bilakatzen da. Baina, zein da arazoa? Ekuazio diferentzial askoren emaitza zehatzak ez ditugula ezagutzen. Horregatik, emaitza zehatza ezezaguna zaigunez, ezinezkoa egiten zaigu zenbakizko metodoa erabiltzean egiten ari garen errorea kalkulatzea. Errorea ezagutzen ez badugu ere, badakigu ordena altuko zenbakizko metodoak erabiliz lortzen den emaitza hurbildua ordena baxuagokoekin lortutakoa baino zehatzagoa dena. Hala eta guzti, zenbakizko metodoaz pauso bat ematen den bakoitzean, pauso horretan lortu den emaitza balekoa den ala ez esaten digun neurri bat erabili ohi da. Zein neurri da hau, emaitza zehatza ezagutu ezik errorea ezin dela kalkulatu esan badugu?

Errorearen estimazioa da erabiltzen den neurria. Erabilera handia duen errorearen estimazio bat da ondoz ondoko ordena duten zenbakizko metodoak erabiliz lortzen diren emaitzen diferentzia bezala kalkulatzen dena; ( n+1 ) ordenako zenbakizko metodo bat erabiliz lortzen den emaitzari n ordenakoaz lortzen dena kentzean oinarritzen da, eta estrapolazio lokala izenaz ezagutzen da. Berau darabilgunean, ondoz ondoko ordenako bi metodoz lortutako emaitzen diferentzia aurretiaz ezarri dugun tolerantzia bat baino txikiagoa izatea eskatzen dugu pauso bakoitzean. Baldintza betetzen bada, ( n+1 ) ordenako metodoak emandako emaitza ontzat hartzen da; bestela, pausoko eragiketak errepikatu beharra egongo da eta lehenago erabilitako pausoa baino txikiagoa den beste batekin probatu beharko da. Laborategi batean egin beharreko neurketaren baten estrapolazio lokala erabili nahiko bagenu, doitasun ezberdineko bi aparailu erabiliz neurtu nahi dugun kantitate horren bi neurketa egingo lirateke. Aparailu horien doitasunek ondoz ondokoak izan behar dutenez, doitasun handiagoko aparailua dugunean, bigarren aparailua lehenengoak baino doitasun txikiagoa duten aparailuen artetik doitasun handiena duena izango da. Honela, bata bestearen segidako doitasunak dituzten aparailuak erabiltzen ari garela ziurtatuko genuke. Neurketa bien arteko diferentzia balio jakin bat baino txikiagoa izan arte errepikatu beharko litzateke neurketa, eta, baldintza betez gero, doitasun handiagoko aparailuak emandako emaitza hartuko litzateke ontzat. Laborategiko adibidean argi ikusten denez, emaitza erreala ez ezagutzea kalkulu-kopuruaren bikoizketarekin ordaintzen da.

Honenbestez, estrapolazio lokala baliabide segurua baina aldi berean garestia da. Haren potentziala ordena ezberdineko bi metodorekin lortutako emaitzen konparaketan oinarritzen denez, beti ekarriko du kalkulu-kopuruaren handitzea. Estrapolazio lokalaren ziurtasuna aprobetxatuz eta beronek kalkulu-kopuruan eragingo duen handitzea onartuz, kalkulu-kopuru hau bikoiztera ez iristea posible egin zezaketen metodoen diseinuan zentratu dira zenbakizko metodoen sortzaile edo guraso asko, hau da, ahalik eta ezberdintasun gutxiena izango dituzten ondoz ondoko ordenako bi metodo erditzea izan dute helburu. Alde horretatik, konstante-sorta ezberdin bat eragiketa bakarrean erabilita metodo bat n edo ( n+1 ) ordenakoa egiten duten metodoak oso baliagarriak dira, ondoz ondoko ordena duten bi metodoren arteko ezberdintasuna optimizatzea lortzen baitute. Horren adibide dira txertatutako Runge-Kutta metodoak. Haietan, nahikoa da ( n+1 ) ordenako metodoaz emaitza lortzeko egindako eragiketez gain beste eragiketa bat bakarrik egitea n ordenako metodoak ematen digun emaitza eskura izateko. Ordena bateko eta besteko emaitzak lortzeko aukera merke bat eskaintzen dute, beraz. Aukera hau baino merkeagoa den beste bat bakarrik dago: biak baten prezioan lortzea, alegia. Baina hori ezinezkoa da, metodo ezberdinak zerbaitetan ezberdindu beharko dira eta.

"h"-dun estimazioa ezberdin "h"-rik gabea

Zenbakizko metodoetan, "h" hizkia pausoaren tamaina adierazteko erabili ohi da. Hasierako puntuko emaitza zehatza ezagututa, "h" neurriko pauso bat ematen da eta puntu berri horretan ekuazio diferentzialaren emaitza hurbildua kalkulatzen da, zenbakizko metodoak agintzen dizkigun eragiketak eginez. Puntu berrian lortutako emaitza hurbildua erabiliz prozesua errepikatu egiten da. Pauso bakoitzeko errorea neurtzeko bi motatako estimazioak erabili ohi dira: bata, pauso-unitateko estimazioa deritzona, ondoz ondoko metodoz lortutako emaitzen arteko diferentzia hutsa ("h"-rik gabea); bestea, pausoko estimazioa izenekoa, emaitzen arteko diferentzia pausoaren tamainaz biderkatuta lortzen dena ("h"-duna). Jakina, "h"-dun estimazioa eta "h"-rik gabea ez dira berdinak. Suposatu pauso unitateko errorearen estimazio bat daukagula. Normalean erabiltzen diren pausoen tamainak unitatea baino txikiagoak direnez, estimazio hau "h"-z biderkatuz lortzen den pausoko estimazioa aurretiaz daukaguna baino txikiagoa izango da. Ondorioz, gerta daiteke "h"-z biderkatu gabe ezarritako tolerantzia baino txikiagoa ez den estimazioa "h"-z biderkatu ostean tolerantziaren azpitik egotea, hau da, pausoaren txikitasunak "langa" pasatzen lagundu izana. Horretaz gain, "h"-z biderkatutako estimazioak pauso txikiei abantaila berezia ematen die, estimazioa "h" txikiago batez biderkatzean estimazio berria txikiagoa izango baita. Beste hitz batzuetan esanda, pauso unitateko estimazioak ("h"-rik gabeak) langa altuera berean jartzen die pauso guztiei. "H"-z biderkatuta lortzen den estimazioak, berriz, pauso guztiei langa jaisten die. Pauso txikiak dira langa gehien jaitsi zaienak.

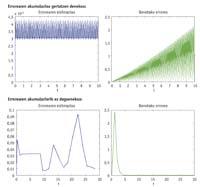
Batzuetan, langa jaisteak ez du eraginik izango, hasieran langak zuen altuera laguntzarik gabe pasatuko luketen estimazioak egongo baitira. Baina egongo dira hasieran langak zuen altuera gainditu ezin duten eta langa jaisteak hura pasaraztea eragingo dien saltariak. Ondorioz, beste estimazio bat erabilita errepikatu beharko litzatekeen pausoa balekotzat emango da. Pauso baten errepikapenak pauso txikiagoekin proba egitea dakar, eta pausoak txikiak badira, gehiagoren beharra egoten da. Beraz, langa jaisten ari gareneko estimazioak erabiltzen ditugunean pauso gutxiago eta, ondorioz, handiagoak emango dira langarik jaisten ez denekoetan baino. Txanponak badu beste alderdi bat ere, ordea, gerta baitaiteke langa jaisteak pausoaren onarpena eragin duen emaitza nahi bezain ona ez izatea. Horrek azken errorean eragin txarra izan dezake, eta lortuko dugun emaitza hurbilduaren kalitatea asko jaitsi daiteke. Oro har, "h"-rik gabe kalkulatzen den estimazioak pauso txikiagoak eta gehiago eman beharra ekarriko du, baina benetako errorearen metaketa ere txikiagoa izango da.

Errorearen estimazioa, "h"-z ala "h"-rik gabe?

Ekuazio diferentzialak zurrunak edo ez-zurrunak izan daitezke. Ekuazio diferentzial zurrunaren definizio praktikoa algoritmo batek pauso asko eman behar dituen ekuazioarena da. "Asko" hitzak zenbaki konkreturik adierazten ez badu ere, 100 pauso ez dira asko, eta 3.000 asko dira. Problema zurruna denean, "h"-rik gabeko estimazioa erabiltzea hobesten da, "h"-dun estimazioarekin lortuko genukeen emaitza baino askoz hobea lortuko baita "h"-rik ez duenarekin. Problema zurruna ez denean ere, "h"-rik gabeko estimazioa erabilita lortuko dugun emaitza "h"-duna erabilita lortzen dena baino hobea izango da gehienetan, baina emaitza --bien arteko ezberdintasuna-- ez da izango hain ikusgarria, hau da, ekuazio diferentzial ez-zurrunetan "h"-rik gabeko estimazioa erabiltzeak dakarren lan gehigarriak ez du emaitzan distira handirik sortuko.

Hizkuntzetan, garaiaren arabera hitz batek "h"-a galtzea edo irabaztea ohikoa da. Horren adibide dira batzuetan "h"-dun edo "h"-rik gabeko hormak eraiki izana, edota "h"-dun edo "h"-rik gabeko ospitaleetan gaixoak sendatu izana. Hala ere, garaiak eraginda "h"-a itsatsi edo kendu zaien hitzen funtzio edo esanahiak berdina izaten jarraitu du. Matematiketan "h"-dun eta "h"-rik gabeko erroreen gaia ez da garaiaren araberakoa: beti egon izan da bien arteko bizikidetza, eta biak dira beharrezko, baten eta bestearen funtzioa sekula ez baita izan berdina. Hitz batek "h"-a duen ala ez hiztegian kontsultatzen dugun bezalaxe, errorearen estimazioan "h"-a erabili ala ez erabakitzeko askatu beharreko problema "kontsultatu" egin beharko da, emaitzan lortuko dugun arrakastaren gakoa hortxe egongo baita: errorearen estimazioak "h"-a izatean edo ez izatean.